I. HÌNH ĐA DIỆN, KHỐI ĐA DIỆN
1. Khái niệm về hình đa diện
Hình đa diện (gọi tắt là đa diện) $(H)$ là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất:
a) Hai đa giác phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác. Mỗi đa giác như thế được gọi là một mặt của hình đa diện $(H).$ Các đỉnh, cạnh của các đa giác ấy theo thứ tự gọi là các đỉnh, cạnh của hình đa diện $(H).$
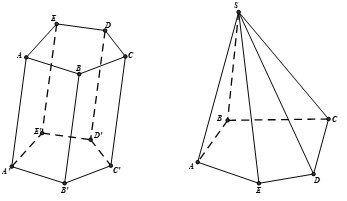
Khối đa diện là phần không gian được giới hạn bới một hình đa diện (H), kể cả hình đa diện đó.
2. Khối đa diện lồi
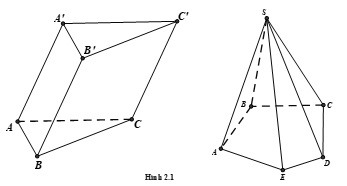
Khối đa diện $\left( H \right)$ được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của $\left( H \right)$ luôn thuộc $\left( H \right).$ Khi đó đa diện giới hạn $\left( H \right)$ được gọi là đa diện lồi (Hình 2.1)
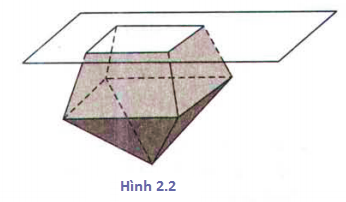
Lưu ý: Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng đi qua một mặt của nó. (Hình 2.2)
Công thức ƠLE: Trong một đa diện lồi nếu gọi \(D\) là số đỉnh, \(C\) là số cạnh, \(M\) là số mặt thì $D - C + M = 2$
3. Khối da diện đều
Khối đa diện đều là khối đa diện lồi có các tính chất sau:
a) Mỗi mặt của nó là một đa giác đều $p$ cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng $q$ mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại $\left\{ {p;q} \right\}.$
Nhận xét: Các mặt của khối đa diện đều là những đa giác đều và bằng nhau.
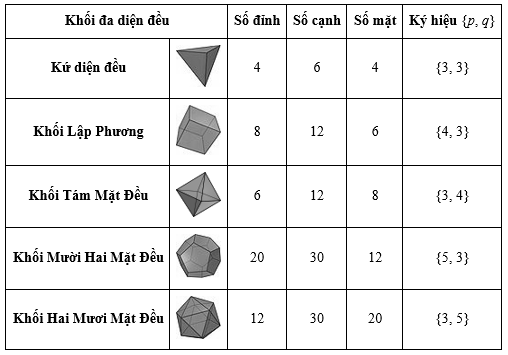
Định lí: Chỉ có năm loại khối đa diện đều. Đó là các khối đa diện đều loại $\left\{ {3,3} \right\},$ loại $\left\{ {4,3} \right\},\;$ loại $\left\{ {3,4} \right\},$ loại $\left\{ {5,3} \right\},$ và loại $\left\{ {3,5} \right\}.$
II. THỂ TÍCH KHỐI ĐA DIỆN
1. Thể tích khối chóp
1) Nếu khối chóp đã cho có chiều cao $h$ và diện tích đáy $B$ thì thể tích tính theo công thức \(V = \dfrac{1}{3}Bh\)
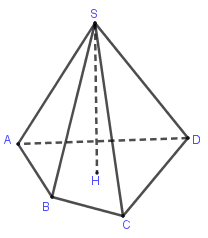
2) Nếu khối chóp cần tính thể tích chưa biết chiều cao thì ta phải xác định được vị trí chân đường cao trên đáy.
a) Chóp có cạnh bên vuông góc chiều cao chính là cạnh bên.
b) Chóp có hai mặt bên vuông góc đáy đường cao là giao tuyến của hai mặt bên vuông góc đáy.
c) Chóp có mặt bên vuông góc đáy chiều cao của mặt bên vuông góc đáy.
d) Chóp đều chiều cao hạ từ đỉnh đến tâm đa giác đáy.
e) Chóp có hình chiếu vuông góc của một đỉnhlên xuống mặt đáy thuộc cạnh mặt đáy đường cao là từ đỉnh tới hình chiếu.
Chú ý: Các công thức tính diện tích đáy
a) Tam giác:
\(S = \dfrac{1}{2}a{h_a} = \dfrac{1}{2}b{h_b} = \dfrac{1}{2}c{h_c}\)
\(S = \dfrac{1}{2}ab\sin C = \dfrac{1}{2}bc\sin A = \dfrac{1}{2}ac\sin B\)
\(S = \dfrac{{abc}}{{4R}};S = pr;\) \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)
\(\Delta ABC\) vuông tại \(A\): \(S = \dfrac{1}{2}AB.AC\)
\(\Delta ABC\) đều cạnh \(a\): \(S = \dfrac{{{a^2}\sqrt 3 }}{4}\)
b) Hình vuông cạnh $a:$ $S = {a^2}$ ($a:$ cạnh hình vuông)
c) Hình chữ nhật: $S = a.b$ ($a,b:$ hai kích thước)
d) Hình bình hành $ABCD:$ $S = $ đáy $ \times $ cao \( = AB.AD.\sin \widehat {BAD}\)
e) Hình thoi $ABCD:$\(S = AB.AD.\sin \widehat {BAD} = \dfrac{1}{2}AC.BD\)
f) Hình thang: \(S = \dfrac{1}{2}\left( {a + b} \right)h\) ($a,b:$ hai đáy, $h:$ chiều cao)
g) Tứ giác $ABCD$ có hai đường chéo vuông góc: \(S = \dfrac{1}{2}AC.BD\)
2. Tỉ số thể tích
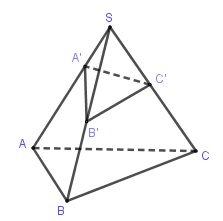
Cho khối chóp $S.ABC,{\rm{ }}A' \in SA,{\rm{ }}B' \in SB,{\rm{ }}C' \in SC$. Khi đó \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\)
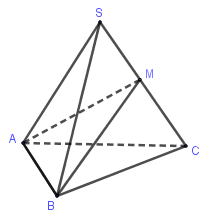
+) Với điểm \(M \in SC\) ta có: \(\dfrac{{{V_{S.ABM}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SC}}\)
3. Thể tích khối lăng trụ
1) Thể tích khối lăng trụ
\(V = B.h\) với $B$ là diện tích đáy, $h$ là chiều cao
2) Thể tích khối hộp chữ nhật
\(V = abc\) với $a,b,c$ là ba kích thước
3) Thể tích khối lập phương
\(V = {a^3}\) với $a$ là độ dài cạnh

