Bài viết trình bày dạng hàm số bậc bốn trùng phương và các bước khảo sát hàm số.
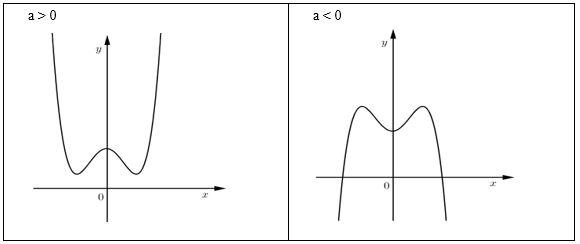
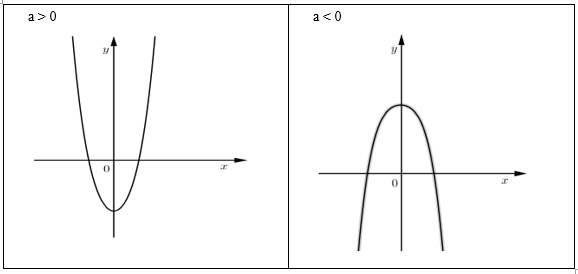
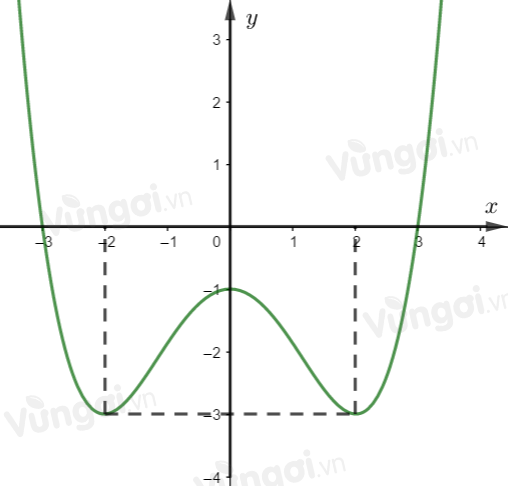
Hàm số bậc bốn trùng phương \(y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)\)
+) TXĐ: $D = R$
+) Sự biến thiên:
\(\begin{array}{l}y' = 4a{x^3} + 2bx\\y' = 0 \Leftrightarrow 4a{x^3} + 2bx = 0 \Leftrightarrow 2x\left( {2a{x^2} + b} \right) = 0 \Leftrightarrow x = ..\\\mathop {\lim }\limits_{x \to - \infty } y;\,\mathop {\lim }\limits_{x \to + \infty } y\end{array}\)
+) Đồ thị:
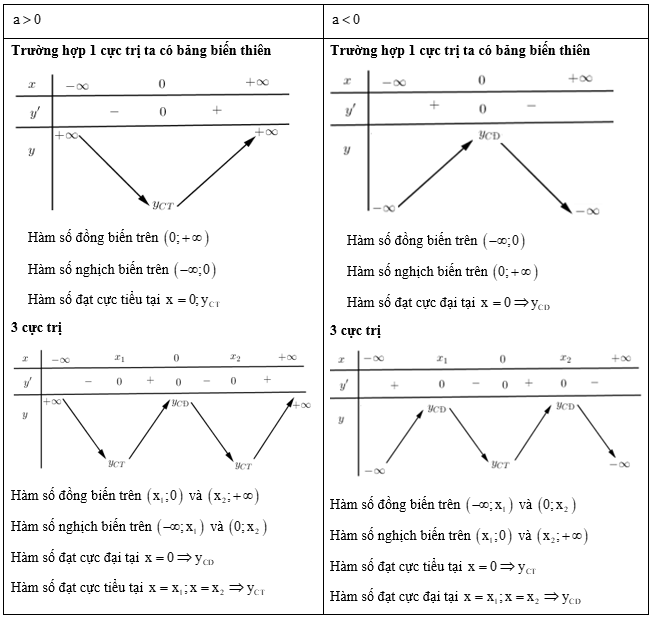
TH1: \(y' = 0\) có 3 nghiệm phân biệt \( \Leftrightarrow ab < 0\)
TH2: \(y' = 0\) chỉ có một nghiệm \( \Leftrightarrow \left[ \begin{array}{l}ab > 0\\b = 0\end{array} \right.\)
