1. Các kiến thức cần nhớ
Định nghĩa:
- Hàm số lũy thừa là hàm số có dạng \(y = {x^\alpha }\left( {\alpha \in R} \right)\).
- Tập xác định:
+ \(\alpha \) nguyên dương: \(D = R\).
+ \(\alpha \) nguyên âm hoặc \(\alpha = 0\): \(D = R\backslash \left\{ 0 \right\}\).
+ \(\alpha \) không nguyên: \(D = \left( {0; + \infty } \right)\).
Chú ý:
\(\sqrt[n]{x} = {x^{\frac{1}{n}}} \Leftrightarrow x > 0\). Ngoài ra hai hàm số \(y = \sqrt[n]{x}\) và \(y = {x^{\frac{1}{n}}}\left( {n \in {N^*}} \right)\) là không đồng nhất vì có tập xác định khác nhau.
Đạo hàm:
\(\left( {{x^\alpha }} \right)' = \alpha {x^{\alpha - 1}};{u^\alpha }\left( x \right)' = \alpha u'\left( x \right){u^{\alpha - 1}}\left( x \right)\)
\(\left( {\sqrt[n]{x}} \right)' = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}};\left( {\sqrt[n]{{u\left( x \right)}}} \right)' = \dfrac{{u'\left( x \right)}}{{n\sqrt[n]{{{u^{n - 1}}\left( x \right)}}}}\)
+ Nếu \(x > 0\) thì \(\sqrt[n]{x} = {x^{\frac{1}{n}}}\) nên \(\left( {\sqrt[n]{x}} \right)' = ({x^{\frac{1}{n}}})' = \dfrac{1}{n}{x^{ - \frac{n - 1}{n}}} = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}\)
+ Nếu \(x \le 0\) thì đẳng thức trên không xảy ra.
Khảo sát hàm số \(y = {x^\alpha }\left( {\alpha \ne 0} \right)\) trên tập \(\left( {0; + \infty } \right)\).
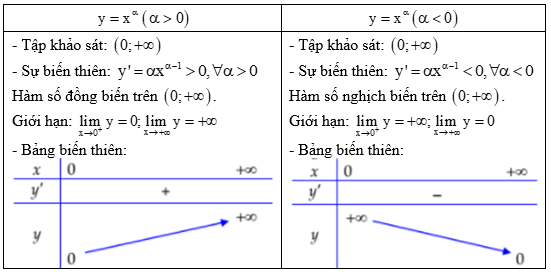
- Đồ thị:
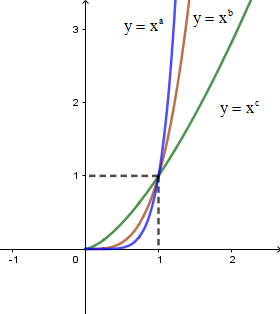
Luôn đi qua điểm \(\left( {1;1} \right)\)

- Trên đây ta chỉ xét chung các hàm số trên tập \(\left( {0; + \infty } \right)\). Thực tế tập xác định của mỗi hàm số là khác nhau phụ thuộc vào điều kiện của \(\alpha \).
- Tránh nhầm lẫn tập \(\left( {0; + \infty } \right)\) là tập xác định cho mọi hàm số lũy thừa.
2. Một số dạng toán thường gặp
Dạng 1: Tìm tập xác định của hàm số.
Phương pháp:
- Bước 1: Xác định số mũ \(\alpha \) của hàm số.
- Bước 2: Nêu điều kiện để hàm số xác định.
+ \(\alpha \) nguyên dương: \(D = R\).
+ \(\alpha \) nguyên âm hoặc \(\alpha = 0\): \(D = R\backslash \left\{ 0 \right\}\).
+ \(\alpha \) không nguyên: \(D = \left( {0; + \infty } \right)\).
- Bước 3: Giải các bất phương trình ở trên để tìm tập xác định của hàm số.
Dạng 2: Tính đạo hàm của hàm số.
Phương pháp:
- Bước 1: Áp dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương để tính đạo hàm hàm số đã cho.
\(\left( {u \pm v} \right)' = u' \pm v';\left( {uv} \right)' = u'v + uv';\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\)
- Bước 2: Tính đạo hàm các hàm số thành phần dựa vào công thức tính đạo hàm các hàm số cơ bản: hàm đa thức, phân thức, hàm mũ, logarit, lũy thừa,…
- Bước 3: Tính toán và kết luận.
Dạng 3: Tìm mỗi quan hệ của các số mũ của các hàm số lũy thừa khi biết đồ thị của chúng.
Phương pháp:
Quan sát đồ thị hàm số và nhận xét tính đồng biến, nghịch biến và các điểm đi qua để suy ra tính chất của các số mũ.