Cho hình vẽ sau:
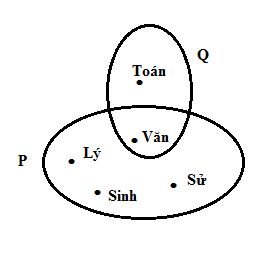
Viết tập hợp P và Q.
Ta có: P = {Lý, Văn, Sinh, Sử}; Q = {Toán, Văn}.
Cho hình vẽ sau:
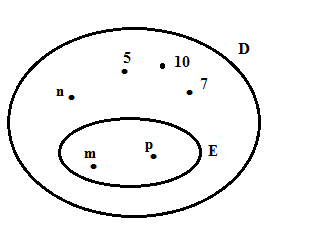
Viết tập hợp D và E.
Ta có: \(D = \left\{ {m;n;p;5;10;7} \right\}\) và \(E = \left\{ {m,p} \right\}\).
Cho C={x | x là số tự nhiên chia cho 3 dư 1, 3 < x < 18}. Hãy viết tập hợp C bằng cách liệt kê các phần tử của tập hợp.
Các số tự nhiên chia 3 dư 1 lớn hơn 3 và nhỏ hơn 18 là: $4; 7; 10; 13; 16$.
$ =>C = \left\{4; 7; 10; 13; 16\right\}$
Viết tập hợp \(C\) gồm các phần tử thuộc \(A\) nhưng không thuộc \(B.\)
Các phần tử thuộc A nhưng không thuộc B là \(1;2\)
Nên \(C = \left\{ {1;2} \right\}.\)
Cho A là tập hợp các số tự nhiên nhỏ hơn 7, hình nào sau đây biểu diễn tập hợp A?
Các số tự nhiên nhỏ hơn 7 là 0;1;2;3;4;5;6.
Các số trong hình quả trứng chỉ có thể là 7 số trên.
Số tự nhiên từ 7 trở lên phải nằm bên ngoài hình quả trứng.
B sai vì thiếu phần tử 3
C sai vì 7 không thuộc A.
D sai vì phần tử 6 kí hiệu 2 lần.
Viết tập hợp gồm tất cả các phần tử vừa thuộc tập hợp \(A\) vừa thuộc tập hợp \(B.\)
Các phần tử thuộc cả A và B là \(3;4\).
Nên tập hợp thỏa mãn là \(\left\{ {3;4} \right\}.\)
Cho H là tập hợp các tháng dương lịch có đúng 30 ngày. Phần tử của H là?
Tháng 1 và tháng 3 có 31 ngày nên loại A, C
Tháng 2 có 28 hoặc 29 ngày nên loại B.
Tháng 4 có 30 ngày.
Cho tập hợp B là tập hợp các số chẵn nhỏ hơn 10. Số nào sau đây không là phần tử của tập hợp B?
Số 14 là số lớn hơn 10 nên 14 không là phần tử của B.
Viết tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10.\)
Tập hợp A các số tự nhiên lớn hơn \(5\) và nhỏ hơn \(10\) là \(A = \left\{ {6;7;8;9} \right\}.\)
Viết tập hợp \(P\) các chữ cái khác nhau trong cụm từ: “ HOC SINH”
Các chữ cái khác nhau trong cụm từ “ HOC SINH” là H;O;C;S;I;N
Nên \(P = \left\{ {H;O;C;S;I;N} \right\}.\)
Viết tập hợp \(A = \left\{ {16;17;18;19} \right\}\) dưới dạng chỉ ra tính chất đặc trưng.
Nhận thấy các số \(16;17;18;19\) là các số tự nhiên lớn hơn \(15\) và nhỏ hơn \(20\)
Nên \(A = \left\{ {x \in N |15 < x < 20} \right\}\).
Số phần tử của tập hợp \(P\) gồm các chữ cái trong cụm từ “ WORLD CUP” là
Các chữ cái trong cụm từ “ WORLD CUP” là W;O;R;L;D;C;U; P.
Nên tập hợp P={W;O;R;L;D;C;U; P} bao gồm \(8\) phần tử.
Cho hình vẽ.
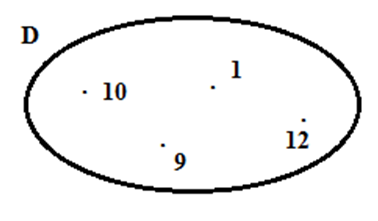
Tập hợp \(D\) là
Ta có các số trong vòng tròn là \(1,9,10,12\) nên tập hợp \(D = \left\{ {1;9;10;12} \right\}\).
Số phần tử của tập hợp các số tự nhiên lẻ lớn hơn \(10\) nhỏ hơn \(50\) là
Các số tự nhiên lẻ lớn hơn \(10\) và nhỏ hơn \(50\) là \(11;13;15;...;47;49.\)
Nên có \(\left( {49 - 11} \right):2 + 1 = 20\) số tự nhiên lẻ lớn hơn \(10\) và nhỏ hơn \(50\).
Vậy số phần tử của tập hợp các số tự nhiên lẻ lớn hơn \(10\) nhỏ hơn \(50\) là \(20.\)
Viết tập hợp $A = \{ x|22 < x \le 27\} $ dưới dạng liệt kê các phần tử ta được:
Các số lớn hơn \(22\) và nhỏ hơn hoặc bằng \(27\) là \(23;24;25;26;27.\)
Nên \(A = \left\{ {23;24;25;26;27} \right\}.\)
Tập hợp \(P\) gồm các số tự nhiên lớn hơn \(50\) và không lớn hơn \(57\). Kết luận nào sau đây là sai?
Các số tự nhiên lớn hơn \(50\) và không lớn hơn \(57\) là \(51;52;53;54;55;56;57\)
Nên \(P = \left\{ {51;52;53;54;55;56;57} \right\}\)
Do đó \(58 \notin P\) nên D sai.
Cho hình vẽ sau:
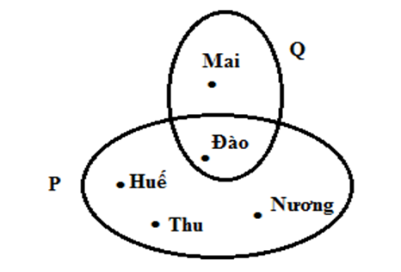
Viết tập hợp P và Q.
Ta có P={Huế; Thu; Nương; Đào}
Q={Đào; Mai}
Cho hình vẽ sau:
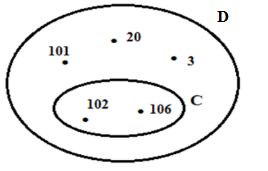
Viết tập hợp C và D.
\(C = \left\{ {102;106} \right\}\) và \(D = \left\{ {3;20;101;102;106} \right\}\)
Cho B là tập hợp các số tự nhiên nhỏ hơn 10. Trong các khẳng định sau, có bao nhiêu khẳng định sai?
1. \(2 \in B\)
2. \(5 \notin B\)
3. \(B = \left\{ {0;1;2;3;4;5;6;7;8;9;10} \right\}\)
4. \(B = \left\{ {9;8;7;6;5;4;3;2;1;0} \right\}\)
5. \(B = \left\{ {0;1;1;2;3;4;5;6;7;8;9} \right\}\)
Số 2 là số tự nhiên nhỏ hơn 10 nên \(2 \in B\) =>Khẳng định 1 đúng.
Số 5 là số tự nhiên nhỏ hơn 10 nên \(5 \in B\) =>Khẳng định 2 sai.
Tập hợp B là tập hợp các số tự nhiên nhỏ hơn 10 nên các phần tử của B là:
1;2;3;4;5;6;7;8;9
\( \Rightarrow B = \left\{ {1;2;3;4;5;6;7;8;9} \right\}\)\( = \left\{ {9;8;7;6;5;4;3;2;1} \right\}\) =>Khẳng định 4 đúng.
Tập hợp B trong khẳng định 3 có chứa số 10 mà 10 không thuộc B =>Khẳng định 3 sai.
\(B = \left\{ {1;1;2;3;4;5;6;7;8;9} \right\}\) có số 1 được liệt kê hai lần => Khẳng định 5 sai
Vậy có 3 khẳng định sai.

