Bài tập ôn tập chương 7

- Tâm đối xứng của đoạn thẳng AB là trung điểm của đoạn thẳng AB.

- Tam giác đều ABC không có tâm đối xứng

- Tâm đối xứng của đường tròn tâm O là điểm O.

Vậy (1) và (3) là hình có tâm đối xứng

- Trục đối xứng của đoạn thẳng AB là đường thẳng đi qua trung điểm của đoạn thẳng AB và vuông góc với nó.

- Trục đối xứng của tam giác đều ABC là đường thẳng đi qua một đỉnh và trung điểm của cạnh đối diện đỉnh đó.

- Trục đối xứng của đường tròn tâm O là đường thẳng đi qua điểm O.

Vậy (1), (2), (3) là hình có trục đối xứng.

Tam giác đều có 3 trục đối xứng => A sai

Hình chữ nhật với hai kích thước khác nhau có 2 trục đối xứng => B sai

Hình thang cân, góc ở đáy khác \({90^0}\) , có một đúng một trục đối xứng => C đúng

Hình bình hành không có trục đối xứng => D sai

Các câu A, B, D đúng.

Hình lục giác đều có 6 trục đối xứng gồm 3 đường thẳng đi qua hai định đổi diện và 3 đường thẳng đi qua trung điểm của hai cạnh đối diện => C sai.

Độ dài đoạn OA là: \(4:2 = 2\left( {cm} \right)\)    

Các câu A, B, C đúng

Câu D sai vì chữ I vừa có tâm đối xứng vùa có trục đối xứng

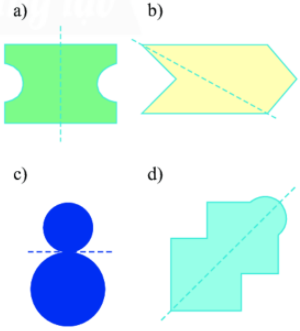
Đường nét đứt ở hình a và d là trục đối xứng. Hai đường ở hình b và c còn lại không phải là trục đối xứng của hình

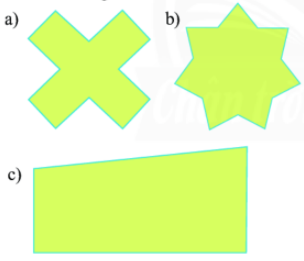
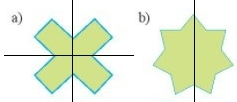
Hình a và hình b có trục đối xứng, ví dụ ta có thể vẽ trục đối xứng của chúng như sau:

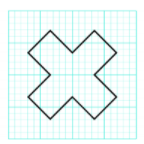
Ta vẽ các trục đối xứng của hình như sau:

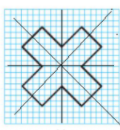
Vậy hình đã cho có 4 trục đối xứng.

Phép tính Toàn quan sát được là:

\({\bf{89}} + {\bf{16}} + {\bf{69}} + {\bf{61}} + {\bf{98}} + {\bf{11}}{\rm{ }} = {\bf{344}} \)

Phép tính Na quan sát được là:

\({\bf{11}} + {\bf{86}} + {\bf{19}} + {\bf{69}} + {\bf{91}} + {\bf{68}}{\rm{ }} = {\bf{344}} \)