Các dạng toán về phân số với tử số và mẫu số là số nguyên

+) \(\dfrac{{12}}{0}\) không là phân số vì mẫu số bằng $0.$

+) \(\dfrac{3}{{0,25}}\) không là phân số vì mẫu số là số thập phân.

+) \(\dfrac{{4,4}}{{11,5}}\) không là phân số vì tử số và mẫu số là số thập phân.

+) \(\dfrac{{ - 4}}{5}\) là phân số vì \( - 4;\,5\, \in \mathbb{Z} \) và mẫu số là $5$ khác $0.$

Trong hình có \(2\) ô vuông tô màu và tổng tất cả \(8\) ô vuông nên phân số biểu thị là \(\dfrac{2}{8} = \dfrac{1}{4}\)

\(\begin{array}{l}\dfrac{{35}}{{15}} = \dfrac{x}{3}\\35.3 = 15.x\\x = \dfrac{{35.3}}{{15}}\\x = 7\end{array}\)

Vậy \(x = 7\)

Các phân số thỏa mãn bài toán là:

$\dfrac{1}{{ - 2}},\dfrac{3}{{ - 2}},\dfrac{4}{{ - 2}},\dfrac{{ - 2}}{1},\dfrac{{ - 2}}{3},\dfrac{{ - 2}}{4}$

Vậy có tất cả \(6\) phân số.

- Các phân số dương: \(\dfrac{{15}}{{60}};\dfrac{6}{{15}};\dfrac{3}{{12}}\)

+ Vì \(15.15 \ne 60.6\) nên \(\dfrac{{15}}{{60}} \ne \dfrac{6}{{15}}\)

+ Vì \(6.12 \ne 15.3\) nên \(\dfrac{6}{{15}} \ne \dfrac{3}{{12}}\)

+ Vì \(15.12 = 60.3\) nên \(\dfrac{{15}}{{60}} = \dfrac{3}{{12}}\)

- Các phân số âm: \(\dfrac{{ - 7}}{5};\dfrac{{28}}{{ - 20}}\)

Vì \(\left( { - 7} \right).\left( { - 20} \right) = 5.28\) nên \(\dfrac{{ - 7}}{5} = \dfrac{{28}}{{ - 20}}\)

Vậy có hai cặp phân số bằng nhau trong các phân số đã cho.

Vì \(C \in N\) nên \(C \in Z.\) Do đó ta tìm \(n \in Z\) để \(C \in Z\)

Vì \(n \in Z\) nên để \(C \in Z\) thì \(2n + 1 \in U\left( {11} \right) = \left\{ { \pm 1; \pm 11} \right\}\)

Ta có bảng:

Vì \(C \in N\) nên ta chỉ nhận các giá trị \(n = 0;n = 5\)

Vì \(n\) nguyên dương nên để \(\dfrac{9}{{4n + 1}}\) nguyên thì \(4n + 1 \in U\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\)

Ta có bảng:

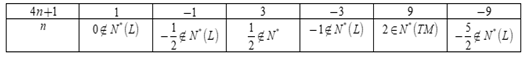
Vậy có duy nhất một giá trị của \(n\) thỏa mãn là \(n = 2\)

Ta có: \(\dfrac{6}{9} = \dfrac{{12}}{a} \Rightarrow 6.a = 9.12\) \( \Rightarrow a = \dfrac{{9.12}}{6} = 18\)

\(\dfrac{6}{9} = \dfrac{b}{{ - 54}} \Rightarrow 6.\left( { - 54} \right) = 9.b\) \( \Rightarrow b = \dfrac{{6.\left( { - 54} \right)}}{9} =  - 36\)

\(\dfrac{6}{9} = \dfrac{{ - 738}}{c} \Rightarrow 6.c = 9.\left( { - 738} \right)\) \( \Rightarrow c = \dfrac{{9.\left( { - 738} \right)}}{6} =  - 1107\)

Vậy \(a + b + c\) \( = 18 + \left( { - 36} \right) + \left( { - 1107} \right) =  - 1125\)

Ta có:

\(A = \dfrac{{3n - 5}}{{n + 4}} = \dfrac{{3n + 12 - 12 - 5}}{{n + 4}}\)\( = \dfrac{{3\left( {n + 4} \right) + \left( { - 17} \right)}}{{n + 4}}\) \( = \dfrac{{3\left( {n + 4} \right)}}{{n + 4}} + \dfrac{{ - 17}}{{n + 4}} = 3 + \dfrac{{ - 17}}{{n + 4}}\)

Vì \(n \in Z\) nên để \(A \in Z\) thì \(n + 4 \in U\left( { - 17} \right) = \left\{ { \pm 1; \pm 17} \right\}\)

Ta có bảng:

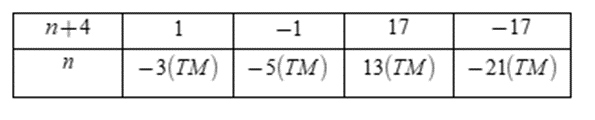
Vậy \(n \in \left\{ { - 21; - 5; - 3;13} \right\}\)

Ta có: \(\dfrac{x}{5} = \dfrac{3}{y}\)\( \Rightarrow x.y = 5.3 = 15\)

Mà \(15 = 5.3 = 15.1 = \left( { - 3} \right).\left( { - 5} \right) = \left( { - 1} \right).\left( { - 15} \right)\) và \(x,y \in Z,x > y\) nên \(\left( {x;y} \right) \in \left\{ {\left( {5;3} \right),\left( {15;1} \right),\left( { - 3; - 5} \right),\left( { - 1; - 15} \right)} \right\}\)

Ta có: \(x - y = 5 \Rightarrow x = y + 5\) thay vào \(\dfrac{{x - 4}}{{y - 3}} = \dfrac{4}{3}\) ta được:

\(\begin{array}{l}\dfrac{{y + 5 - 4}}{{y - 3}} = \dfrac{4}{3}\\\dfrac{{y + 1}}{{y - 3}} = \dfrac{4}{3}\\3\left( {y + 1} \right) = 4\left( {y - 3} \right)\\3y + 3 = 4y - 12\\3y - 4y =  - 12 - 3\\ - y =  - 15\\y = 15\\ \Rightarrow x = 15 + 5 = 20\end{array}\)

Vậy \(x = 20;y = 15\)

\(\begin{array}{l}\dfrac{x}{3} = \dfrac{{27}}{x}\\x.x = 81\\{x^2} = 81\end{array}\)

Ta có: \(x = 9\) hoặc \(x =  - 9\)

Kết hợp điều kiện \(x < 0\) nên có một giá trị \(x\) thỏa mãn là: \(x =  - 9\)

Viết số nguyên \( - 16\) dưới dạng phân số ta được: \(\dfrac{{ - 16}}{1}\)

Phân số \(\dfrac{{ - 9}}{7}\) được đọc là: Âm chín phần bảy