Các dạng toán về số nguyên tố, hợp số, phân tích một số ra thừa số nguyên tố

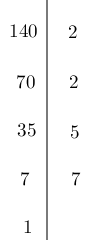
Suy ra $140 = {2^2}.5.7 = {a^2}.b.7$ nên \(a = 2\).

Ta có ${\rm{150 = 2}}{\rm{.3}}{\rm{.}}{{\rm{5}}^2}$, vậy $x = 1;y = 1;z = 2$

Vậy số lượng ước của số $150$  là $\left( {1 + 1} \right)\left( {1 + 1} \right)\left( {2 + 1} \right) = 2.2.3 = 12$

+) Phân tích số \(2150\) thành thừa số nguyên tố

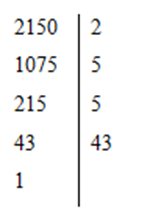
Suy ra \(2150 = {2.5^2}.43\)

+) Phân tích số \(1490\) thành thừa số nguyên tố

Suy ra \(1490 = 2.5.149\)

+) Phân tích số \(2340\) thành thừa số nguyên tố

Suy ra \(2340 = {2^2}{.3^2}.5.13\)

Vậy có số \(2340\) thỏa mãn yêu cầu đề bài.

A. Đáp án này đúng vì mọi số tự nhiên đều có ước chung là $1$.

B. Đáp án này sai, vì $0$ không là ước của $1$ số nào cả.

C. Đáp án này sai, vì số nguyên tố có $2$ ước là $1$ và chính nó.

D. Đáp án này sai, vì $2$ số nguyên tố có ước chung là $1$.

Gọi hai số tự nhiên cần tìm là \(a\) và \(b\left( {a;b \in N} \right)\)

Ta có \(a.b = 105\)

Phân tích số \(105\) ra thừa số nguyên tố ta được \(105 = 3.5.7\)

Các số \(a;b\) là ước của \(105\) , do đó ta có

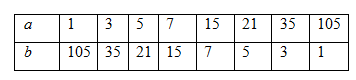
Vậy có \(8\) cặp số thỏa mãn yêu cầu.

Tổng $3$ số nguyên tố là $578$ là số chẵn, nên trong $3$ số nguyên tố có ít nhất $1$ số là số chẵn. Ta đã biết số $2$ là số nguyên tố chẵn duy nhất. Vậy số nguyên tố nhỏ nhất trong $3$ số nguyên tố có tổng là $578$ là số $2.$

Ta có

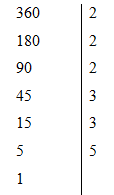
Nên \(360 = {2^3}{.3^2}.5\)

Vậy có  thừa số nguyên tố sau khi phân tích là $2; 3$ và $5.$

Các số \(x\) thỏa mãn \(50 < x < 60\) là \(51;52;53;54;55;56;57;58;59\)

Trong đó các số nguyên tố là \(53;59.\)

Vậy có hai số nguyên tố thỏa mãn đề bài.

Ta có \({n^2} + 12n = n\left( {n + 12} \right);\,n + 12 > 1\) nên để \({n^2} + 12n\) là số nguyên tố thì \(n = 1.\)

Thử lại \({n^2} + 12n = {1^2} + 12.1 = 13\) (nguyên tố)

Vậy với \(n = 1\) thì \({n^2} + 12n\) là số nguyên tố.

Đặt \(p = 3a + r\,\,\left( {r = 0;1;2;\,a \in N} \right)\)

Với \(r = 1\) ta có \(p + 8 = 3a + r + 8 = \left( {3a + 9} \right) \vdots 3,\,\left( {3a + 9} \right) > 3\) nên \(p + 8\) là hợp số. Do đó loại \(r = 1.\)

Với \(r = 2\) ta có \(p + 4 = 3a + r + 4 = \left( {3a + 6} \right) \vdots 3,\,\left( {3a + 6} \right) > 3\) nên \(p + 4\) là hợp số. Do đó loại \(r = 2.\)

Do đó \(r = 0;p = 3a\) là số nguyên tố nên \(a = 1 \Rightarrow p = 3.\)

Ta có \(p + 4 = 7;p + 8 = 11\) là các số nguyên tố.

Vậy \(p = 3.\)

Có một số nguyên tố \(p\) thỏa mãn đề bài.

Ta có \(p = 42.a + r = 2.3.7.a + r\,\left( {a,r \in N;0 < r < 42} \right)\)

Vì \(p\) là số nguyên tố nên \(r\) không chia hết cho \(2;3;7.\)

Các hợp số nhỏ hơn \(42\) không chia hết cho \(2\) là \(9;15;21;25;27;33;35;39\)

Loại bỏ các số chia hết cho \(3\) và \(7\) ta còn số \(25.\)

Vậy \(r = 25.\)

Nếu xếp 7 hình vuông đơn vị thành hình chữ nhật thì chiều rộng của hình chữ nhật chỉ có thể xếp:

Các số nguyên tố nhỏ hơn 30 là:  2;3;5;7;9;11;13;17;19;23;29.

Số cần tìm là 23.

91 có tổng các chữ số bằng 10 không chia hết cho 3 nên 3 không là ước nguyên tố của 91

91 có chữ số tận cùng là 1 nên 91 không chia hết cho 2, do đó 2 không là ước nguyên tố.

Một ước số nguyên tố của 91 là: 7.

Ta có

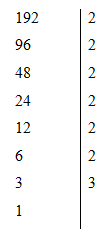
Nên \(192= 2^6 . 3\) nên số ước của $192$ là \((6+1)(1+1)=14\) ước.

Phân tích số \(1936\) ra thừa số nguyên tố ta được

Hay \(1936 = {2^4}{.11^2} = \left( {{2^2}.11} \right).\left( {{2^2}.11} \right) = 44.44\)

Vậy cạnh hình vuông bằng \(44\,m.\)

Vì \(\overline {ab} .\,c\, = 424\) nên \(\overline {ab} \) là ước có hai chữ số của \(424.\)

Phân tích số \(424\) ra thừa số nguyên tố ta được

Hay \(424 = {2^3}.53\)

Các ước của \(424\) là \(1;2;4;8;53;106;212;424\)

Suy ra \(\overline {ab}  = 53\) suy ra \(c = 424:53 = 8.\)

Vậy \(40 = 2.2.2.5 = {2^3}.5\)

\(400 = {2^4}{.5^2}\)

\(800 = 400.2 = {2.2^4}{.5^2} = {2^5}{.5^2}\)

Số 225 chia hết cho các số nguyên tố: 3; 5

Vậy 225 chia hết cho 2 số nguyên tố.