Các bài toán về mặt phẳng và mặt cầu
Kỳ thi ĐGNL ĐHQG Hồ Chí Minh
Trong không gian \(Oxyz\), cho đường thẳng \(\Delta :\,\,\dfrac{{x - 1}}{{ - 2}} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\) và mặt phẳng \(\left( P \right):\,\,2x - y + z - 3 = 0\). Gọi \(\left( S \right)\) là mặt cầu có tâm \(I\) thuộc \(\Delta \) và tiếp xúc với \(\left( P \right)\) tại điểm \(H\left( {1; - 1;0} \right)\). Phương trình của \(\left( S \right)\) là:
Vì \(I \in \Delta :\,\,\dfrac{{x - 1}}{{ - 2}} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\) nên ta gọi \(I\left( {1 - 2t;\,\,2t;\,\,2 + t} \right)\).
Vì \(\left( S \right)\) tiếp xúc với \(\left( P \right):\,\,2x - y + z - 3 = 0\) tại điểm \(H\left( {1; - 1;0} \right)\) nên ta có: \(d\left( {I;\left( P \right)} \right) = IH = R\).
\(\begin{array}{l} \Leftrightarrow \dfrac{{\left| {2.\left( {1 - 2t} \right) - 2t + 2 + t - 3} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \sqrt {{{\left( {2t} \right)}^2} + {{\left( { - 1 - 2t} \right)}^2} + {{\left( { - 2 - t} \right)}^2}} \\ \Leftrightarrow \dfrac{{\left| { - 5t + 1} \right|}}{{\sqrt 6 }} = \sqrt {9{t^2} + 8t + 5} \\ \Leftrightarrow 25{t^2} - 10t + 1 = 54{t^2} + 48t + 30\\ \Leftrightarrow 29{t^2} + 58t + 29 = 0\\ \Leftrightarrow {t^2} + 2t + 1 = 0\\ \Leftrightarrow {\left( {t + 1} \right)^2} = 0\\ \Leftrightarrow t = - 1\end{array}\)
\( \Rightarrow I\left( {3; - 2;1} \right)\) và \(R = IH = \sqrt 6 \).
Vậy phương trình mặt cầu \(\left( S \right)\) là: \({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 1} \right)^2} = 6\).
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {z^2} - 8x + 2y + 2z - 3 = 0\) và đường thẳng \(\Delta :\,\,\dfrac{{x - 1}}{3} = \dfrac{y}{{ - 2}} = \dfrac{{z + 2}}{{ - 1}}\). Mặt phẳng \(\left( \alpha \right)\) vuông góc với \(\Delta \) và cắt \(\left( S \right)\) theo giao tuyến là đường tròn \(\left( C \right)\) có bán kính lớn nhất. Phương trình \(\left( \alpha \right)\) là:
Đường thẳng \(\Delta :\,\,\dfrac{{x - 1}}{3} = \dfrac{y}{{ - 2}} = \dfrac{{z + 2}}{{ - 1}}\) có 1 VTCP là \(\overrightarrow u = \left( {3; - 2; - 1} \right)\).
Vì \(\left( \alpha \right) \bot \Delta \) nên mặt phẳng \(\left( \alpha \right)\) có 1 VTPT là \(\overrightarrow n = \overrightarrow u = \left( {3; - 2; - 1} \right)\). Khi đó phương trình mặt phẳng \(\left( \alpha \right)\) có dạng \(3x - 2y - z + d = 0\).
Mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {z^2} - 8x + 2y + 2z - 3 = 0\) có tâm \(I\left( {4; - 1; - 1} \right)\), bán kính \(R = \sqrt {16 + 1 + 1 + 3} = \sqrt {21} \).
Gọi \(r\) là bán kính đường tròn \(\left( C \right)\), \(d = d\left( {I;\left( \alpha \right)} \right)\).
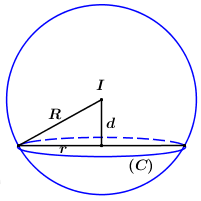
Áp dụng định lí Pytago ta có: \({R^2} = {r^2} + {d^2}\), do đó để \(r\) đạt GTLN thì \(d\) phải đạt GTNN (vì \(R = \sqrt {21} \) không đổi).
Ta có: \(d = \dfrac{{\left| {3.4 - 2.\left( { - 1} \right) - 1.\left( { - 1} \right) + d} \right|}}{{\sqrt {{3^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{{\left| {15 + d} \right|}}{{\sqrt {14} }} \ge 0\), suy ra \({d_{\min }} = 0 \Leftrightarrow d = - 15\).
Vậy phương trình mặt phẳng \(\left( \alpha \right)\) cần tìm là: \(3x - 2y - z - 15 = 0\).
