Các bài toán về đường thẳng và mặt phẳng

Gọi \(I\left( {a;b;c} \right)\) là điểm thỏa mãn đẳng thức : \(2\overrightarrow {IA}  + 3\overrightarrow {IB}  = \overrightarrow 0 \)

\(\begin{array}{l} \Rightarrow 2\left( {2 - a; - 2 - b;4 - c} \right) + 3\left( { - 3 - a;3 - b; - 1 - c} \right) = \overrightarrow 0 \\ \Rightarrow \left\{ \begin{array}{l}4 - 2a - 9 - 3a = 0\\ - 4 - 2b + 9 - 3b = 0\\8 - 2c - 3 - 3c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 5a - 5 = 0\\ - 5b + 5 = 0\\ - 5c + 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 1\\c = 1\end{array} \right. \Rightarrow I\left( { - 1;\;1;\;1} \right)\end{array}\)

Ta có :

\(\begin{array}{l}2M{A^2} + 3M{B^2} = 2{\overrightarrow {MA} ^2} + 3{\overrightarrow {MB} ^2}\\ = 2{\left( {\overrightarrow {MI}  + \overrightarrow {IA} } \right)^2} + 3{\left( {\overrightarrow {MI}  + \overrightarrow {IB} } \right)^2}\\ = 5M{I^2} + \left( {2I{A^2} + 3I{B^2}} \right) + \overrightarrow {MI} \left( {2\overrightarrow {IA}  + 3\overrightarrow {IB} } \right)\\ = 5M{I^2} + \left( {2I{A^2} + 3I{B^2}} \right)\end{array}\)

Do I, A, B cố định nên \(2I{A^2} + 3I{B^2} = const\).

 \( \Rightarrow {\left( {2M{A^2} + 3M{B^2}} \right)_{\min }} \Leftrightarrow 5M{I^2}_{\min }\)\( \Leftrightarrow \) M là hình chiếu của I trên (P)

Gọi \(\left( \Delta  \right)\) là đường thẳng đi qua I vuông góc với (P) , ta có phương trình của \(\left( \Delta  \right):\left\{ \begin{array}{l}x =  - 1 + 2t\\y = 1 - t\\z = 1 + 2t\end{array} \right.\).

M là hình chiếu của I lên (P) \( \Rightarrow M \in \left( \Delta  \right) \Rightarrow M\left( { - 1 + 2t;1 - t;1 + 2t} \right)\) .

Lại có \(M \in \left( P \right)\)  

\(\begin{array}{l} \Rightarrow 2\left( { - 1 + 2t} \right) - \left( {1 - t} \right) + 2\left( {1 + 2t} \right) - 8 = 0\\ \Leftrightarrow  - 2 + 4t - 1 + t + 2 + 4t - 8 = 0\\ \Leftrightarrow 9t - 9 = 0 \Leftrightarrow t = 1 \Rightarrow M\left( {1;0;3} \right)\end{array}\)

Khi đó ta có

\(\begin{array}{l}M{I^2} = 4 + 1 + 4 = 9;\;\;\;I{A^2} = 9 + 9 + 9 = 27;\;\;\;I{B^2} = 4 + 4 + 4 = 13\\ \Rightarrow {\left( {2M{A^2} + 3M{B^2}} \right)_{\min }} = 5.9 + 2.27 + 3.12 = 135\end{array}\)

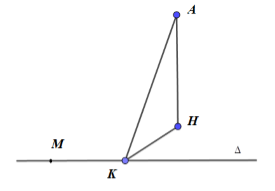
Do \(\Delta \) là đường thẳng đi qua \(M\left( {0;0;2} \right)\) và song song với mặt phẳng \(\left( P \right):x + y + z + 3 = 0\) \( \Rightarrow \Delta  \subset \left( Q \right)\): qua M và song song \(\left( P \right)\).

Phương trình mặt phẳng (Q) là: \(x + y + z - 2 = 0\).

Dựng \(AH \bot \left( Q \right),AK \bot \Delta \). Ta có: \(AK \ge AH\). Do đó, khoảng cách từ \(A\left( {5;0;0} \right)\) đến đường thẳng \(\Delta \) nhỏ nhất và bằng AH khi và chỉ khi K trùng H

Khi đó, đường thẳng \(\Delta \) được xác định là đường thẳng đi qua M và H.

Phương trình đường thẳng AH là \(\left\{ \begin{array}{l}x = 5 + t\\y = t\\z = t\end{array} \right. \Rightarrow \)Giả sử \(H\left( {5 + t;t;t} \right) \Rightarrow 5 + t + t + t - 2 = 0 \Leftrightarrow t =  - 1 \Rightarrow H\left( {4; - 1; - 1} \right)\)

\( \Rightarrow \overrightarrow {MH}  = \left( {4; - 1; - 3} \right) \Rightarrow \Delta \) có 1 VTCP là \(\overrightarrow {{u_3}}  = \left( {4; - 1; - 3} \right)\).

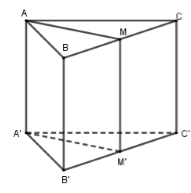
Phương trình \(BC \equiv Oz:\left\{ \begin{array}{l}x = 0\\y = 0\\z = t\end{array} \right.\).

Mặt phẳng \(\left( {AMM'A'} \right)\) đi qua \(A'\) và vuông góc với \(BC\) nên \(\left( {AMM'A'} \right)\) đi qua \(A'\left( {\sqrt 3 ; - 1;1} \right)\) và nhận \(\overrightarrow k  = \left( {0;0;1} \right)\) làm VTPT hay \(\left( {AMM'A'} \right):0\left( {x - \sqrt 3 } \right) + 0\left( {y + 1} \right) + 1\left( {z - 1} \right) = 0 \Leftrightarrow z = 1\).

\(M = BC \cap \left( {AMM'A'} \right) \Rightarrow t - 1 = 0 \Leftrightarrow t = 1 \Rightarrow M\left( {0;0;1} \right)\)

Mà \(AA' = 1,A'M = \sqrt {{{\left( {\sqrt 3  - 0} \right)}^2} + {{\left( { - 1 - 0} \right)}^2} + {{\left( {1 - 1} \right)}^2}}  = 2\) \( \Rightarrow AM = \sqrt {A'{M^2} - A'{A^2}}  = \sqrt {{2^2} - {1^2}}  = \sqrt 3 \).

Tam giác \(ABC\) đều có độ dài đường cao \(AM = \dfrac{{BC\sqrt 3 }}{2} = \sqrt 3  \Rightarrow BC = 2\)

Gọi \(B\left( {0;0;m} \right),C\left( {0;0;n} \right)\) với \(n \ne 0\) thì \(BC = 2 \Leftrightarrow \left| {m - n} \right| = 2\) và \(M\left( {0;0;1} \right)\) là trung điểm \(BC \Leftrightarrow \dfrac{{m + n}}{2} = 1 \Leftrightarrow m + n = 2\).

Khi đó \(m = 0,n = 2\) vì \(n \ne 0\) hay \(C\left( {0;0;2} \right)\).

\( \Rightarrow \overrightarrow {A'C}  = \left( { - \sqrt 3 ;1;1} \right)\) hay \(2\overrightarrow {AC'}  = \left( { - 2\sqrt 3 ;2;2} \right)\) là một VTCP của \(A'C\).

Suy ra \(a =  - 2\sqrt 3 ,b = 2 \Rightarrow {a^2} + {b^2} = {\left( { - 2\sqrt 3 } \right)^2} + {2^2} = 16\).

Gọi \(N = d \cap \Delta \). Giả sử \(N\left( {2 - 2t;\,\,8 + t;\,\,t} \right) \Rightarrow \overrightarrow {MN}  = \left( { - 2t;\,\,7 + t;\,\,t - 1} \right)\).

Đường thẳng \(\Delta :\,\,\dfrac{{x - 2}}{{ - 2}} = \dfrac{{y - 8}}{1} = \dfrac{z}{1}\) có 1 VTCP là \(\overrightarrow {{u_\Delta }}  = \left( { - 2;1;1} \right)\), đường thẳng \(d\) nhận \(\overrightarrow {MN} \) là 1 VTPT.

Do \(d \bot \Delta \) nên \(\overrightarrow {MN} .\overrightarrow {{u_\Delta }}  = 0\).

\(\begin{array}{l} \Leftrightarrow  - 2t.\left( { - 2} \right) + \left( {7 + t} \right).1 + \left( {t - 1} \right).1 = 0\\ \Leftrightarrow 6t + 6 = 0 \Leftrightarrow t =  - 1\\ \Rightarrow \overrightarrow {MN}  = \left( {2;6; - 2} \right)\end{array}\)

\( \Rightarrow \) Đường thẳng \(d\) đi qua \(M\left( {2;1;1} \right)\) và có 1 VTCP \(\overrightarrow {{u_d}}  = \dfrac{1}{2}\overrightarrow {MN}  = \left( {1;3; - 1} \right)\) có phương trình là: \(\left\{ \begin{array}{l}x = 2 + t'\\y = 1 + 3t'\\z = 1 - t'\end{array} \right.\).

Khi đó, giao điểm của \(d\) và mặt phẳng \(\left( {Oyz} \right)\) ứng với \(t'\) thỏa mãn \(x = 2 + t' = 0 \Leftrightarrow t' =  - 2\).

\( \Rightarrow \) Tọa độ giao điểm của \(d\) và mặt phẳng \(\left( {Oyz} \right)\) là: \(\left( {0; - 5;3} \right)\).

Gọi \(M = d \cap {\Delta _1} \Rightarrow M\left( {1 + {t_1};\,\, - 2 + 4{t_1};\,\,2 + 3{t_1}} \right)\), \(N = d \cap {\Delta _2} \Rightarrow N\left( { - 4 + 5{t_2};\,\, - 7 + 9{t_2};\,\,{t_2}} \right)\).

\( \Rightarrow \overrightarrow {MN}  = \left( {5{t_2} - {t_1} - 5;\,\,9{t_2} - 4{t_1} - 5;\,\,{t_2} - 3{t_1} - 2} \right)\).

Vì \(d \bot \left( P \right):\,\,4y - z + 3 = 0\) có 1 VTPT là \(\overrightarrow n \left( {0;4; - 1} \right)\) nên \(\overrightarrow {MN} \) và \(\overrightarrow n \) là 2 vectơ cùng phương.

\( \Rightarrow \overrightarrow {MN}  = k\overrightarrow n \,\,\left( {k \ne 0} \right)\)\( \Leftrightarrow \left\{ \begin{array}{l}5{t_2} - {t_1} - 5 = 0\\9{t_2} - 4{t_1} - 5 = 4k\\{t_2} - 3{t_1} - 2 =  - k\end{array} \right.\)  \( \Leftrightarrow \left\{ \begin{array}{l}{t_1} = 5{t_2} - 5\\9{t_2} - 4{t_1} - 5 = 4k\\4{t_2} - 12{t_1} - 8 =  - 4k\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}{t_1} = 5{t_2} - 5\\13{t_2} - 16{t_1} - 13 = 0\\{t_2} - 3{t_1} - 2 =  - k\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{t_1} = 5{t_2} - 5\\13{t_2} - 16\left( {5{t_2} - 5} \right) - 13 = 0\\{t_2} - 3{t_1} - 2 =  - k\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{t_1} = 5{t_2} - 5\\ - 67{t_2} + 67 = 0\\{t_2} - 3{t_1} - 2 =  - k\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{t_2} = 1\\{t_1} = 0\\k = 1\end{array} \right.\) .

\( \Rightarrow M\left( {1;\,\, - 2;\,\,2} \right),\,\,N\left( {1;\,\,2;\,\,1} \right)\) \( \Rightarrow \overrightarrow {MN}  = \left( {0;4; - 1} \right)\).

Vậy phương trình đường thẳng \(d\) đi qua \(M\) và có 1 VTCP \(\overrightarrow {MN} \left( {0;4; - 1} \right)\) là: \(\left\{ \begin{array}{l}x = 1\\y =  - 2 + 4t\\z = 2 - t\end{array} \right.\)

Vì \(M \in d:\,\,\dfrac{x}{{ - 2}} = \dfrac{{y - 1}}{1} = \dfrac{z}{1} \Rightarrow \) Gọi \(M\left( { - 2t;\,\,1 + t;\,\,t} \right)\).

Ta có: \(OM = \sqrt {{{\left( { - 2t} \right)}^2} + {{\left( {1 + t} \right)}^2} + {t^2}}  = \sqrt {6{t^2} + 2t + 1} \).

\(d\left( {M;\left( P \right)} \right) = \dfrac{{\left| {2\left( { - 2t} \right) - \left( {1 + t} \right) + 2t - 2} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {2^2}} }} = \dfrac{{\left| { - 3t - 3} \right|}}{3} = \left| {t + 1} \right|\).

Theo bài ra ta có: M cách đều gốc tọa độ O và mặt phẳng \(\left( P \right)\)\( \Leftrightarrow \sqrt {6{t^2} + 2t + 1}  = \left| {t + 1} \right|\).

\(\begin{array}{l} \Leftrightarrow 6{t^2} + 2t + 1 = {t^2} + 2t + 1\\ \Leftrightarrow 5{t^2} = 0 \Leftrightarrow t = 0\end{array}\)

\( \Rightarrow M\left( {0;1;0} \right)\)

Vậy có 1 điểm \(M\)  thỏa mãn yêu cầu bài toán là \(M\left( {0;1;0} \right)\).

Ta có \(A\left( {4; - 3;5} \right),B\left( {2; - 5;1} \right)\) nên trung điểm của AB là \(I\left( {3; - 4;3} \right)\).

Đường thẳng \(\left( d \right):\dfrac{{x + 1}}{3} = \dfrac{{y - 5}}{{ - 2}} = \dfrac{{z + 9}}{{13}}\) có 1 VTCP là \(\overrightarrow {{u_d}}  = \left( {3; - 2;13} \right)\).

Mặt phẳng \(\left( P \right)\) vuông góc với d  nên mặt phẳng (P) có 1 VTPT \(\overrightarrow {{n_P}}  = \overrightarrow {{u_d}}  = \left( {3; - 2;13} \right)\).

Mặt phẳng \(\left( P \right)\) có vectơ pháp tuyến là \(\overrightarrow n  = \left( {3; - 2;13} \right)\) và đi qua \(I\left( {3; - 4;3} \right)\) có phương trình là:

\(3\left( {x - 3} \right) - 2\left( {y + 4} \right) + 13\left( {z - 3} \right) = 0\)\( \Leftrightarrow 3x - 2y + 13z - 56 = 0\).

Gọi \(d\) là đường thẳng đi qua \(M\left( { - 1;3;2} \right)\) và vuông góc với mặt phẳng \(\left( P \right):\,\,x - 2y + 4z + 1 = 0\).

\( \Rightarrow \overrightarrow {{u_d}}  = \overrightarrow {{n_P}}  = \left( {1; - 2;4} \right)\).

\( \Rightarrow \) Phương trình đường thẳng là: \(\dfrac{{x + 1}}{1} = \dfrac{{y - 3}}{{ - 2}} = \dfrac{{z - 2}}{4}\).