Các trường hợp bằng nhau của tam giác vuông
Sách kết nối tri thức với cuộc sống
Cho tam giác ABC có AB < AC. Cho M là trung điểm của cạnh BC. Tia phân giác của góc A cắt đường thẳng qua M, vuông góc với BC tại điểm I. Qua I kẻ IH vuông góc với AB, IK vuông góc với AC ( H \( \in \) đường thẳng AB, K \( \in \) đường thẳng AC). Phát biểu nào sau đây sai:
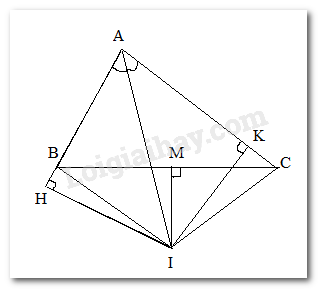
Xét tam giác vuông AIH và AIK có:
AI chung
\(\widehat {HAI} = \widehat {KAI}\) ( do AI là tia phân giác của góc BAC)
\( \Rightarrow \Delta AIH = \Delta AIK\) ( cạnh huyền – góc nhọn)
\( \Rightarrow \) AH = AK ; IH = IK ( các cạnh tương ứng) nên A đúng
Xét tam giác vuông MBI và MCI có:
MB = MC ( do M là trung điểm của BC)
\(\widehat {BMI} = \widehat {CMI}( = 90^\circ )\)
MI chung
\( \Rightarrow \)\(\Delta MBI = \Delta MCI\) ( c.g.c)
\( \Rightarrow \) BI = CI ( 2 cạnh tương ứng)
Xét tam giác vuông HBI và KCI có:
BI = CI ( cmt)
HI = KI ( cmt)
\( \Rightarrow \)\(\Delta HBI = \Delta KCI\) ( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \) HB = KC ( 2 cạnh tương ứng) nên D đúng
Ta có:
AB + AC = (AH – HB) + (AK + KC) = AK – KC + AK + KC = 2.AK ( vì AH = AK, HB = KC)
\( \Rightarrow AK = \frac{{AB + AC}}{2}\) nên B đúng
Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của tia \(BC\) lấy điểm \(M,\) trên tia đối của tia \(CB\) lấy điểm \(N\) sao cho \(MB = NC.\) Kẻ \(BE \bot AM\,\left( {E \in AM} \right);CF \bot AN\,\left( {F \in AN} \right)\).
Tam giác \(AMN\) là tam giác gì?
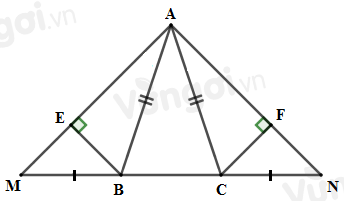
\(\Delta ABC\) cân tại \(A\) nên \(AB = AC,\,\widehat {ABC} = \widehat {ACB}\) (1)
Mặt khác: \(\widehat {ABM} + \widehat {ABC} = {180^o}\) (kề bù) (2)
\(\widehat {ACN} + \widehat {ACB} = {180^o}\) (kề bù) (3)
Từ (1), (2) và (3) suy ra \(\widehat {ABM} = \widehat {ACN}\).
Xét \(\Delta ABM\) và \(\Delta ACN\) có:
\(AB = AC\,\,(cmt)\)
\(\widehat {ABM} = \widehat {ACN}\,\,(cmt)\)
\(BM = CN\,\,(gt)\)
\( \Rightarrow \Delta ABM = \Delta ACN\,\,(c.g.c)\)
\( \Rightarrow AM = AN\) (hai cạnh tương ứng).
\( \Rightarrow \Delta AMN\) cân tại \(A.\)
Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của tia \(BC\) lấy điểm \(M,\) trên tia đối của tia \(CB\) lấy điểm \(N\) sao cho \(MB = NC.\) Kẻ \(BE \bot AM\,\left( {E \in AM} \right);CF \bot AN\,\left( {F \in AN} \right)\).
So sánh \(BE\) và \(CF.\)
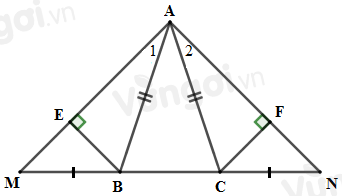
Sử dụng kết quả câu trước ta có \(\Delta ABM = \Delta ACN\,\,\) suy ra \(\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng).
Xét hai tam giác vuông \(ABE\) và \(ACF\) có:
\(\widehat {AEB} = \widehat {AFC} = {90^o}\)
\(AB = AC\) (vì \(\Delta ABC\) cân tại \(A\))
\(\widehat {{A_1}} = \widehat {{A_2}}\,\,(cmt)\)
\( \Rightarrow \Delta ABE = \Delta ACF\) (cạnh huyền – góc nhọn)
\( \Rightarrow BE = CF\) (hai cạnh tương ứng).
Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của tia \(BC\) lấy điểm \(M,\) trên tia đối của tia \(CB\) lấy điểm \(N\) sao cho \(MB = NC.\) Kẻ \(BE \bot AM\,\left( {E \in AM} \right);CF \bot AN\,\left( {F \in AN} \right)\).
Chọn câu đúng.
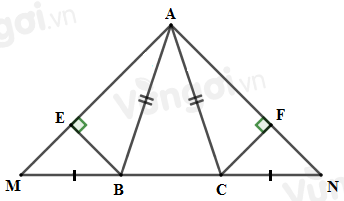
Sử dụng kết quả câu trước \(\Delta ABE = \Delta ACF\) nên \(BE = CF\) (hai cạnh tương ứng).
Xét hai tam giác vuông \(BME\) và \(CNF\) có:
\(\widehat {BEM} = \widehat {CFN} = {90^o}\)
\(BE = CF\,\,(cmt)\)
\(MB = NC\,\,(gt)\)
\( \Rightarrow \Delta BME = \Delta CNF\) (cạnh huyền – cạnh góc vuông).

