Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của tia \(BC\) lấy điểm \(M,\) trên tia đối của tia \(CB\) lấy điểm \(N\) sao cho \(MB = NC.\) Kẻ \(BE \bot AM\,\left( {E \in AM} \right);CF \bot AN\,\left( {F \in AN} \right)\).
So sánh \(BE\) và \(CF.\)
Trả lời bởi giáo viên
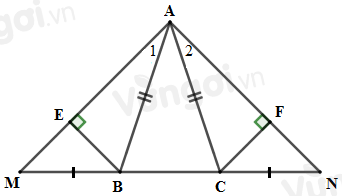
Sử dụng kết quả câu trước ta có \(\Delta ABM = \Delta ACN\,\,\) suy ra \(\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng).
Xét hai tam giác vuông \(ABE\) và \(ACF\) có:
\(\widehat {AEB} = \widehat {AFC} = {90^o}\)
\(AB = AC\) (vì \(\Delta ABC\) cân tại \(A\))
\(\widehat {{A_1}} = \widehat {{A_2}}\,\,(cmt)\)
\( \Rightarrow \Delta ABE = \Delta ACF\) (cạnh huyền – góc nhọn)
\( \Rightarrow BE = CF\) (hai cạnh tương ứng).
Hướng dẫn giải:
- Chứng minh \(\Delta ABE = \Delta ACF\) (cạnh huyền – góc nhọn) từ đó suy ra hai cạnh tương ứng bằng nhau.

