Cho tam giác ABC có AB < AC. Cho M là trung điểm của cạnh BC. Tia phân giác của góc A cắt đường thẳng qua M, vuông góc với BC tại điểm I. Qua I kẻ IH vuông góc với AB, IK vuông góc với AC ( H \( \in \) đường thẳng AB, K \( \in \) đường thẳng AC). Phát biểu nào sau đây sai:
Trả lời bởi giáo viên
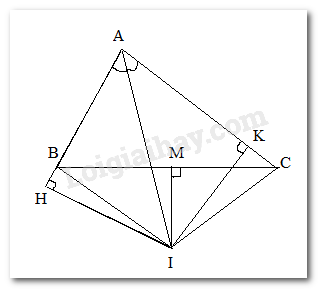
Xét tam giác vuông AIH và AIK có:
AI chung
\(\widehat {HAI} = \widehat {KAI}\) ( do AI là tia phân giác của góc BAC)
\( \Rightarrow \Delta AIH = \Delta AIK\) ( cạnh huyền – góc nhọn)
\( \Rightarrow \) AH = AK ; IH = IK ( các cạnh tương ứng) nên A đúng
Xét tam giác vuông MBI và MCI có:
MB = MC ( do M là trung điểm của BC)
\(\widehat {BMI} = \widehat {CMI}( = 90^\circ )\)
MI chung
\( \Rightarrow \)\(\Delta MBI = \Delta MCI\) ( c.g.c)
\( \Rightarrow \) BI = CI ( 2 cạnh tương ứng)
Xét tam giác vuông HBI và KCI có:
BI = CI ( cmt)
HI = KI ( cmt)
\( \Rightarrow \)\(\Delta HBI = \Delta KCI\) ( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \) HB = KC ( 2 cạnh tương ứng) nên D đúng
Ta có:
AB + AC = (AH – HB) + (AK + KC) = AK – KC + AK + KC = 2.AK ( vì AH = AK, HB = KC)
\( \Rightarrow AK = \frac{{AB + AC}}{2}\) nên B đúng
Hướng dẫn giải:
Từ các trường hợp bằng nhau của tam giác vuông suy ra cặp cạnh tương ứng bằng nhau
Cộng, trừ đoạn thẳng suy ra các đẳng thức

