Kết quả:
0/32
Thời gian làm bài: 00:00:00
Bậc của đơn thức \(\left( { - \dfrac{1}{3}x{z^2}} \right)by\left( { - \dfrac{2}{5}xyz} \right)\) (với \(b\) là hằng số) là
Trong các biểu thức sau, biểu thức nào là đơn thức?
Một tam giác cân có góc ở đỉnh bằng \({64^0}\) thì số đo góc ở đáy là:
Cho tam giác \(ABC\) cân tại \(A\) có \(AM\) là đường trung tuyến khi đó
Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác.
Cho \(p\left( x \right) = 5{x^4} + 4{x^3} - 3{x^2} + 2x - 1\) và \(q\left( x \right) = - {x^4} + 2{x^3} - 3{x^2} + 4x - 5.\)
Tính \(p\left( x \right) + q\left( x \right)\) rồi tìm bậc của đa thức thu được.
Cho đa thức sau : \(f(x) = 2{x^2} + \,12x + 10\). Trong các số sau, số nào là nghiệm của đa thức đã cho:
Chọn đáp án đúng. Cho tam giác \(ABC\) có đường cao \(AH\) . Biết \(B\) nằm giữa \(H\) và \(C.\) Ta có:
Cho $\Delta ABC$ vuông tại $A,$ ${\rm{ }}AH \bot BC{\rm{ }}(H \in BC);AB{\rm{ }} = 9cm,$${\rm{ }}AH = 7,2cm,{\rm{ }}HC = 9,6cm.$
Tính cạnh $AC;BC.$
Cho \(f\left( x \right) = {x^5} - 3{x^4} + {x^2} - 5\) và \(g\left( x \right) = 2{x^4} + 7{x^3} - {x^2} + 6.\) Tìm hiệu \(f\left( x \right) - g\left( x \right)\) rồi sắp xếp kết quả theo lũy thừa tăng dần của biến ta được:
Có bao nhiêu đơn thức trong các biểu thức sau \( - x\dfrac{2}{5}{y^2}{x^2};\,2 + x{y^3};{\left( { - x} \right)^3}6y;xy^2z;\dfrac{{xyz}}{{x - 1}}\) ?
Trong các biểu thức đại số sau, biểu thức nào không phải đơn thức?
Cho tam giác $ABC$ và tam giác $DEF$ có $AB = DE$ , \(\widehat B = \widehat E\) , \(\widehat A = \widehat D = 90^\circ \). Biết $AC = 9cm.$ Độ dài $DF$ là:
Cho \(\Delta ABC\) cân ở $A.$ Đường trung trực của $AC$ cắt $AB$ ở $D.$ Biết $CD$ là tia phân giác của \(\widehat {ACB}\) . Tính các góc của \(\Delta ABC\).
Cho tam giác \(ABC\) và tam giác $KHI$ có: \(\widehat A = \widehat K = 90^\circ ;\,AB = KH;\,BC = HI\) . Phát biểu nào trong các phát biểu sau là đúng:
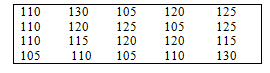
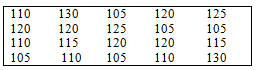
Cho bảng “tần số”

Từ bảng này hãy viết lại một bảng số liệu ban đầu.
Thu gọn đơn thức \({x^3}{y^3}.{x^2}{y^2}z\) ta được
Cho \(\left( {25{x^2}y - 10x{y^2} + {y^3}} \right) - A = 12{x^2}y - 2{y^3}.\) Đa thức \(A\) là
Đa thức \(M\) nào dưới đấy thỏa mãn \(M - \left( {3xy - 4{y^2}} \right) = {x^2} - 7xy + 8{y^2}\)
Tìm hệ số cao nhất của đa thức \(k\left( x \right)\) biết \(f\left( x \right) + k\left( x \right) = g\left( x \right)\) và \(f\left( x \right) = {x^4} - 4{x^2} + 6{x^3} + 2x - 1;\)\(g\left( x \right) = x + 3.\)
Cho \(P(x) = {x^2} - 6x + a\) . Tìm $a$ để $P\left( x \right)$ nhận $-1$ là nghiệm.
Cho hai đa thức \(f\left( x \right) = - {x^5} + 2{x^4} - {x^2} - 1;g\left( x \right) = - 6 + 2x - 3{x^3} - {x^4} + 3{x^5}\) . Giá trị của \(h\left( x \right) = f\left( x \right) - g\left( x \right)\) tại \(x = - 1\) là:
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ .\) Trên tia phân giác của góc \(A\) lấy điểm \(D\) sao cho \(AD = AB + AC.\) Khi đó tam giác \(BCD\) là tam giác gì?
Cho tam giác $ABC$ cân tại $A$ có \(\widehat B = {40^0}.\) Cho $AD$ là tia phân giác của góc \(\widehat {BAC}\). Số đo góc \(\widehat {DAB}\) là:
Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng $5cm.$ Tính cạnh $BC$ của tam giác đó biết chu vi của tam giác là $17cm.$
Cho \(\Delta ABC\) cân tại $A,$ hai đường cao $BD$ và $CE$ cắt nhau tại $I.$ Tia $AI$ cắt $BC$ tại $M.$ Khi đó \(\Delta MED\)là tam giác gì?
Cho tam giác $ABC$ vuông tại $A$ có $AB = 5cm,{\rm{ }}AC = 12cm.$ Gọi $G$ là trọng tâm tam giác $ABC{\rm{ }},$ khi đó $GA + GB + GC$ bằng: (làm tròn đến $2$ chữ số sau dấu phẩy)
Biết \((x - 1)f(x) = (x + 4)f(x + 8)\). Khi đó đa thức $f\left( x \right)$ có ít nhất là bao nhiêu nghiệm?
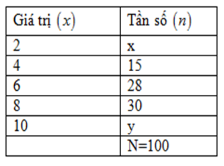
Cho bảng số liệu sau: Biết số các giá trị không nhỏ hơn $6$ là $80.$ Tìm giá trị của $x;y.\;$
Cho đa thức \(f\left( x \right) = {a_4}{x^4} + {a_3}{x^3} + {a_2}{x^2} + {a_1}x + {a_0}\) . Biết rằng \(f\left( 1 \right) = f\left( { - 1} \right)\); \(f\left( 2 \right) = f\left( { - 2} \right)\). Chọn câu đúng.
Cho \(\Delta ABC\), trên $BC$ lấy điểm $M$ bất kì nằm giữa $B$ và $C.$
So sánh \(AB + AC - BC\) và \(2.AM\)