Câu hỏi:
3 năm trước
Cho tam giác $ABC$ cân tại $A$ có \(\widehat B = {40^0}.\) Cho $AD$ là tia phân giác của góc \(\widehat {BAC}\). Số đo góc \(\widehat {DAB}\) là:
Trả lời bởi giáo viên
Đáp án đúng: d
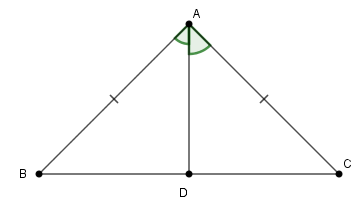
Do tam giác $ABC$ cân tại $A$ nên \(\widehat B = \widehat C = {40^0}.\)
Xét tam giác $ABC$ ta có: $\widehat A + \widehat B + \widehat C = {180^0}$$ \Leftrightarrow \widehat A = {180^0} - \widehat B - \widehat C = {180^0} - {40^0} - {40^0} = {100^0}.$
Vì $AD$ là phân giác của \(\widehat {BAC} \)\(\Rightarrow \widehat {DAB} = \widehat {DAC} = \dfrac{{\widehat A}}{2} = {50^0}\)
Hướng dẫn giải:
Áp dụng tính chất của tam giác cân và định lý tổng các góc của một tam giác.

