Cho $\Delta ABC$ cân ở $A.$ Đường trung trực của $AC$  cắt $AB$  ở $D.$ Biết $CD$  là tia phân giác của $\widehat {ACB}$ . Tính các góc của $\Delta ABC$. 

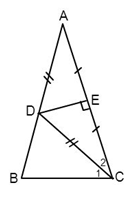
Vì đường trung trực của $AC$  cắt $AB$  tại $D$  nên suy ra $DA = DC$(tính chất đường trung trực của đoạn thẳng)

$\Rightarrow \Delta ADC$ là tam giác cân tại $D$  (dấu hiệu nhận biết tam giác cân)

$\Rightarrow \widehat A = \widehat {{C_2}}\,\left( 1 \right)$ (tính chất tam giác cân).

Vì $CD$ là đường phân giác của $\widehat {ACB} \Rightarrow \widehat {{C_1}} = \widehat {{C_2}} = \dfrac{{\widehat C}}{2}\left( 2 \right)$ (tính chất tia phân giác).

Từ (1) và (2) $\Rightarrow \widehat {ACB} = 2\widehat A$.

Lại có $\Delta ABC$ cân tại $A$  (gt) $\Rightarrow \widehat B = \widehat {ACB}$ (tính chất tam giác cân) $\Rightarrow \widehat B = 2\widehat A$

Xét $\Delta ABC$ có:

$\widehat A + \widehat B + \widehat {ACB} = {180^0} \Rightarrow \widehat A + 2\widehat A + 2\widehat A = {180^0}$

$\Rightarrow 5\widehat A = {180^0}$$\Rightarrow \widehat A = {36^0} \Rightarrow \widehat B = \widehat C = 2\widehat A = {2.36^0} = {72^0}$

Vậy $\widehat A = {36^0},\widehat B = \widehat C = {72^0}.$