Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) có \(\widehat A = 120^\circ .\) Trên tia phân giác của góc \(A\) lấy điểm \(D\) sao cho \(AD = AB + AC.\) Khi đó tam giác \(BCD\) là tam giác gì?
Trả lời bởi giáo viên
Đáp án đúng: b
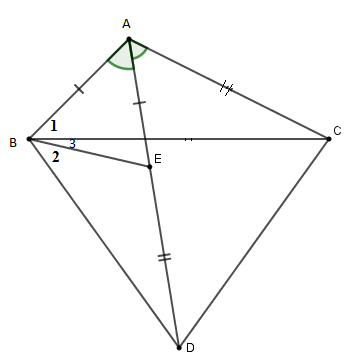
Lấy \(E \in AD\) sao cho \(AE = AB\) mà \(AD = AB + AC\) nên \(AC = DE.\)
\(\Delta ABE\) cân có \(\widehat {BAD} = 60^\circ \) nên \(\Delta ABE\) là tam giác đều suy ra \(AE = EB.\)
Thấy \(\widehat {BED} = \widehat {EBA} + \widehat {EAB} = 120^\circ \) (góc ngoài tại đỉnh \(E\) của tam giác \(ABE\) ) nên \(\widehat {BED} = \widehat {BAC}\left( { = 120^\circ } \right)\)
Suy ra \(\Delta EBD = \Delta {\rm A}BC\left( {c.g.c} \right) \Rightarrow \widehat {{B_1}} = \widehat {{B_2}}\) (hai góc tương ứng bằng nhau) và \(BD = BC\) (hai cạnh tương ứng)
Lại có $\widehat {{B_1}} + \widehat {{B_3}} = 60^\circ $ nên \(\widehat {{B_2}} + \widehat {{B_3}} = 60^\circ .\)
\(\Delta BCD\) cân tại \(B\) có \(\widehat {CBD} = 60^\circ \) nên nó là tam giác đều.
Hướng dẫn giải:
Dựa vào tính chất tổng các góc của tam giác và dựa vào tính chất tam giác cân.
