Kết quả:
0/32
Thời gian làm bài: 00:00:00
Hai phương trình tương đương là hai phương trình có
Hãy chọn câu đúng. Nếu $\Delta ABC$ và $\Delta DEF$ có $\widehat B = \widehat {D;}\,\dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}}$ thì:
Tam giác $ABC$ vuông tại $A$ có đường cao $AH$ . Cho biết $AB = 3cm$ ; $AC = 4cm$ . Tính độ dài các đoạn thẳng $HA, HB.$
Số nghiệm của phương trình \(\left| {x - 3} \right| + 3x = 7\) là
Trong các mặt của một hình hộp chữ nhật, tính số cặp mặt song song với nhau là
Phương trình \(\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) = 0\) có số nghiệm là:
Nếu 2 tam giác ABC và DEF có \(\widehat A = \widehat D\), \(\widehat C = \widehat F\) thì:
Cho hình vẽ, trong đó $DE{\rm{//}}BC$, $AD = 12,\,\,DB = 18,\,\,CE = 30$. Độ dài $AC$ bằng:
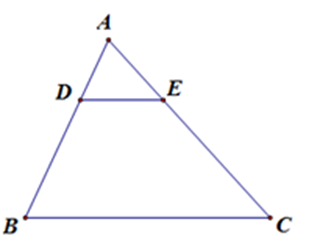
Cho \(\Delta ABC\), \(AD\) là phân giác trong của góc $A$ . Hãy chọn câu đúng:
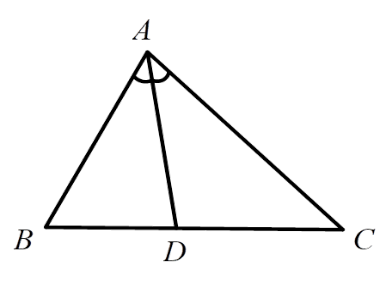
Hãy chọn câu đúng. Tính độ dài \(x,y\) của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình có cùng đơn vị đo là $cm$ .
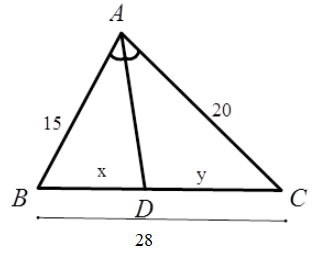
Hãy chọn câu đúng. Nếu \(a > b\) thì:
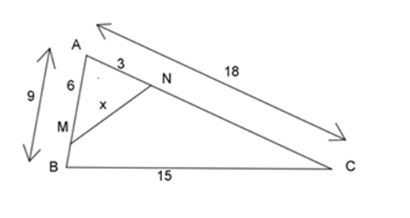
Cho hình vẽ dưới đây, tính giá trị của $x$ ?
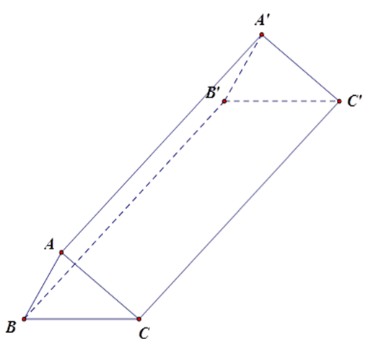
Hình lăng trụ đứng $ABC.A'B'C'$ (hình vẽ) có \(\widehat {BAC} = {90^0},AB = 6cm,AC = 8cm,{\rm{AA' = 15cm}}\) . Diện tích toàn phần của hình lăng trụ đó bằng
Cho $\Delta DHE \backsim\Delta ABC$ với tỉ số đồng dạng $\dfrac{2}{3}$. Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(I) Tỉ số hai đường cao tương ứng của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{2}{3}$.
(II) Tỉ số hai đường cao tương ứng của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$.
(III) Tỉ số diện tích của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$.
(IV) Tỉ số diện tích của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{4}{9}$.
Kết luận nào sau đây là đúng nhất khi nói về nghiệm \({x_0}\) của phương trình $\dfrac{{x + 1}}{2} + \dfrac{{x + 3}}{4} = 3 - \dfrac{{x + 2}}{3}$
Tập nghiệm của phương trình \(\left( {{x^2} + x} \right)\left( {{x^2} + x + 1} \right) = 6\) là
Cho hai biểu thức : \(A = 1 + \dfrac{1}{{2 + x}}\) và \(B = \dfrac{{12}}{{{x^3} + 8}}\) . Tìm $x$ sao cho \(A = B\) .
Một tổ sản xuất theo kế hoạch mỗi ngày phải sản xuất $50$ sản phầm. Khi thực hiện tổ đã sản xuất được $57$ sản phẩm một ngày. Do đó hoàn thành trước kế hoạch $1$ ngày và còn vượt mức $13$ sản phẩm. Hỏi theo kế hoạch tổ phải sản xuất bao nhiêu sản phẩm?
Một ô tô phải đi quãng đường $AB$ dài $60$ km trong một thời gian nhất định. Xe đi nửa đầu quãng đường với vận tốc hơn dự định $10$ km/h và đi với nửa sau kém hơn dự định $6$ km/h. Biết ô tô đến đúng dự định. Tính thời gian dự định đi quãng đường $AB$ ?
Với \(a,b,c\) bất kỳ. Hãy so sánh \(3\left( {{a^2} + {b^2} + {c^2}} \right)\) và \({\left( {a + b + c} \right)^2}\)
Bất phương trình $2{(x + 2)^2} < 2x(x + 2) + 4$ có tập nghiệm là
Cho hình vẽ, trong đó \(AB{\rm{//}}CD\) và \(DE = EC\). Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
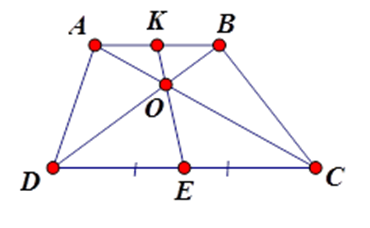
(I) \(\dfrac{{AK}}{{EC}} = \dfrac{{KB}}{{DE}}\) (II)\(AK = KB\)
(III) \(\dfrac{{AO}}{{AC}} = \dfrac{{AB}}{{DC}}\) (IV) \(\dfrac{{AK}}{{EC}} = \dfrac{{OB}}{{OD}}\)
Cho tam giác $ABC$ cân tại $A$ , đường phân giác trong của góc $B$ cắt $AC$ tại $D$ và cho biết $AB = 15$ $cm$ , $BC = 10cm$ . Khi đó $AD = $ ?
Một tam giác có cạnh nhỏ nhất bằng $8$ , hai cạnh còn lại bằng $x$ và $y$ \(\left( {x < y} \right).\) Một tam giác khác có cạnh lớn nhất bằng $27$ , hai cạnh còn lại cũng bằng $x$ và $y$ . Tính $x$ và $y$ để hai tam giác đó đồng dạng.
Cho hình bình hành $ABCD$ , điểm $F$ trên cạnh $BC$ . Tia $AF$ cắt $BD$ và $DC$ lần lượt ở $E$ và $G$ . Chọn khẳng định sai.
Cho tam giác $ABC$, phân giác $AD$ . Gọi $E,F$ lần lượt là hình chiếu của $B$ và $C$ lên $AD$ .
Chọn khẳng định đúng.
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $O$ và $O'$ lần lượt là tâm \(ABCD;\,A'B'C'D'\) . Hai mp $(ACC'A')$ và mp $\left( {BDD'B'} \right)$ cắt nhau theo đường nào?
Một hình hộp chữ nhật có đường chéo lớn bằng $17cm$ , các kích thước của đáy bằng $9cm$ và $12cm$ . Tính thể tích của hình hộp chữ nhật đó.
Tính thể tích của hình chóp tam giác đều có tất cả các cạnh đều bằng $6\,cm$ (làm tròn đến chữ số thập phân thứ hai).
Cho phương trình $\left( 1 \right):$ \(x\left( {{x^2} - 4x + 5} \right) = 0\) và phương trình \(\left( 2 \right):\) \(\left( {{x^2} - 1} \right)\left( {{x^2} + 4x + 5} \right) = 0\).
Chọn khẳng định đúng.
Một hình hộp chữ nhật có diện tích xung quanh bằng $120\,c{m^2}$ , chiều cao bằng $6cm$ . Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất.
Nghiệm của phương trình \(\left| {x + \dfrac{1}{{209}}} \right| + \left| {x + \dfrac{2}{{209}}} \right| + \left| {x + \dfrac{3}{{209}}} \right| + ... + \left| {x + \dfrac{{208}}{{209}}} \right| = 209x\) là

