Kết quả:
0/40
Thời gian làm bài: 00:00:00
Chọn câu sai:
Hãy chọn câu đúng. Điều kiện xác định của phương trình \(\dfrac{1}{{x - 2}} + 3 = \dfrac{{3 - x}}{{x - 2}}\) là
Phương trình nào sau đây không phải phương trình bậc nhất một ẩn?
Nếu tam giác $ABC$ có $MN$ // $BC$ (với \(M\in AB, N\in AC)\) thì
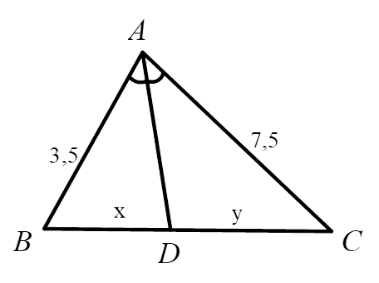
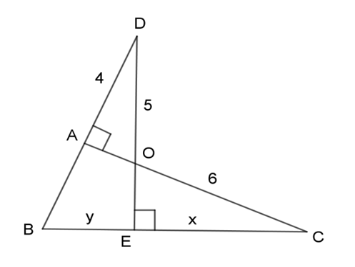
Hãy chọn câu đúng. Tỉ số \(\dfrac{x}{y}\) của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình cùng đơn vị đo là $cm$ .
Cho $\Delta DHE \backsim\Delta ABC$ với tỉ số đồng dạng $\dfrac{2}{3}$. Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(I) Tỉ số hai đường cao tương ứng của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{2}{3}$.
(II) Tỉ số hai đường cao tương ứng của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$.
(III) Tỉ số diện tích của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$.
(IV) Tỉ số diện tích của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{4}{9}$.
Cho tam giác ABC có \(AB = 12cm,\;AC = 18cm,\;BC = 27cm.\) Điểm $D$ thuộc cạnh $BC$ sao cho
$CD = 12\,cm$ . Tính độ dài $AD$ .
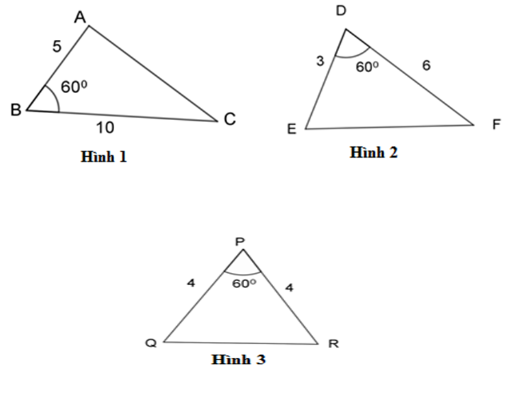
Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:
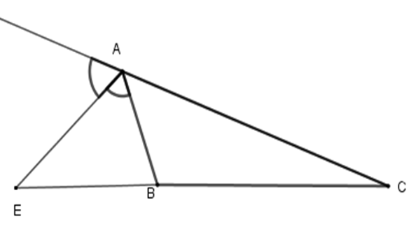
Hãy chọn câu sai. Cho hình vẽ với $AB<AC$:
Cho \(\Delta ABC\)\(\backsim\)\(\Delta IKH\). Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(I) \(\dfrac{{HI}}{{AC}} = \dfrac{{KH}}{{BC}} = \dfrac{{KI}}{{AB}};\)
(II) \(\dfrac{{AB}}{{IK}} = \dfrac{{AC}}{{HI}} = \dfrac{{BC}}{{KH}};\)
(III) \(\dfrac{{AC}}{{IH}} = \dfrac{{AB}}{{KI}} = \dfrac{{BC}}{{IK}}.\)
Cho \(\Delta ABC\), đường phân giác góc $B$ cắt $AC$ tại $D$ và cho biết $AB = 10{\rm{ }}cm,{\rm{ }}BC = 15{\rm{ }}cm,{\rm{ }}AD = 6{\rm{ }}cm.$ Tính $AC = $ ?
Chỉ ra câu sai?
Cho tam giác $ABC$ cân tại $A$, đường cao $CE$. Tính $AB$, biết $BC = 24$cm và $BE = 9$cm.
Cho tứ giác \(ABCD\), lấy bất kỳ \(E \in BD\) . Qua \(E\) vẽ \(EF\) song song với \(AD\)( \(F\) thuộc \(AB\)), vẽ \(EG\) song song với \(DC\)(\(G\) thuộc\(BC\)). Chọn khẳng định sai.
Cho \(\Delta ABC\) đồng dạng với \(\Delta MNP\). Biết \(AB = 5cm,BC = 6cm,MN = 10cm,MP = 5cm\). Hãy chọn câu đúng:
Chu vi một mảnh vườn hình chữ nhật là \(45\,m\) . Biết chiều dài hơn chiều rộng \(5\,m\) . Nếu gọi chiều rộng mảnh vườn là \(x\) \(\left( {x > 0;\,{\rm{m}}} \right)\) thì Phương trình của bài toán là
Hãy chọn câu trả lời đúng. Nếu tam giác $ABC$ đồng dạng với tam giác \(A'B'C'\) theo tỉ số $k$ thì tỉ số chu vi của hai tam giác đó bằng
Hai phương trình tương đương là hai phương trình có
Cho biết \(2x - 2 = 0\) . Tính giá trị của \(5{x^2} - 2\) .
Phương trình \(\dfrac{{3x - 5}}{{x - 1}} - \dfrac{{2x - 5}}{{x - 2}} = 1\) có số nghiệm là
Cho \(\Delta ABC\), \(AE\) là phân giác ngoài của góc A. Hãy chọn câu đúng:
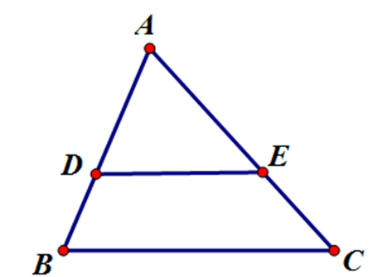
Cho hình thang $ABCD$ (\(AB\,{\rm{//}}\,CD\)) có \(\widehat {ADB} = \widehat {BCD}\), $AB = 2cm$ , \(BD = \sqrt 5 \,cm\), ta có:
Xe thứ hai đi chậm hơn xe thứ nhất là $15$ km/h. Nếu gọi vận tốc xe thứ hai là \(x\) (km/h) thì vận tốc xe thứ nhất là:
Số \({x_0}\) được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\) khi
Gọi \({x_1}\) là nghiệm của phương trình ${x^3} + 2{\left( {x - 1} \right)^2} - 2\left( {x - 1} \right)\left( {x + 1} \right) = {x^3} + x - 4 - \left( {x - 4} \right)$ và \({x_2}\) là nghiệm của phương trình $x + \dfrac{{2x - 7}}{2} = 5 - \dfrac{{x + 6}}{2} + \dfrac{{3x + 1}}{5}$. Tính \({x_1}.{x_2}\)
Tìm m để phương trình \(\left( {2m - 5} \right)x - 2{m^2} + 8 = 43\) có nghiệm \(x = - 7\).
Số nghiệm của phương trình $\dfrac{{{x^2} + 3x + 2}}{{x + 3}} - \dfrac{{{x^2} + 2x + 1}}{{x - 1}} = \dfrac{{4x + 4}}{{{x^2} + 2x - 3}}$ là
Một đội máy cày dự định cày $40$ ha ruộng $1$ ngày. Do sự cố gắng, đội đã cày được $52$ ha mỗi ngày. Vì vậy, chẳng những đội đã hoàn thành sớm hơn $2$ ngày mà còn cày vượt mức được $4$ ha nữa. Tính diện tích ruộng đội phải cày theo dự định.
Một hình chữ nhật có chu vi $372m$ nếu tăng chiều dài $21m$ và tăng chiều rộng $10m$ thì diện tích tăng $2862\,{m^2}.$ Chiều dài của hình chữ nhật là:
Cho tam giác $ABC$ cân tại $A$ , đường phân giác trong của góc $B$ cắt $AC$ tại $D$ và cho biết $AB = 15$ $cm$ , $BC = 10cm$ . Khi đó $AD = $ ?
Cho tam giác $ABC$ , điểm $M$ thuộc cạnh $BC$ sao cho \(\dfrac{{MB}}{{MC}} = \dfrac{1}{2}.\) Đường thẳng đi qua M và song song với $AC$ cắt $AB$ ở $D$ . Đường thẳng đi qua $M$ và song song với $AB$ cắt $AC$ ở $E$ . Biết chu vi tam giác $ABC$ bằng \(30\,cm\) . Chu vi của các tam giác $DBM$ và $EMC$ lần lượt là
Tứ giác $ABCD$ có $AB = 8\,cm,BC = 15\,cm,CD = 18\,cm,AD = 10\,cm,BD = 12\,cm.$
Chọn câu đúng nhất:
Cho tam giác nhọn ABC có \(\widehat C = {40^0}\). Vẽ hình bình hành $ABCD$ . Gọi $AH,AK$ theo thứ tự là các đường cao của các tam giác $ABC,ACD$ . Tính số đo $\widehat {AKH}$ .
Tam giác ABC có $\widehat A = 2\widehat B$, $AB = 11\,{\rm{cm}}$, $AC = 25\,{\rm{cm}}$. Tính độ dài cạnh $BC$ .
Với giả thiết được cho trong hình, kết quả nào sau đây là đúng ?
Cho đoạn $AC$ vuông góc với $CE.$ Nối $A$ với trung điểm $D$ của $CE$ và $E$ với trung điểm $B$ của $AC,{\rm{ }}AD$ và $EB$ cắt nhau tại $F.$ Cho $BC = CD = 15{\rm{ }}cm.$ Tính diện tích tam giác $DEF$ theo đơn vị $c{m^2}$ ?
Cho tam giác ABC có AM là đường trung tuyến, N là điểm trên đoạn thẳng AM. Gọi D là giao điểm của CN và AB, E là giao điểm của BN và AC. Chọn khẳng định đúng nhất.
Cho phương trình: \(\left( {4{m^2} - 9} \right)x = 2{m^2} + m - 3\) . Tìm m để phương trình có vô số nghiệm
Biết rằng phương trình \({\left( {{x^2} - 1} \right)^2} = 4x + 1\) có nghiệm lớn nhất là \({x_0}\) . Chọn hẳng định đúng.
Cho hình chữ nhật $ABCD$ có $E$ là trung điểm của $AB.$ Tia $DE$ cắt $AC$ ở $F,$ cắt $CB$ ở $G.$ Chọn câu đúng.

