Kết quả:
0/40
Thời gian làm bài: 00:00:00
Phương trình bậc nhất một ẩn có dạng
Phương trình \(\dfrac{{6x}}{{9 - {x^2}}} = \dfrac{x}{{x + 3}} - \dfrac{3}{{3 - x}}\) có nghiệm là
Số thứ nhất gấp $6$ lần số thứ hai. Nếu gọi số thứ nhất là $x$ thì số thứ hai là:
Cho 2 tam giác RSK và PQM có \(\dfrac{{RS}}{{PQ}} = \dfrac{{RK}}{{PM}} = \dfrac{{SK}}{{QM}}\), khi đó ta có:
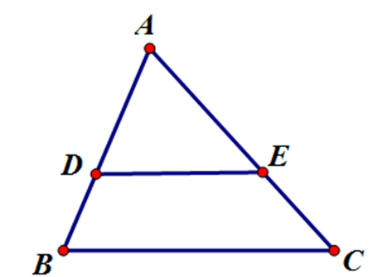
Hãy chọn câu sai. Cho hình vẽ với $AB<AC$:
Phương trình \(2x - 3 = 12 - 3x\) có bao nhiêu nghiệm?
Cho $\Delta DHE \backsim\Delta ABC$ với tỉ số đồng dạng $\dfrac{2}{3}$. Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(I) Tỉ số hai đường cao tương ứng của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{2}{3}$.
(II) Tỉ số hai đường cao tương ứng của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$.
(III) Tỉ số diện tích của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$.
(IV) Tỉ số diện tích của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{4}{9}$.
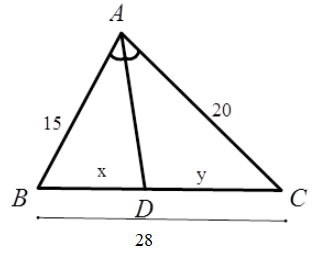
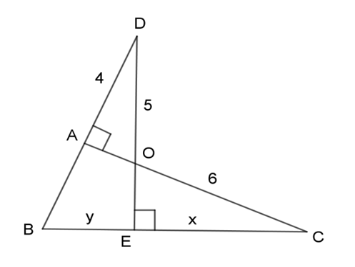
Hãy chọn câu đúng. Tính độ dài \(x,y\) của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình có cùng đơn vị đo là $cm$ .
Chu vi một mảnh vườn hình chữ nhật là \(45\,m\) . Biết chiều dài hơn chiều rộng \(5\,m\) . Nếu gọi chiều rộng mảnh vườn là \(x\) \(\left( {x > 0;\,{\rm{m}}} \right)\) thì Phương trình của bài toán là
Hãy chọn câu đúng. Điều kiện xác định của phương trình \(\dfrac{1}{{x - 2}} + 3 = \dfrac{{3 - x}}{{x - 2}}\) là
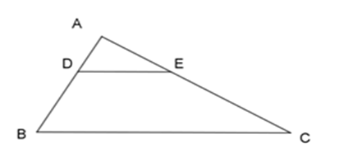
Cho hình vẽ biết \(DE//BC\). Khẳng định nào sau đây là đúng?
Cho tam giác $ABC$ cân tại $A$, đường cao $CE$. Tính $AB$, biết $BC = 24$cm và $BE = 9$cm.
Chọn câu sai:
Hai phương trình tương đương là hai phương trình có
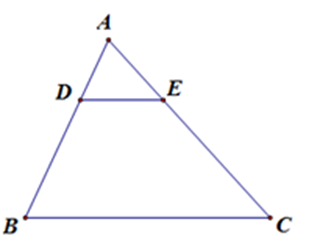
Cho hình vẽ, trong đó $DE{\rm{//}}BC$, $AD = 12,\,\,DB = 18,\,\,CE = 30$. Độ dài $AC$ bằng:
Cho 2 tam giác $MNP$ và $QRS$ đồng dạng với nhau theo tỉ số $k.$ Tỷ số diện tích của 2 tam giác $MNP$ và $QRS$ là:
Cho hình thang $ABCD$ (\(AB\,{\rm{//}}\,CD\)) có \(\widehat {ADB} = \widehat {BCD}\), $AB = 2cm$ , \(BD = \sqrt 5 \,cm\), ta có:
Cho biết \(\dfrac{{AB}}{{CD}} = \dfrac{5}{7}\) và đoạn thẳng $AB$ ngắn hơn đoạn thẳng $CD$ là $10{\rm{ }}cm.$ Tính độ dài các đoạn thẳng$AB,{\rm{ }}CD$ ?
Phương trình \(\dfrac{x}{{x - 5}} - \dfrac{3}{{x - 2}} = 1\) có nghiệm là
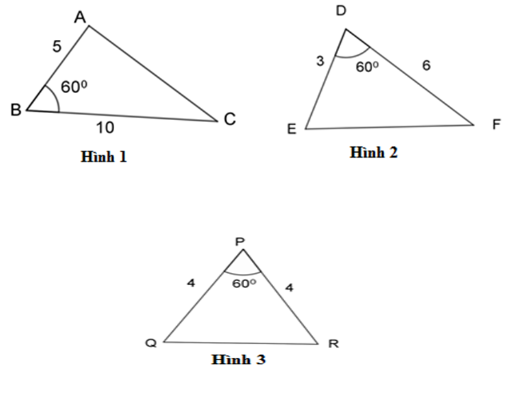
Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:
Phương trình nào sau đây vô nghiệm?
Cho tam giác ABC có \(AB = 12cm,\;AC = 18cm,\;BC = 27cm.\) Điểm $D$ thuộc cạnh $BC$ sao cho
$CD = 12\,cm$ . Tính độ dài $AD$ .
Hãy chọn câu sai.
Nếu 2 tam giác ABC và DEF có \(\widehat A = \widehat D\), \(\widehat C = \widehat F\) thì:
Tính tổng các nghiệm của phương trình \(\left| {3x + 6} \right| - 2 = 4\), biết phương trình có hai nghiệm phân biệt.
Tổng các nghiệm của phương trình \(\left( {{x^2} - 4} \right)\left( {x + 6} \right)\left( {x - 8} \right) = 0\) là:
Tìm số tự nhiên có bốn chữ số, biết rằng nếu viết thêm chữ số $1$ vào đằng trước ta được số $A$ có năm chữ số, nếu viết them chữ số $4$ vào đằng sau ta được số $B$ có năm chữ số, trong đó $B$ gấp bốn lần $A$ .
Điều kiện xác định của phương trình \(1 + \dfrac{x}{{3 - x}} = \dfrac{{5x}}{{\left( {x + 2} \right)\left( {3 - x} \right)}} + \dfrac{2}{{x + 2}}\) là:
Cho hình vẽ, trong đó \(AB{\rm{//}}CD\) và \(DE = EC\). Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
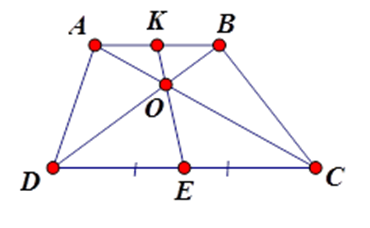
(I) \(\dfrac{{AK}}{{EC}} = \dfrac{{KB}}{{DE}}\) (II)\(AK = KB\)
(III) \(\dfrac{{AO}}{{AC}} = \dfrac{{AB}}{{DC}}\) (IV) \(\dfrac{{AK}}{{EC}} = \dfrac{{OB}}{{OD}}\)
Cho tam giác $ABC$ cân tại $A$ , đường phân giác trong của góc $B$ cắt $AC$ tại $D$ và cho biết $AB = 15$ $cm$ , $BC = 10cm$ . Khi đó $AD = $ ?
Cho hình bình hành $ABCD$ . Trên đường chéo $AC$ lấy điểm $E$ sao cho $AC = 3AE$ . Qua $E$ vẽ đường thẳng song song với $CD$ , cắt $AD$ và $BC$ theo thứ tự ở $M$ và $N$ . Cho các khẳng định sau:
(I) \(\Delta AME\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng \( k{ _1} = \dfrac{1}{3}.\)
(II) \(\Delta CBA\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng bằng \({k_2} = 1\) .
(III) \(\Delta CNE\)\(\backsim\)\(\Delta ADC,\) tỉ số đồng dạng \({k_3} = \dfrac{2}{3}.\)
Chọn câu đúng.
\(\Delta ABC\)\(\backsim\)$\Delta DEF$ theo tỉ số \({k_1},\) \(\Delta MNP\)\(\backsim\)$\Delta DEF$ theo tỉ số \({k_2}.\) \(\Delta ABC\)\(\backsim\)$\Delta MNP$ theo tỉ số nào?
Cho tam giác $ABC$ có $AB = 9\,cm,AC = 16\,cm,BC = 20\,cm$ . Khi đó
Tam giác ABC có $\widehat A = 2\widehat B$, $AB = 11\,{\rm{cm}}$, $AC = 25\,{\rm{cm}}$. Tính độ dài cạnh $BC$ .
Với giả thiết được cho trong hình, kết quả nào sau đây là đúng ?
Tỉ số các cạnh bé nhất của 2 tam giác đồng dạng bằng \(\dfrac{2}{5}\). Tính chu vi p, \(p'\) của 2 tam giác đó, biết \(p' - p = 18\)?
Giải phương trình: \(20{\left( {\dfrac{{x - 2}}{{x + 1}}} \right)^2} - 5{\left( {\dfrac{{x + 2}}{{x - 1}}} \right)^2} + 48\dfrac{{{x^2} - 4}}{{{x^2} - 1}} = 0\) ta được các nghiệm là \({x_1};{x_2}\) với \({x_1} < {x_2}\) . Tính \(3{x_1} - {x_2}.\)
Nghiệm của phương trình \(\dfrac{{x + a}}{{b + c}} + \dfrac{{x + b}}{{a + c}} + \dfrac{{x + c}}{{a + b}} = - 3\) là
Cho \(\Delta ABC\) vuông tại $A,$ đường cao $AH.$ Gọi $I$ và $K$ lần lượt là hình chiếu của $H$ lên $AB$ và $AC.$ Tam giác \(AIK\) đồng dạng với tam giác nào dưới đây?
Cho phương trình $\left( 1 \right):$ \(x\left( {{x^2} - 4x + 5} \right) = 0\) và phương trình \(\left( 2 \right):\) \(\left( {{x^2} - 1} \right)\left( {{x^2} + 4x + 5} \right) = 0\).
Chọn khẳng định đúng.

