Kết quả:
0/10
Thời gian làm bài: 00:00:00
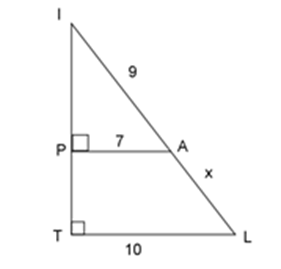
Tính giá trị của $x$ trong hình dưới đây:
Cho tam giác ABC có \(AB = 12cm,\;AC = 18cm,\;BC = 27cm.\) Điểm $D$ thuộc cạnh $BC$ sao cho
$CD = 12\,cm$ . Tính độ dài $AD$ .
Hãy chọn câu đúng. Nếu $\Delta ABC$ và $\Delta DEF$ có $\widehat B = \widehat {D;}\,\dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}}$ thì:
Nếu 2 tam giác ABC và DEF có \(\widehat A = \widehat D\), \(\widehat C = \widehat F\) thì:
Cho \(\Delta ABC\), lấy 2 điểm $D$ và $E$ lần lượt nằm bên cạnh $AB$ và $AC$ sao cho \(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\). Kết luận nào sai?
Cho tam giác $ABC$ . Các điểm $D,E,F$ theo thứ tự là trung điểm của $BC,CA,AB$ . Các điểm $A',B',C'$ theo thứ tự là trung điểm của $EF,DF,DE$ . Chọn câu đúng?
Cho tam giác $ABC$ có $AB = 9\,cm,AC = 16\,cm,BC = 20\,cm$ . Khi đó
Cho tam giác nhọn ABC có \(\widehat C = {40^0}\). Vẽ hình bình hành $ABCD$ . Gọi $AH,AK$ theo thứ tự là các đường cao của các tam giác $ABC,ACD$ . Tính số đo $\widehat {AKH}$ .
Cho hình bình hành $ABCD$ , điểm $F$ trên cạnh $BC$ . Tia $AF$ cắt $BD$ và $DC$ lần lượt ở $E$ và $G$ . Chọn khẳng định sai.
Tam giác ABC có $\widehat A = 2\widehat B$, $AB = 11\,{\rm{cm}}$, $AC = 25\,{\rm{cm}}$. Tính độ dài cạnh $BC$ .

