Câu hỏi:
2 năm trước
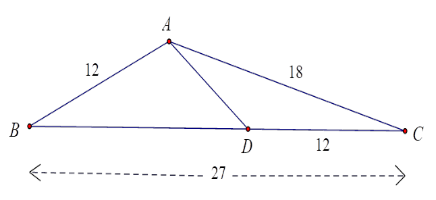
Cho tam giác ABC có \(AB = 12cm,\;AC = 18cm,\;BC = 27cm.\) Điểm $D$ thuộc cạnh $BC$ sao cho
$CD = 12\,cm$ . Tính độ dài $AD$ .
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có
\(\begin{array}{l}\dfrac{{AC}}{{DC}} = \dfrac{{18}}{{12}} = \dfrac{3}{2};\,\dfrac{{CB}}{{CA}} = \dfrac{{27}}{{18}} = \dfrac{3}{2}\\ \Rightarrow \dfrac{{CA}}{{CD}} = \dfrac{{CB}}{{CA}}\end{array}\)
Xét \(\Delta ACB\) và \(\Delta DCA\) có \(\widehat C\) chung và \(\dfrac{{CA}}{{CD}} = \dfrac{{CB}}{{CA}}\,\left( {cmt} \right)\)
Nên $\Delta ACB$ \(\backsim\) $\Delta DCA$ (c.g.c)
\(\begin{array}{l} \Rightarrow \dfrac{{AC}}{{DC}} = \dfrac{{AB}}{{DA}} \Leftrightarrow \dfrac{3}{2} = \dfrac{{12}}{{DA}}\\ \Rightarrow DA = \dfrac{{2.12}}{3} = 8\,cm\end{array}\)
Hướng dẫn giải:
Bước 1: Lập tỉ lệ cạnh để chứng minh \(\Delta ACB\) và \(\Delta DCA\) đồng dạng (cạnh-góc-cạnh)
Bước 2: Từ đó suy ra tỉ lệ cạnh còn lại để tính $AD$ .
