Đề kiểm tra 1 tiết chương 7: Tam giác đồng dạng - Đề số 1

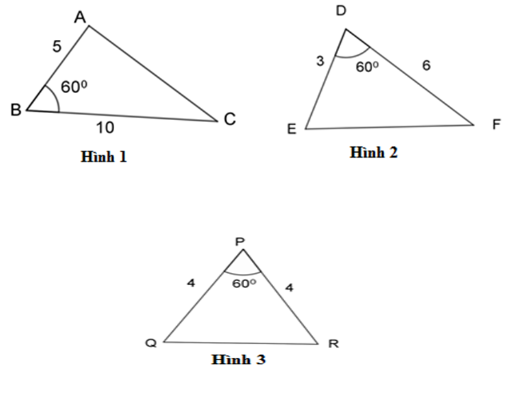
Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:

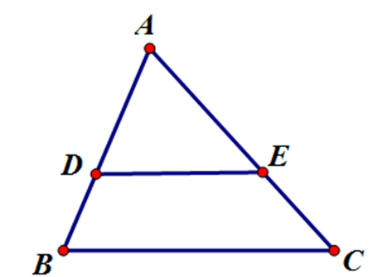
Cho $\Delta ABC$, lấy 2 điểm $D$ và $E$ lần lượt nằm bên cạnh $AB$ và $AC$ sao cho $\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}$. Kết luận nào sai?

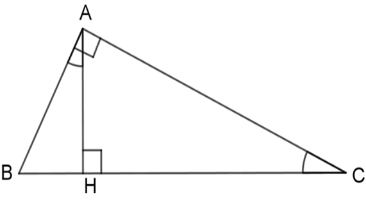
Cho  hình vẽ dưới đây với $\widehat {BAH} = \widehat {ACH}$ .

Khi đó các mệnh đề

(I) $\Delta AHB\backsim\Delta CHA\;(g - g)$

(II) $\Delta AHC\backsim\Delta BAC\;(g - g)$

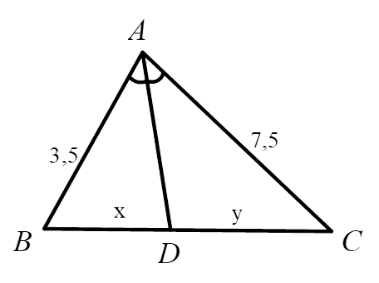
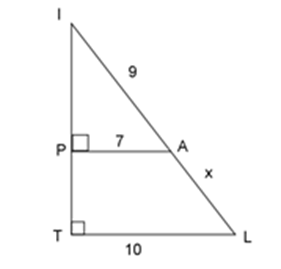
Hãy chọn câu đúng. Tỉ số $\dfrac{x}{y}$ của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình cùng đơn vị đo là $cm$ .

Cho tam giác $ABC$ cân tại $A$, đường cao $CE$. Tính $AB$, biết $BC = 24$cm và $BE = 9$cm.

Tam giác $ABC$  vuông tại $A$ có đường cao $AH$ . Cho biết $AB = 3cm$ ; $AC = 4cm$ . Tính độ dài các đoạn thẳng  $HA, HB.$

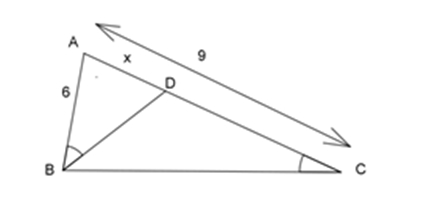
Cho hình bên biết $AB = 6\,cm,AC = 9\,cm$ , $\widehat {ABD} = \widehat {BCA}$.

Độ dài đoạn $AD$  là:

Hãy chọn câu sai. Cho hình vẽ với $AB<AC$: 

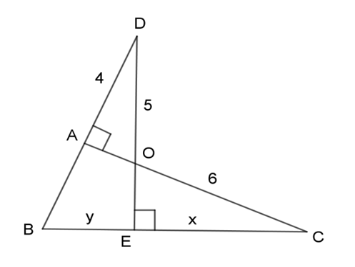
Tính giá trị của $x$  trong hình dưới đây:

Cho  tứ giác $ABCD$, lấy bất kỳ $E \in BD$ . Qua $E$ vẽ $EF$ song song với $AD$( $F$ thuộc $AB$), vẽ $EG$ song song với $DC$($G$ thuộc$BC$). Chọn khẳng định sai.

Cho tam giác $ABC$ có $AB = 9\,cm$, điểm $D$ thuộc cạnh $AB$ sao cho $AD = 6\,cm$. Kẻ $DE$ song song  với $BC$ $\left( {E \in AC} \right)$, kẻ $EF$ song song với $CD$ $\left( {F \in AB} \right)$. Tính độ dài $AF$ .

Cho tam giác $ABC,AB = AC = 10cm,$$BC = 12cm.$ Gọi $I$ là giao điểm của các đường phân giác của tam giác $ABC.$ Tính $BI$ ?

Cho tam giác $ABC$  cân tại $A$ , đường phân giác trong của  góc $B$ cắt $AC$ tại $D$ và cho biết $AB = 15$ $cm$ , $BC = 10cm$ . Khi đó $AD =$ ?

Cho tam giác $ABC$ . Các điểm $D,E,F$ theo thứ tự là trung điểm của $BC,CA,AB$ . Các điểm $A',B',C'$ theo thứ tự là trung điểm của $EF,DF,DE$ . Chọn câu đúng?

Tứ giác $ABCD$ có $AB = 8\,cm,BC = 15\,cm,CD = 18\,cm,AD = 10\,cm,BD = 12\,cm.$

Chọn câu đúng nhất:

Cho tam giác $ABC$  có $AB = 9\,cm,AC = 16\,cm,BC = 20\,cm$ . Khi đó

Cho tam giác nhọn ABC có $\widehat C = {40^0}$. Vẽ hình bình hành $ABCD$ . Gọi $AH,AK$ theo thứ tự là các đường cao của các tam giác $ABC,ACD$ . Tính số đo $\widehat {AKH}$ .

Tam giác ABC có $\widehat A = 2\widehat B$, $AB = 11\,{\rm{cm}}$, $AC = 25\,{\rm{cm}}$. Tính độ dài cạnh $BC$ .

Cho tam giác $ABC$, phân giác $AD$ . Gọi $E,F$ lần lượt là hình chiếu của $B$  và $C$  lên $AD$ .

Chọn khẳng định đúng.

Với giả thiết được cho trong hình, kết quả nào sau đây là đúng ?