Câu hỏi:
2 năm trước
Cho hình vẽ dưới đây với \(\widehat {BAH} = \widehat {ACH}\) .
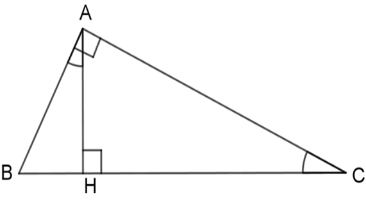
Khi đó các mệnh đề
(I) \(\Delta AHB\backsim\Delta CHA\;(g - g)\)
(II) \(\Delta AHC\backsim\Delta BAC\;(g - g)\)
Trả lời bởi giáo viên
Đáp án đúng: d
Xét $2$ tam giác vuông $AHB$ và $CHA$ có: \(\widehat {BAH} = \widehat {ACH}\) (gt)
\( \Rightarrow \Delta AHB\backsim\Delta CHA\;(g - g)\)
\( \Rightarrow \) (I) đúng.
Xét $2$ tam giác vuông $AHC$ và $BAC$ có:
\(\widehat C\) chung
\( \Rightarrow \Delta AHC\backsim\Delta BAC\;(g - g)\)
\( \Rightarrow \) (II) đúng.
Vậy cả (I) và (II) đều đúng.
Hướng dẫn giải:
- Áp dụng lý thuyết về các trường hợp đồng dạng của tam giác vuông để chứng minh các cặp tam giác vuông đồng dạng với nhau, từ đó chọn đáp án đúng.
Giải thích thêm:
- Học sinh cần viết tỉ lệ đồng dạng theo đúng thứ tự đỉnh, cạnh tương ứng của 2 tam giác.
