Trả lời bởi giáo viên
Đáp án đúng: c
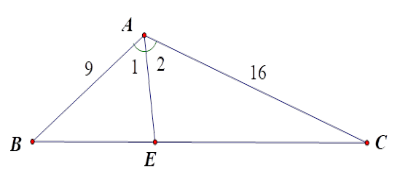
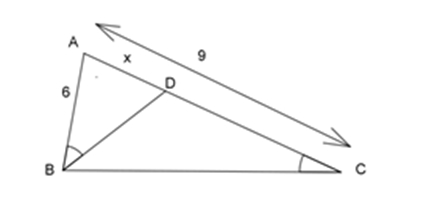
Kẻ đường phân giác $AE$ của \(\widehat {BAC}\) . Theo tính chất đường phân giác, ta có:
$\dfrac{{BE}}{{EC}} = \dfrac{{AB}}{{AC}} = \dfrac{9}{{16}}$ nên
$\dfrac{{BE + EC}}{{EC}} = \dfrac{{9 + 16}}{{16}}$ hay $\dfrac{{20}}{{EC}} = \dfrac{{25}}{{16}}.$
Suy ra $EC = 12,8\,cm$ .
Xét \(\Delta ACB\) và \(\Delta ECA\) có
\(\widehat C\) là góc chung;
$\dfrac{{AC}}{{CB}} = \dfrac{{EC}}{{CA}}$ (vì $\dfrac{{16}}{{20}} = \dfrac{{12,8}}{{16}}$).
Do đó \(\Delta ACB \backsim \Delta ECA\) (c.g.c) suy ra \(\widehat B = {\widehat A_2}\), tức là \(\widehat B = \widehat {\dfrac{A}{2}}\).
Hướng dẫn giải:
+ Kẻ đường phân giác $AE$ của \(\widehat {BAC}\) sau đó sử dụng tính chất đường phân giác của tam giác để tính \(EC\) .
+ Chứng minh \(\Delta ACB \backsim \Delta ECA\) (c-g-c) suy ra mối quan hệ giữa các góc.
