Câu hỏi:
2 năm trước
Cho tam giác $ABC$ cân tại $A$ , đường phân giác trong của góc $B$ cắt $AC$ tại $D$ và cho biết $AB = 15$ $cm$ , $BC = 10cm$ . Khi đó $AD = $ ?
Trả lời bởi giáo viên
Đáp án đúng: c
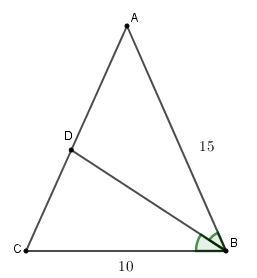
Vì $BD$ là đường phân giác của \(\widehat {ABC}\) nên:
\(\dfrac{{AD}}{{DC}} = \dfrac{{AB}}{{BC}}\)
Suy ra: \(\dfrac{{AD}}{{DC + AD}} = \dfrac{{AB}}{{BC + AB}}\)
(theo tính chất dãy tỉ số bằng nhau)
\( \Rightarrow \dfrac{{AD}}{{AC}} = \dfrac{{AB}}{{BC + AB}}\)
Mà tam giác $ABC$ cân tại $A$ nên $AC = AB = 15cm.$\( \Rightarrow \dfrac{{AD}}{{15}} = \dfrac{{15}}{{15 + 10}} \)\(\Rightarrow AD = \dfrac{{15.15}}{{25}} = 9\;cm\)
Hướng dẫn giải:
Kết hợp tính chất định lý, đã học và tính chất đường phân giác của tam giác để tìm ra tỉ lệ thức phù hợp, từ đó tìm ra độ dài $AD$ .
Giải thích thêm:
Một số em vận dụng tỉ lệ thức sai dẫn đến sai kết quả.
Câu hỏi khác
- Đề kiểm tra giữa học kì 2 - đề số 1 Toán 8 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 1 Toán 8 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 2 Toán 8 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 4 Toán 8 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 3 Toán 8 có lời giải chi tiết
