Câu hỏi:
2 năm trước
Cho tam giác ABC, phân giác AD . Gọi E,F lần lượt là hình chiếu của B và C lên AD .
Chọn khẳng định đúng.
Trả lời bởi giáo viên
Đáp án đúng: c
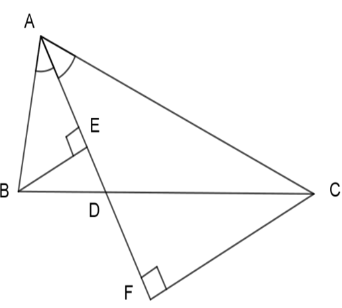
Xét 2 tam giác vuông ABE và ACF ta có:
^BAE=^CAF (vì AD là tia phân giác của góc A)
⇒ΔABE∽
\Rightarrow \dfrac{{AE}}{{AF}} = \dfrac{{BE}}{{CF}}\;(1)
Xét 2 tam giác vuông BDE và CDF ta có:
\widehat {EDB} = \widehat {FDC} (2 góc đối đỉnh)
\Rightarrow \Delta BDE\backsim\Delta CDF(g – g)
\Rightarrow \dfrac{{BE}}{{CF}} = \dfrac{{DE}}{{DF}}\;(2)
Từ (1) và (2) ta có:
\dfrac{{AE}}{{AF}} = \dfrac{{DE}}{{DF}} \Leftrightarrow AE.DF = AF.DE (đpcm)
Hướng dẫn giải:
- Chứng minh các cặp tam giác đồng dạng phù hợp để tìm ra tỉ lệ thức thích hợp.
- Từ đó rút ra điều cần chứng minh.
Giải thích thêm:
- Học sinh cần viết tỉ lệ đồng dạng theo đúng thứ tự đỉnh, cạnh tương ứng của 2 tam giác.
- Học sinh cần chú ý trong kĩ năng đại số tránh mắc sai lầm trong tính toán.
