Tính thể tích của hình chóp tam giác đều có tất cả các cạnh đều bằng $6\,cm$ (làm tròn đến chữ số thập phân thứ hai).
Trả lời bởi giáo viên
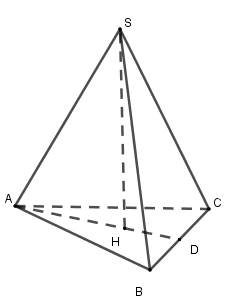
Chóp tam giác đều \(S.ABC\) có \(SH \bot \left( {ABC} \right)\) nên \(H\) là trọng tâm tam giác \(ABC\) và \(D\) là trung điểm \(BC\) .
Áp dụng định lý Pytago cho tam giác \(ABD\) vuông tại $D$ ta có
\(AD = \sqrt {A{B^2} - B{D^2}} \)\( = \sqrt {{6^2} - {3^2}} = 3\sqrt 3 \) nên diện tích đáy \(S = \dfrac{1}{2}AD.BC \)\( = \dfrac{1}{2}.3\sqrt 3 .6 = 9\sqrt 3 \,c{m^2}\) .
Vì \(H\) là trọng tâm tam giác \(ABC \Rightarrow AH = \dfrac{2}{3}AD = \dfrac{2}{3}.3\sqrt 3 = 2\sqrt 3 \) .
Áp dụng định lý Pytago cho tam giác \(ASH\) vuông tại \(H\) ta được \(SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{6^2} - {{\left( {2\sqrt 3 } \right)}^2}} = 2\sqrt 6 \)
Từ đó thể tích hình chóp là \(V = \dfrac{1}{3}SH.{S_{ABC}} = \dfrac{1}{3}.2\sqrt 6 .9\sqrt 3 \approx 25,46\,c{m^3}\) .

