Giải Toán 11 Bài 5: Xác suất của biến cố

70 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Toán 11 Bài 5: Xác suất của biến cố chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Xác suất của biến cố lớp 11.

Giải bài tập Toán 11 Bài 5: Xác suất của biến cố

Trả lời câu hỏi giữa bài

Trả lời hoạt động 1 trang 66 sgk Đại số và Giải tích 11: Từ một hộp chứa bốn quả cầu ghi chứ a, hai quả cầu ghi chữ b và hai quả cầu ghi chữ c (h.34), lấy ngẫu nhiên một quả. Kí hiệu:

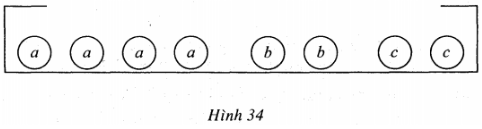
A: “Lấy được quả ghi chữ a”;

B: “Lấy được quả ghi chữ b”;

C: “Lấy được quả ghi chữ c”.

Có nhận xét gì về khả năng xảy ra của các biến cố A, B và C? Hãy so sánh chúng với nhau.

Lời giải:

Khả năng xảy ra của biến cố A là: $\frac{4}{8}$ = 0,5

Khả năng xảy ra của biến cố B là: $\frac{2}{8}$ = 0,25

Khả năng xảy ra của biến cố C là: $\frac{2}{8}$ = 0,25

⇒ Khả năng xảy ra của biến cố A lớn hơn khả năng xảy ra của biến cố B

Và khả năng xảy ra của biến cố B bằng khả năng xảy ra của biến cố C

Trả lời hoạt động 2 trang 69 sgk Đại số và Giải tích 11: Chứng minh các tính chất a), b) và c).

a. P(∅) = 0, P(Ω) = 1.

b. 0 ≤ P(A) ≤ 1, với mọi biến cố A.

c. Nếu A và B xung khắc, thì

P(A ∪ B) = P(A) + P(B) (công thức cộng xác suất).

Lời giải:

a. Theo định nghĩa xác suất của biến cố ta có:

$\begin{aligned} P (\emptyset) = \frac{n (\emptyset)}{n (Ω)} = \frac{0}{n (Ω)} = 0 \\ P (Ω) = \frac{n (Ω)}{n (Ω)} = 1 \end{aligned}$

$\begin{aligned} n (\emptyset) \leq n (A) \leq n (Ω) \Rightarrow \frac{n (\emptyset)}{n (Ω)} \leq \frac{n (A)}{n (Ω)} \leq \frac{n (Ω)}{n (Ω)} \\ \Rightarrow P (\emptyset) \leq P (A) \leq P (Ω) \end{aligned}$

hay $0 \leq P (A) \leq 1$ (từ chứng minh câu a)

c. Nếu A và B xung khắc, ta có:

$\begin{aligned} n (A \cup B) = n (A) + n (B) \\ \Rightarrow \frac{n (A \cup B)}{n (Ω)} = \frac{n (A)}{n (Ω)} + \frac{n (B)}{n (Ω)} \\ \Rightarrow P (A \cup B) = P (A) + P (B) \end{aligned}$

Bài tập (trang 74, 75 sgk Đại số và Giải tích 11)

Bài 1 trang 74 sgk Đại số và Giải tích 11: Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất hai lần.

a. Hãy mô tả không gian mẫu.

b. Xác định các biến cố sau:

A: "Tổng số chấm xuất hiện trong hai lần gieo không bé hơn $10$ ";

B: "Mặt $5$ chấm xuất hiện ít nhất một lần".

c. Tính

P (A), P (B)

Phương pháp giải:

Khi gieo: mỗi con súc sắc có thể xuất hiện một trong 6 mặt tương ứng 1,2,3,4,5,6 chấm.

Mỗi phần tử của kgm là một cặp số (x,y) $(x, y \in {1; 2; 3; 4; 5; 6})$

Lời giải:

Phép thử $T$ được xét là "Gieo một con súc sắc cân đối và đồng chất hai lần".

$Ω = {(i, j) ∣ i, j = 1, 2, 3, 4, 5, 6}$ .

Số phần tử của không gian mẫu là $n (Ω) = 36$ .

Cách liệt kê chi tiết:

Không gian mẫu:

$\begin{array}{l} Ω = {(1; 1), (1; 2), (1; 3), (1; 4), (1; 5), (1; 6), (2; 1), (2; 2), (2; 3), (2; 4), (2; 5), (2; 6), (3; 1), (3; 2), (3; 3), (3; 4), (3; 5), (3; 6), (4; 1), \\ (4; 2), (4; 3), (4; 4), (4; 5), (4; 6), (5; 1), (5; 2), (5; 3), (5; 4), (5; 5), (5; 6), (6; 1), (6; 2), (6; 3), (6; 4), (6; 5), (6; 6)} \end{array}$

Phương pháp giải:

Liệt kê và đếm số phần tử của biến cố A: $n (A), n (B)$

Lời giải:

$A$ $= (6, 4), (4, 6), (5, 5), (6, 5), (5, 6), (6, 6)$ $\Rightarrow n (A) = 6$

$B$ = $(1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 6)$ $\Rightarrow n (B) = 11$ .

Phương pháp giải:

Tính xác suất của biến cố A: $P (A) = \frac{n (A)}{n (Ω)}$ .

Lời giải:

$P (A) = \frac{n (A)}{n (Ω)}$ = $\frac{6}{36}$ = $\frac{1}{6}$ ;

$P (B)$ $= \frac{n (B)}{n (Ω)}$ = $\frac{11}{36}$ .

Bài 2 trang 74 sgk Đại số và Giải tích 11: Có bốn tấm bìa được đánh số từ

1

đến

4

. Rút ngẫu nhiên ba tấm.

a. Hãy mô tả không gian mẫu.

b. Xác định các biến cố sau:

$A$ : "Tổng các số trên ba tấm bìa bằng $8$ ";

$B$ : "Các số trên ba tấm bìa là ba số tự nhiên liên tiếp".

c. Tính $P (A), P (B)$ .
a.

Phương pháp giải:

Liệt kê và đếm số phần tử của không gian mẫu $n (Ω)$

Lời giải:

Phép thử $T$ được xét là: "Từ bốn tấm bìa đã cho, rút ngẫu nhiên ba tấm".

Không gian mẫu là:

$Ω = {(1, 2, 3), (1, 2, 4), (1, 3, 4), (2, 3, 4)}$

Số phần tử của không gian mẫu là $n (Ω) = 4$ .

Phương pháp giải:

Liệt kê và đếm các phần tử của A, B.

Lời giải:

$A = {(1, 3, 4)}$ , $n (A) = 1$

$B = (1, 2, 3), (2, 3, 4), n (B) = 2$

Phương pháp giải:

Tính xác suất của biến cố A: $P (A) = \frac{n (A)}{n (Ω)}$ .

Lời giải:

$P (A) = \frac{n (A)}{n (Ω)}$ $= \frac{1}{4};$

$P (B) = \frac{n (B)}{n (Ω)} = \frac{2}{4} = \frac{1}{2}$

Bài 3 trang 74 sgk Đại số và Giải tích 11: Một người chọn ngẫu nhiên hai chiếc giày từ bốn đôi giày cỡ khác nhau. Tính xác suất để hai chiếc chọn được tạo thành một đôi.

Phương pháp giải:

+) Tính số phần tử của không gian mẫu.

+) Tính số phần tử của biến cố: "Hai chiếc chọn được tạo thành một đôi".

+) Tính xác suất của biến cố.

Lời giải:

Phép thử $T$ được xét là: "Lấy ngẫu nhiên $2$ chiếc giày từ $4$ đôi giày có cỡ khác nhau".

Số cách lấy ra $2$ trong $8$ chiếc giày là $n (Ω) = C_{8}^{2} = 28$ (Do 2 chiếc cùng một đôi phân chia trái phải nên không giống nhau)

Gọi $A$ là biến cố: "Lấy được hai chiếc giày tạo thành một đôi".

Vì chỉ có $4$ đôi giày nên số cách lấy được $1$ trong $4$ đôi giày là $n (A) = 4$ .

Vậy $P (A)$ = $\frac{4}{28}$ = $\frac{1}{7}$

Bài 4 trang 74 sgk Đại số và Giải tích 11: Gieo một con súc sắc cân đối và đồng chất. Giả sử con súc sắc xuất hiện mặt

b

chấm. Xét phương trình

x^{2} + b x + 2 = 0

. Tính xác suất sao cho:

a. Phương trình có nghiệm

b. Phương trình vô nghiệm

c. Phương trình có nghiệm nguyên

Phương pháp giải:

Phương trình bậc hai có nghiệm $(Δ \geq 0)$ .

Lời giải:

Không gian mẫu là $Ω = {1, 2, 3, 4, 5, 6}$ , $n (Ω) = 6$

Ta có bảng:

b	1	2	3	4	5	6
∆ = b² - 8	-7	-4	1	8	17	28

Phương trình $x^{2} + b x + 2 = 0$ có nghiệm khi và chỉ khi $∆ = b^{2} - 8 \geq 0$ (*).

Vì vậy nếu $A$ là biến cố: "Xuất hiện mặt $b$ chấm sao cho phương trình $x^{2} + b x + 2 = 0$ có nghiệm"

thì $A = {3, 4, 5, 6}, n (A) = 4$ và $P (A)$ = $\frac{4}{6}$ = $\frac{2}{3}$ .

Cách khác:

Phương trình (1) có nghiệm

$\begin{array}{l} \Leftrightarrow Δ \geq 0 \Leftrightarrow b \geq 2 \sqrt 2 \\ \Rightarrow b \in {3; 4; 5; 6} . \\ \Rightarrow A = {3, 4, 5, 6} \\ \Rightarrow n (A) = 4 \end{array}$

$P (A)$ = $\frac{4}{6}$ = $\frac{2}{3}$ .

Phương pháp giải:

Phương trình bậc hai vô nghiệm $(Δ < 0)$ .

Lời giải:

Biến cố $B$ : "Xuất hiện mặt $b$ chấm sao cho phương trình $x^{2} + b x + 2 = 0$ vô nghiệm"

Dễ thấy A và B là các biến cố đối

Theo qui tắc cộng xác suất ta có $P (B) = 1 - P (A)$ = $\frac{1}{3}$ .

Cách khác:

(1) vô nghiệm

$\begin{array}{l} \Leftrightarrow Δ < 0 \Leftrightarrow b \leq 2 \sqrt 2 \\ \Rightarrow b \in {1; 2} \\ \Rightarrow B = {1, 2} \\ \Rightarrow n (B) = 2 \end{array}$

$P (B)$ $= \frac{2}{6}$ = $\frac{1}{3}$

Phương pháp giải:

Điều kiện cần để phương trình bậc hai có nghiệm nguyên là $Δ$ là số chính phương.

Lời giải:

$C$ là biến cố: "Xuất hiện mặt $b$ chấm sao cho phương trình $x^{2} + b x + 2 = 0$ có nghiệm nguyên"

Phương trình (1) có nghiệm

$\Leftrightarrow b \in {3; 4; 5; 6} .$

Thử các giá trị của b ta thấy:

Khi $b = 3$ thì phương trình trở thành $x^{2} + 3 x + 2 = 0 \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = - 2 \end{array} (t m)$

Do đó $C = {3} \Rightarrow n (C) = 1$ .

Vậy $P (C) = \frac{n (C)}{n (Ω)} = \frac{1}{6} .$

Bài 5 trang 74 sgk Đại số và Giải tích 11: Từ cỗ bài tứ lơ khơ

52

con, rút ngẫu nhiên cùng một lúc bốn con. Tính xác suất sao cho:

a. Cả bốn con đều là át;

b. Được ít nhất một con át;

c. Được hai con át và hai con.

Phương pháp giải:

Để tính xác suất của biến cố A.

+) Tính số phần tử của không gian mẫu $n (Ω)$ .

+) Tính số phần tử của biến cố A: $n (A)$

+) Tính xác suất của biến cố A: $P (A) = \frac{n (A)}{n (Ω)}$ .

Lời giải:

Phép thử $T$ được xét là: "Từ cỗ bài tú lơ khơ $52$ con bài, rút ngẫu nhiên $4$ con bài".

Mỗi kết quả có thể có là một tổ hợp chập $4$ của $52$ con bài. Do đó $n (Ω) = C_{52}^{4} = 270725$ .

Gọi biến cố $A$ : "Rút được bốn con át", $n (A) = 1$ .

Suy ra $P (A)$ = $\frac{1}{270725}$ $\approx 0, 0000037$ .

b. Gọi biến cố

B

: "Rút được ít nhất một con át". Ta có

$\bar{B}$ = "Rút được $4$ con bài đều không là át".

Mỗi kết quả có thể thuận lợi cho $\bar{B}$ là một tổ hợp chập $4$ của $48$ con bài không phải là át.

Suy ra số các kết quả có thể có thuận lợi cho $\bar{B}$ là $n (\bar{B}) = C_{48}^{4} = 194580$ .

$\Rightarrow P (\bar{B}$ ) = $\frac{194580}{270725}$ $\approx 0, 7187$ .

$\Rightarrow P (B) = 1$ - P( $\bar{B}$ ) $\approx 0, 2813$ .

Gọi

C

là biến cố: "Rút được hai con át và hai con

K

Mỗi kết quả có thể có thuận lợi cho $C$ là một tổ hợp gồm $2$ con át và $2$ con K.

Áp dụng quy tắc nhân tính được số các kết quả có thể có thuận lợi cho $C$ là

$n (C) = C_{4}^{2} . C_{4}^{2} = 6.6 = 36$ .

Vậy $P (C)$ = $\frac{36}{270725}$ $\approx 0, 000133$ .

Bài 6 trang 74 sgk Đại số và Giải tích 11: Hai bạn nam và hai bạn nữ được xếp ngồi ngẫu nhiên vào bốn ghế xếp thành hai dãy đối diện nhau. Tính xác suất sao cho:

a. Nam, nữ ngồi đối diện nhau;

b. Nữ ngồi đối diện nhau.

Phương pháp giải:

+) Mỗi cách xếp $4$ bạn vào $4$ chỗ ngồi là một hoán vị của $4$ phần tử. Tính số phần tử của không gian mẫu.

+) Gọi A là biến cố: "Nam, nữ ngồi đối diện nhau" $\Rightarrow \bar{A}$ là biến cố: "Nam đối diện nam, nữ đối diện nữ".

Tính xác suất của biến cố $\Rightarrow \bar{A}$ và sử dụng công thức $P (A) + P (\bar{A}) = 1$ .

Lời giải:

Mỗi cách xếp $4$ bạn vào $4$ chỗ ngồi là một hoán vị của $4$ phần tử, vì vậy không gian mẫu có $4! = 24$ phần tử.

Gọi A là biến cố: "Nam, nữ ngồi đối diện nhau"

$\Rightarrow \bar{A}$ là biến cố: "Nam đối diện nam, nữ đối diện nữ".

+) Có $4$ chỗ để cho bạn nữ thứ nhất chọn.

+) Có $1$ cách chọn chỗ (đối diện) cho bạn nữ thứ hai.

+) Sau khi bai bạn nữ đã chọn chỗ ngồi (đối diện nhau) thì còn lại $2$ chỗ (đối diện nhau) để xếp cho $2$ bạn nam và có $2!$ cách xếp chỗ cho $2$ bạn này.

Vi vậy theo quy tắc nhân có $4.1 .2! = 8$ cách xếp chỗ cho nam nữ không ngồi đối diện nhau.

$P$ ( $\bar{A}$ ) = $\frac{8}{24}$ = $\frac{1}{3}$ .

$\Rightarrow P (A) = 1 - P$ ( $\bar{A}$ ) = $\frac{2}{3}$ .

Phương pháp giải:

Vì chỉ có 4 người: 2 nam và 2 nữ nên nếu 2 nữ ngồi đối diện nhau thì 2 nam cũng ngồi đối diện nhau chính là biến cố $\bar{A}$ ở câu a).

Lời giải:

Vì chỉ có 4 người: 2 nam và 2 nữ nên nếu 2 nữ ngồi đối diện nhau thì 2 nam cũng ngồi đối diện nhau. Do đó biến cố này chính là biến cố $\bar{A}$ : "Nữ ngồi đối diện nhau".

Xác suất xảy ra biến cố này là $P$ ( $\bar{A}$ ) = $\frac{1}{3}$ .

Bài 7 trang 75 sgk Đại số và Giải tích 11: Có hai hộp chứa các quả cầu. Hộp thứ nhất chứa

6

quả trắng,

4

quả đen. Hộp thứ hai chứa

4

quả trắng,

6

quả đen. Từ mỗi hộp lấy ngẫu nhiên một quả. Kí hiệu:

$A$ là biến cố: "Quả lấy từ hộp thứ nhất trắng";

$B$ là biến cố: "Quả lấy từ hộp thứ hai trắng"

a. Xét xem A và B có độc lập không

b. Tính xác suất sao cho hai quả cầu lấy ra cùng màu.

c. Tính xác suất sao cho hai quả cầu lấy ra khác màu.

Phương pháp giải:

Định nghĩa hai biến cố độc lập: Hai biến cố A, B được gọi là độc lập với nhau nếu sự xảy ra của biến cố A không ảnh hưởng đến xác suất xảy ra biến cố B. A và B là hai biến cố độc lập khi và chỉ khi $P (A . B) = P (A) . P (B)$ .

Lời giải:

Phép thử $T$ được xét là: "Từ mỗi hộp lấy ngẫu nhiên một quả cầu".

Không gian mẫu là kết quả của việc lấy ngẫu nhiên 1 quả cầu ở hộp thứ nhất và một quả cầu ở hộp thứ hai

+ Có 10 cách lấy 1 quả cầu bất kì ở hộp 1 và có 10 cách lấy 1 quả cầu bất kì ở hộp 2. Nên số phần tử của không gian mẫu là;

⇒ n(Ω) = 10.10 = 100.

A: “ Quả cầu lấy từ hộp thứ nhất trắng”

⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 10 cách lấy quả cầu ở hộp B

⇒ n(A) = 6.10 = 60.

Suy ra $P (A)$ = $\frac{60}{100}$ = $0, 6$ .

B: “Quả cầu lấy từ hộp thứ hai trắng”

⇒ Có 4 cách lấy quả cầu màu trắng ở hộp B và 10 cách lấy quả cầu ở hộp A

⇒ n(B) = 4.10 = 40.

Suy ra $P (B)$ = $\frac{40}{100}$ = $0, 4$ .

A.B: “Cả hai quả cầu lấy ra đều trắng”

⇒ Có 6 cách lấy quả cầu màu trắng ở hộp A và 4 cách lấy quả cầu màu trắng ở hộp B

⇒ n(A.B) = 6.4 = 24.

Suy ra: $P (A . B)$ = $\frac{24}{100}$ = $0, 24 = 0, 6.0, 4 = P (A) . P (B)$ .

Như vậy, ta có $P (A . B) = P (A) . P (B)$ .

Suy ra $A$ và $B$ là hai biến cố độc lập với nhau.

Phương pháp giải:

Gọi C là biến cố: "Hai quả cầu lấy ra cùng màu" ta có

C = A . B

\bar{A}

\bar{B}

. Với

\bar{A}; \bar{B}

lần lượt là các biến cố đối của biến cố A và B.

Lời giải:

Gọi

C

là biến cố: "Lấy được hai quả cầu cùng màu". Ta có

$C = A . B$ + $\bar{A}$ . $\bar{B}$ .

Trong đó $\bar{A}$ = "Quả cầu lấy từ hộp thứ nhất có màu đen" và $P$ ( $\bar{A}$ ) = $0, 4$ .

$\bar{B}$ : "Quả cầu lấy từ hộp thứ hai có màu đen" và P( $\bar{B}$ ) = $0, 6$ .

Và ta có $A . B$ và $\bar{A}$ . $\bar{B}$ là hai biến cố xung khắc với nhau.

$A$ và $B$ độc lập với nhau, nên $\bar{A}$ và $\bar{B}$ cũng độc lập với nhau.

Qua trên suy ra;

$P (C) = P$ ( $A . B$ + $\bar{A}$ . $\bar{B}$ )

$= P (A . B)$ + $P$ ( $\bar{A}$ . $\bar{B}$ ) = $P (A) . P (B)$ + $P$ ( $\bar{A}$ ). $P$ ( $\bar{B}$ )

$= 0, 6.0, 4 + 0, 4.0, 6 = 0, 48$ .

Phương pháp giải:

Gọi D là biến cố: "Hai quả cầu lấy ra khác màu" ta có

D = \bar{C}

Lời giải:

Gọi $D$ là biến cố: "Lấy được hai quả cầu khác màu". Ta có

$D = \bar{C} \Rightarrow P (D) = 1 - P (C) = 1 - 0, 48 = 0, 52$ .

Lý thuyết Bài Xác suất và biến cố

1. Định nghĩa cổ điển của xác suất

Giả sử $A$ là biến cố liên quan đến phép thử $T$ và phép thử $T$ có một số hữu hạn kết quả có thể có, đồng khả năng. Khi đó ta gọi tỉ số $\frac{n (A)}{n (Ω)}$ là xác suất của biến cố $A$ , kí hiệu là

$P (A)$ = $\frac{n (A)}{n (Ω)}$

Trong đó,

+) $n (A)$ là số phần tử của tập hợp $A$ , cũng chính là số các kết quả có thể có của phép thử $T$ thuận lợi cho biến cố $A$ ;

+) $n (Ω)$ là số phần tử của không gian mẫu $Ω$ , cũng chính là số các kết quả có thể có của phép thử $T$ .

Ví dụ:

Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất. Tính xác suất để mặt xuất hiện là mặt có số chia hết cho $3$ .

Hướng dẫn:

Không gian mẫu $Ω = {1; 2; 3; 4; 5; 6}$

$\Rightarrow n (Ω) = 6$ .

Biến cố $A :$ Mặt xuất hiện có số chia hết cho $3$ .

Khi đó $A = {3; 6}$

$\Rightarrow n (A) = 2$ .

Vậy xác suất $P (A) = \frac{n (A)}{n (Ω)} = \frac{2}{6} = \frac{1}{3}$ .

2. Các tính chất cơ bản của xác suất

2.1 Định lí

a) $P (ϕ) = 0; P (Ω) = 1$ .

b) $0 \leq P (A) \leq 1$ , với mọi biến cố $A$ .

c) Nếu $A$ và $B$ xung khắc với nhau, thì ta có

$P (A \cup B) = P (A) + P (B)$ (công thức cộng xác suất).

2.2 Hệ quả

Với mọi biến cố $A$ , ta luôn luôn có: $P$ ( $\bar{A}$ ) = $1 - P (A)$ .

3. Hai biến cố độc lập

Định nghĩa

Hai biến cố (liên quan đến cùng một phép thử) là độc lập với nhau khi và chỉ khi việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng đến xác suất xảy ra của biến cố kia (nói cách khác là không làm ảnh hưởng đến khả năng xảy ra của biến cố kia).

Định lý

Nếu $A, B$ là hai biến cố (liên quan đến cùng một phép thử) sao cho $P (A) > 0$ ,

$P (B) > 0$ thì ta có:

a) $A$ và $B$ là hai biến cố độc lập với nhau khi và chỉ khi:

$P (A . B) = P (A) . P (B)$

Chú ý: Kết quả vừa nêu chỉ đúng trong trường hợp khảo sát tính độc lập chỉ của 2 biến cố.

b) Nếu $A$ và $B$ độc lập với nhau thì các cặp biến cố sau đây cũng độc lập với nhau:

$A$ và $\bar{B}$ , $\bar{A}$ và $B$ , $\bar{A}$ và $\bar{B}$ .

Ví dụ:

Gieo một con súc sắc cân đối và đồng chất hai lần. Tính xác suất các biến cố sau:

$A :$ “Lần thứ nhất xuất hiện mặt $4$ chấm”

$B :$ “Lần thứ hai xuất hiện mặt $4$ chấm”

Từ đó suy ra hai biến cố $A$ và $B$ độc lập.

Hướng dẫn

Không gian mẫu: $Ω = {(i; j), i, j \in Z, 1 \leq i \leq 6, 1 \leq j \leq 6}$

$\Rightarrow n (Ω) = 6.6 = 36$ .

Biến cố $A :$ “Lần thứ nhất xuất hiện mặt $4$ chấm”

$A = {(4; 1), (4; 2), (4; 3), (4; 4), (4; 5), (4; 6)}$

$\Rightarrow n (A) = 6$

$\Rightarrow P (A) = \frac{n (A)}{n (Ω)} = \frac{6}{36} = \frac{1}{6}$ .

Biến cố $B :$ “Lần thứ hai xuất hiện mặt $4$ chấm”

$B = {(1; 4), (2; 4), (3; 4), (4; 4), (5; 4), (6; 4)}$

$\Rightarrow n (B) = 6$

$\Rightarrow P (B) = \frac{n (B)}{n (Ω)} = \frac{6}{36} = \frac{1}{6}$ .

Gọi $C = A . B$ là biến cố: “Cả hai lần đều xuất hiện mặt $4$ chấm”.

Khi đó $C = {(4; 4)}$

$\Rightarrow P (A . B) = \frac{n (C)}{n (Ω)} = \frac{1}{36}$ .

Dễ thấy $P (A . B) = P (A) . P (B)$ nên $A, B$ là hai biến cố độc lập.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Toán Học Lớp 11

Giải Toán 11 Bài 5: Xác suất của biến cố

Xem thêm các chương trình khác: