Chúng tôi giới thiệu Giải bài tập Toán 11 Bài 1: Định nghĩa và ý nghĩa của đạo hàm chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Định nghĩa và ý nghĩa của đạo hàm lớp 11.
Giải bài tập Toán 11 Bài 1: Định nghĩa và ý nghĩa của đạo hàm
Hãy tính vận tốc trung bình của chuyển động trong khoảng với và
Nêu nhận xét về những kết quả thu được khi càng gần .
Lời giải:
Vận tốc của đoàn tàu là:
Vận tốc trung bình của chuyển động trong khoảng với:
càng gần thì vận tốc trung bình của chuyển động trong khoảng càng gần 3.
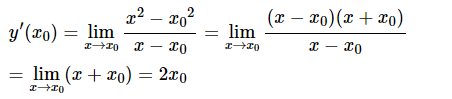
- Giả sử Δx là số gia của đối số tại x0=1. Ta có:
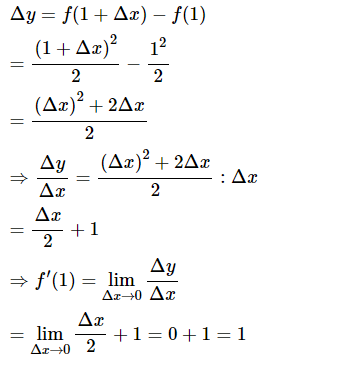
c.
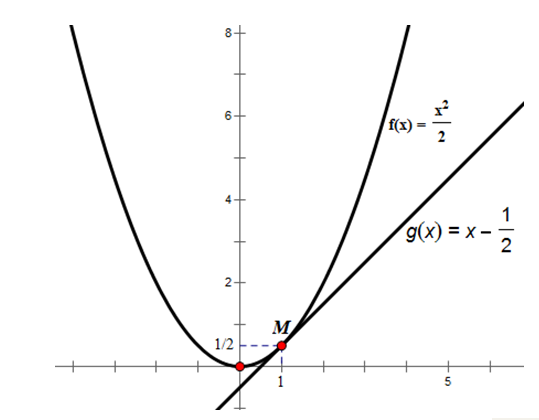
- Đường thẳng có hệ số góc bằng có dạng:
hay
Mà đường thẳng đó đi qua điểm ) nên có:
⇒ đường thẳng đi qua và có hệ số góc bằng là:
Ta có đồ thị như trên. Đường thẳng tiếp xúc với đồ thị hàm số tại
- Tính theo số gia .
- Tính tỉ số và tính đạo hàm .
Lời giải:
- Giả sử là số gia của đối số tại . Ta có:
- Tính theo .
- Tính tỉ số .
- Tính giới hạn và kết luận.
Lời giải:
a.
Giả sử là số gia của đối số tại bất kỳ. Ta có:
b.
Giả sử là số gia của đối số tại bất kỳ. Ta có:
a.
b.
a.
Phương pháp giải:
Số gia của hàm số là:
Lời giải:
b.
Phương pháp giải:
Số gia của hàm số là:
Lời giải:
a.
b. y = x2 -1
c. y = 2x3
d. y =
Sử dụng công thức: tính , từ đó suy ra
(Trong công thức ta coi )
Lời giải:
a.
b.
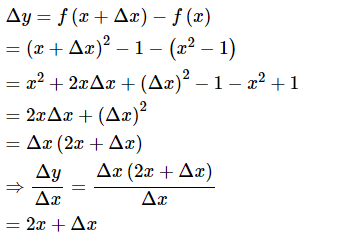
c.
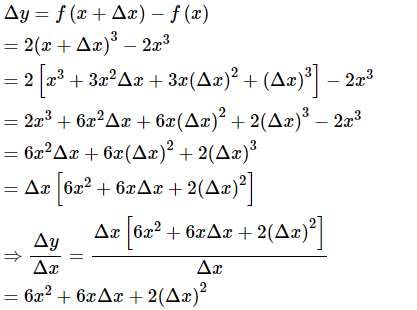
d.
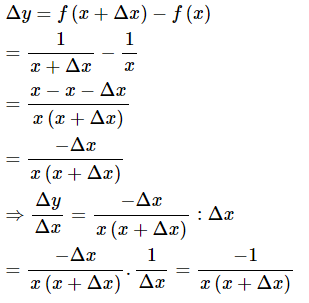
Bài 3 trang 156 sgk Đại số và Giải tích 11: Tính (bằng định nghĩa) đạo hàm của mỗi hàm số sau tại các điểm đã chỉ ra:
a. tại
b. y = tại x0 = 2
c. y = tại x0 = 2
Bước 1: Giả sử là số gia của đối số tại , tính .
Bước 2: Lập tỉ số .
Bước 3: Tìm .
Kết luận .
Lời giải:
a.
Giả sử là số gia của số đối tại . Ta có:
Vậy .
Cách khác:
b.
Giả sử là số gia của số đối tại . Ta có:
Vậy .
Cách khác:
c.
Giả sử là số gia của số đối tại .Ta có:
Vậy .
Cách khác:
không có đạo hàm tại điểm nhưng có đạo hàm tại điểm .
Điều kiện cần để hàm số có đạo hàm tại điểm là hàm số liên tục tại .
Sử dụng định nghĩa chứng minh hàm số có đạo hàm tại :
Cho hàm số xác định trên khoảng và . Nếu tồn tại giới hạn (hữu hạn) thì tồn tại đạo hàm của hàm số tại .
Lời giải:
Ta có:
Do đó hàm số gián đoạn tại .
Vậy hàm số không có đạo hàm tại điểm (vi phạm điều kiện cần).
Xét giới hạn:
Vậy hàm số có đạo hàm tại và .
a. Tại điểm có tọa độ
b. Tại điểm có hoành độ bằng 2
c. Biết hệ số góc của tiếp tuyến bằng 3
a.
Phương pháp giải:
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là:
Lời giải:
Ta có:
Ta có: .
Vậy phương trình tiếp tuyến tại điểm là:
b.
Phương pháp giải:
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là:
Lời giải:
Ta có: , .
Vậy phương trình tiếp tuyến tại điểm có hoành độ bằng là: .
c.
Phương pháp giải:
Hệ số góc của tiếp tuyến tại điểm có hoành độ là .
Giải phương trình tìm , từ đó viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ .
Lời giải:
Gọi là hoành độ tiếp điểm. Ta có:
.
+) Với ta có , phương trình tiếp tuyến là
+) Với ta có , phương trình tiếp tuyến là
a. Tại điểm
b. Tại điểm có hoành độ bằng -1;
c. Biết rằng hệ số góc của tiếp tuyến bằng
a.
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là:
Lời giải:
Xét giới hạn:
Ta có: .
Vậy phương trình tiếp tuyến của hypebol tại điểm là
b.
Phương pháp giải:
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là:
Lời giải:
Ta có: .
Vậy phương trình tiếp tuyến tại điểm có hoành độ là là: .
c.
Phương pháp giải:
Hệ số góc của tiếp tuyến tại điểm có hoành độ là .
Giải phương trình tìm , từ đó viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ .
Lời giải:
Gọi là hoành độ tiếp điểm. Ta có
.
Với ta có , phương trình tiếp tuyến là .
Với ta có , phương trình tiếp tuyến là: .
Chú ý: Trong các ý a, b, c đều sử dụng cách tính đạo hàm của hàm số tại điểm bằng định nghĩa. Sau khi học xong bài 2 thì các em có thể quay lại làm lại bài tập này, việc tính đạo hàm sẽ dễ hơn rất nhiều
a. Tìm vận tốc trung bình của chuyển động trong khoảng thời gian từ t (t = 5s) đến , trong các trường hợp .
b. Tính vận tốc tức thời của chuyển động tại thời điểm t =5s
Vận tốc trung bình của chuyển động trong khoảng thời gian từ đến là
Lời giải:
a.
Vận tốc trung bình của chuyển động trong khoảng thời gian từ đến là
Với và
+) thì ;
+) thì ;
+) thì .
b.
Vận tốc tức thời của chuyển động tại thời điểm chính là vận tốc trung bình trong khoảng thời gian khi là :
Lý thuyết Bài Định nghĩa và ý nghĩa của đạo hàm
1. Định nghĩa
Cho hàm số xác định trên khoảng , . Giới hạn hữu hạn (nếu có) của tỉ số khi được gọi là đạo hàm của hàm số đã cho tại , kí hiệu là hay . Như vậy:
Nếu đặt và thì ta có
Đại lượng được gọi là số gia của đối số tại và đại lượng được gọi là số gia tương ứng của hàm số.
2. Quy tắc tính đạo hàm bằng định nghĩa
Bước 1. Với là số gia của số đối tại ,tính ;
Bước 2. Lập tỉ số ;
Bước 3. Tính .
Nhận xét: nếu thay bởi ta có định nghĩa và quy tắc tính đạo hàm của hàm số tại điểm .
3. Quan hệ giữa tính liên tục và sự tồn tại đạo hàm
Định lí. Nếu hàm số có đạo hàm tại thì nó liên tục tại .
Chú ý.
Định lí trên tương đương với khẳng định : Nếu gián đoạn tại thì nó không có đạo hàm tại điểm đó.
Mệnh đề đảo của định lí không đúng. Một hàm số liên tục tại một điểm có thể không có đạo hàm tại điểm đó.
4. Ý nghĩa hình học của đạo hàm
Nếu tồn tại, là hệ số góc của tiếp tuyến của đồ thị hàm số tại điểm . Khi đó phương trình tiếp tuyến của đồ thị tại điểm là
5. Ý nghĩa vật lí của đạo hàm
là vận tốc tức thời của chuyển động tại thời điểm .

