Giải Toán 11 Bài 3: Đạo hàm của hàm số lượng giác

59 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Toán 11 Bài 3: Đạo hàm của hàm số lượng giác chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Đạo hàm của hàm số lượng giác lớp 11.

Giải bài tập Toán 11 Bài 3: Đạo hàm của hàm số lượng giác

Trả lời câu hỏi giữa bài

Trả lời hoạt động 1 trang 163 sgk Đại số và Giải tích 11: Tính

\frac{\sin 0, 01}{0, 01}; \frac{\sin 0, 001}{0, 001}

bằng máy tính bỏ túi.

Lời giải:

Trả lời hoạt động 2 trang 165 sgk Đại số và Giải tích 11: Tính đạo hàm của hàm số:

y = \sin (\frac{π}{2} - x)

Phương pháp giải:

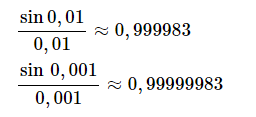
Cách 1: chuyển $\sin (\frac{π}{2} - x)$ thành $\cos x$ rồi tính đạo hàm.

Cách 2: Hàm hợp $y = y (u (x))$ có đạo hàm: $y = y_{u}^{'} . u_{x}^{'}$

Lời giải:

$y = \sin (\frac{π}{2} - x)$

Cách 1:

Ta có: $\sin (\frac{π}{2} - x) = \cos x$ (do góc $\frac{π}{2} - x$ và $x$ phụ nhau.)

$\Rightarrow y = \sin (\frac{π}{2} - x) = \cos x$

$\Rightarrow y^{'} = \cos^{'} x = - \sin x$

Cách 2:

Đặt $u = \frac{π}{2} - x$ thì $y = \sin u$ và $u_{x}^{'} = - 1; y_{u}^{'} = \sin^{'} u = \cos u$ .

Áp dụng đạo hàm hàm hợp ta có:

$y^{'} = y_{u}^{'} . u_{x}^{'} = \cos u . (- 1) = (- 1) . c o s (\frac{π}{2} - x) = - \sin x$

(do $c o s (\frac{π}{2} - x) = s i n x) .$

Trả lời hoạt động 3 trang 166 sgk Đại số và Giải tích 11: Tính đạo hàm của hàm số:

$f (x) = \frac{\sin x}{\cos x} (x \neq \frac{π}{2} + k π; k \in Z)$

Phương pháp giải:

Áp dụng: ${(\frac{u}{v})}^{^{^{'}}}$ = $\frac{u^{'} v - u v^{'}}{v^{2}},$

với $u = \sin x; v = \cos x$

Lời giải:

$\begin{aligned} f^{'} (x) = (\frac{\sin x}{\cos x})^{'} = \frac{(\sin x)^{'} \cos x - \sin x . (\cos x)^{'}}{\cos^{2} x} \\ = \frac{\cos^{2} x + \sin^{2} x}{\cos^{2} x} = \frac{1}{\cos^{2} x} \end{aligned}$

Trả lời hoạt động 4 trang 167 sgk Đại số và Giải tích 11: Tính đạo hàm của hàm số:

$y = \tan (\frac{π}{2} - x)$ với $x \neq k π, k \in Z$

Phương pháp giải:

Cách 1: Đưa về $y = \tan (\frac{π}{2} - x) = \cot x$ rồi tính đạo hàm.

Cách 2: Sử dụng công thức tính đạo hàm hàm hợp với $y = \tan u; u = \frac{π}{2} - x$

Lời giải:

Cách 1:

Vì $\frac{π}{2} - x$ và $x$ là hai góc phụ nhau nên $\tan (\frac{π}{2} - x) = \cot x$

$\Rightarrow y^{'} = \tan^{'} (\frac{π}{2} - x) = \cot^{'} x = \frac{- 1}{\sin^{2} x}$ .

Cách 2:

Đặt $u = \frac{π}{2} - x$ thì $y = \tan u \Rightarrow y^{'} = \tan^{'} u . u_{x}^{'}$

Mà $\tan^{'} u = \frac{1}{\cos^{2} u}; u_{x}^{'} = (\frac{π}{2} - x)^{'} = - 1.$

$\Rightarrow y^{'} = \frac{1}{\cos^{2} u} . (- 1) = \frac{- 1}{\cos^{2} u} = \frac{- 1}{\cos^{2} (\frac{π}{2} - x)} = \frac{- 1}{\sin^{2} x}$ (do cos⁡( $\frac{π}{2} - x) = s i n x)$

Bài tập (trang 168, 169 sgk Đại số và Giải tích 11)

Bài 1 trang 168 sgk Đại số và Giải tích 11: Tìm đạo hàm của các hàm số sau:

a. $y = \frac{x - 1}{5 x - 2}$

b. $y = \frac{2 x + 3}{7 - 3 x}$

c. $y = \frac{x^{2} + 2 x + 3}{3 - 4 x}$

d. $y = \frac{x^{2} + 7 x + 3}{x^{2} - 3 x}$

Phương pháp giải:

Áp dụng quy tắc tính đạo hàm của một thương ${(\frac{u}{v})}^{'} = \frac{u^{'} v - u v^{'}}{v^{2}}$ với $u = x - 1; v = 5 x - 2$

Lời giải:

$\begin{array}{l} y = \frac{x - 1}{5 x - 2} \\ \Rightarrow y^{'} = \frac{{(x - 1)}^{'} (5 x - 2) - (x - 1) {(5 x - 2)}^{'}}{{(5 x - 2)}^{2}} \\ y^{'} = \frac{(5 x - 2) - 5 (x - 1)}{{(5 x - 2)}^{2}} \\ y^{'} = \frac{5 x - 2 - 5 x + 5}{{(5 x - 2)}^{2}} \\ y^{'} = \frac{3}{{(5 x - 2)}^{2}} \end{array}$

Phương pháp giải:

Áp dụng quy tắc tính đạo hàm của một thương ${(\frac{u}{v})}^{'} = \frac{u^{'} v - u v^{'}}{v^{2}}$ với $u = 2 x + 3; v = 7 - 3 x$

Lời giải:

$\begin{array}{l} y = \frac{2 x + 3}{7 - 3 x} \\ \Rightarrow y^{'} = \frac{{(2 x + 3)}^{'} (7 - 3 x) - (2 x + 3) {(7 - 3 x)}^{'}}{{(7 - 3 x)}^{2}} \\ y^{'} = \frac{2 (7 - 3 x) - (2 x + 3) (- 3)}{{(7 - 3 x)}^{2}} \\ y^{'} = \frac{2 (7 - 3 x) + 3 (2 x + 3)}{{(7 - 3 x)}^{2}} \\ y^{'} = \frac{14 - 6 x + 6 x + 9}{{(7 - 3 x)}^{2}} \\ y^{'} = \frac{23}{{(7 - 3 x)}^{2}} \end{array}$

Phương pháp giải:

Áp dụng quy tắc tính đạo hàm của một thương ${(\frac{u}{v})}^{'} = \frac{u^{'} v - u v^{'}}{v^{2}}$ với $u = x^{2} + 2 x + 3; v = 3 - 4 x$

Lời giải:

$\begin{array}{l} y = \frac{x^{2} + 2 x + 3}{3 - 4 x} \\ y^{'} = \frac{{(x^{2} + 2 x + 3)}^{'} (3 - 4 x) - (x^{2} + 2 x + 3) {(3 - 4 x)}^{'}}{{(3 - 4 x)}^{2}} \\ y^{'} = \frac{(2 x + 2) (3 - 4 x) - (x^{2} + 2 x + 3) (- 4)}{{(3 - 4 x)}^{2}} \\ = \frac{6 x - 8 x^{2} + 6 - 8 x + 4 x^{2} + 8 x + 12}{{(3 - 4 x)}^{2}} \\ = \frac{- 4 x^{2} + 6 x + 18}{{(3 - 4 x)}^{2}} \end{array}$

Phương pháp giải:

Áp dụng quy tắc tính đạo hàm của một thương ${(\frac{u}{v})}^{'} = \frac{u^{'} v - u v^{'}}{v^{2}}$ với $u = x^{2} + 7 x + 3; v = x^{2} - 3 x$

Lời giải:

$\begin{array}{l} y = \frac{x^{2} + 7 x + 3}{x^{2} - 3 x} \\ \Rightarrow y^{'} = \frac{{(x^{2} + 7 x + 3)}^{'} (x^{2} - 3 x) - (x^{2} + 7 x + 3) {(x^{2} - 3 x)}^{'}}{{(x^{2} - 3 x)}^{2}} \\ y^{'} = \frac{(2 x + 7) (x^{2} - 3 x) - (x^{2} + 7 x + 3) (2 x - 3)}{{(x^{2} - 3 x)}^{2}} \\ = \frac{2 x^{3} - 6 x^{2} + 7 x^{2} - 21 x - 2 x^{3} - 14 x^{2} - 6 x + 3 x^{2} + 21 x + 9}{{(x^{2} - 3 x)}^{2}} \\ = \frac{- 10 x^{2} - 6 x + 9}{{(x^{2} - 3 x)}^{2}} \end{array}$

Bài 2 trang 168 sgk Đại số và Giải tích 11: Giải các bất phương trình sau:

a. $y^{'} < 0$ với $y = \frac{x^{2} + x + 2}{x - 1}$

b. $y^{'} \geq 0$ với $y = \frac{x^{2} + 3}{x + 1}$

c. $y^{'} > 0$ với $y = \frac{2 x - 1}{x^{2} + x + 4}$

Phương pháp giải:

Sử dụng quy tắc đạo hàm của 1 thương và bảng đạo hàm các hàm số cơ bản, tính đạo hàm của các hàm số và giải bất phương trình.

Lời giải:

Ta có $y^{'} = \frac{(x^{2} + x + 2)^{'} . (x - 1) - (x^{2} + x + 2) . (x - 1)^{'}}{(x - 1)^{2}}$

$= \frac{(2 x + 1) (x - 1) - (x^{2} + x + 2) .1}{{(x - 1)}^{2}}$

$= \frac{2 x^{2} + x - 2 x - 1 - x^{2} - x - 2}{{(x - 1)}^{2}}$

$= \frac{x^{2} - 2 x - 3}{(x - 1)^{2}}$

Do đó, $y^{'} < 0 \Leftrightarrow \frac{x^{2} - 2 x - 3}{(x - 1)^{2}} < 0$

$\Leftrightarrow {\begin{cases} x \neq 1 \\ x^{2} - 2 x - 3 < 0 \end{cases}$

$\Leftrightarrow {\begin{matrix} x \neq 1 \\ - 1 < x < 3 \end{matrix}$

$\Leftrightarrow$ $x \in (- 1; 1) \cup (1; 3)$ .

Ta có $y^{'} = \frac{(x^{2} + 3)^{'} . (x + 1) - (x^{2} + 3) . (x + 1)^{'}}{(x + 1)^{2}}$

$= \frac{2 x (x + 1) - (x^{2} + 3) .1}{{(x + 1)}^{2}}$ $= \frac{2 x^{2} + 2 x - x^{2} - 3}{{(x + 1)}^{2}}$

= $\frac{x^{2} + 2 x - 3}{(x + 1)^{2}}$ .

Do đó, $y^{'} \geq 0 \Leftrightarrow \frac{x^{2} + 2 x - 3}{(x + 1)^{2}} \geq 0$

$\Leftrightarrow {\begin{cases} x + 1 \neq 0 \\ x^{2} + 2 x - 3 \geq 0 \end{cases}$

$\Leftrightarrow {\begin{matrix} x \neq - 1 \\ [\begin{matrix} x \geq 1 \\ x \leq - 3 \end{matrix} \end{matrix} \Leftrightarrow [\begin{matrix} x \geq 1 \\ x \leq - 3 \end{matrix}$

$\Leftrightarrow x \in (- \infty; - 3] \cup [1; + \infty)$ .

Ta có $y^{'} = \frac{(2 x - 1)^{'} . (x^{2} + x + 4) - (2 x - 1) . (x^{2} + x + 4)^{'}}{(x^{2} + x + 4)^{2}}$

$= \frac{2 (x^{2} + x + 4) - (2 x - 1) (2 x + 1)}{{(x^{2} + x + 4)}^{2}}$ $= \frac{2 x^{2} + 2 x + 8 - 4 x^{2} + 2 x - 2 x + 1}{{(x^{2} + x + 4)}^{2}}$

$= \frac{- 2 x^{2} + 2 x + 9}{(x^{2} + x + 4)^{2}}$ .

Do đó, $y^{'} > 0 \Leftrightarrow \frac{- 2 x^{2} + 2 x + 9}{(x^{2} + x + 4)^{2}} > 0 \Leftrightarrow - 2 x^{2} + 2 x + 9 > 0$ $\Leftrightarrow \frac{1 - \sqrt{19}}{2} < x < \frac{1 + \sqrt{19}}{2} \Leftrightarrow x \in (\frac{1 - \sqrt{19}}{2}; \frac{1 + \sqrt{19}}{2})$

Vì $x^{2} + x + 4 =$ ${(x + \frac{1}{2})}^{2}$ + $\frac{15}{4} > 0$ , với $\forall x \in R$ .

Bài 3 trang 169 sgk Đại số và Giải tích 11: Tìm đạo hàm của các hàm số sau:

$\begin{array}{l} a) y = 5 \sin x - 3 \cos x \\ b) y = \frac{\sin x + \cos x}{\sin x - \cos x} \\ c) y = x \cot x \\ d) y = \frac{\sin x}{x} + \frac{x}{\sin x} \\ e) y = \sqrt{1 + 2 \tan x} \\ f) y = \sin \sqrt{1 + x^{2}} \end{array}$

Phương pháp giải:

Sử dụng các công thức tính đạo hàm của các hàm lượng giác:

$\begin{array}{l} {(\sin x)}^{'} = \cos x, {(\cos x)}^{'} = - \sin x, \\ {(\tan x)}^{'} = \frac{1}{\cos^{2} x}, {(\cot x)}^{'} = - \frac{1}{\sin^{2} x} \end{array}$

Sử dụng các quy tắc tính đạo hàm của 1 tích, 1 thương và quy tắc tính đạo hàm hàm số hợp.

Lời giải:

Bài 4 trang 168 sgk Đại số và Giải tích 11: Tìm đạo hàm của các hàm số sau:

$\begin{array}{l} a) y = (9 - 2 x) (2 x^{3} - 9 x^{2} + 1) \\ b) y = (6 \sqrt{x} - \frac{1}{x^{2}}) (7 x - 3) \\ c) y = (x - 2) \sqrt{x^{2} + 1} \\ d) y = \tan^{2} x - \cot x^{2} \\ e) y = \cos \frac{x}{1 + x} \end{array}$

Phương pháp giải:

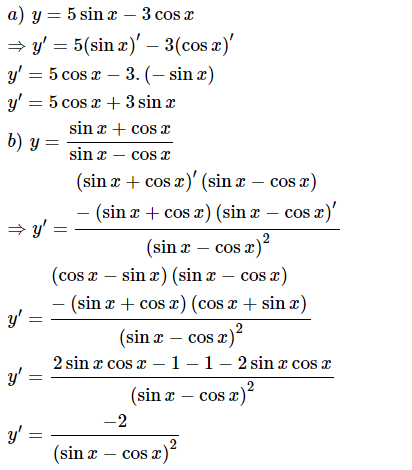
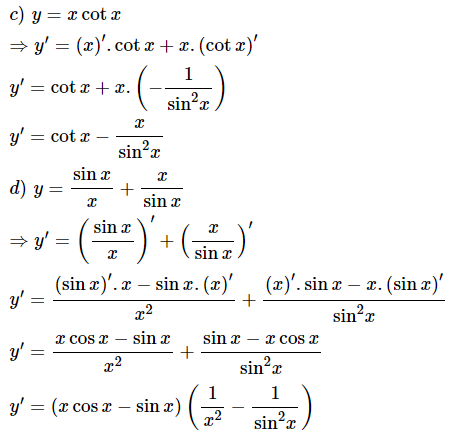
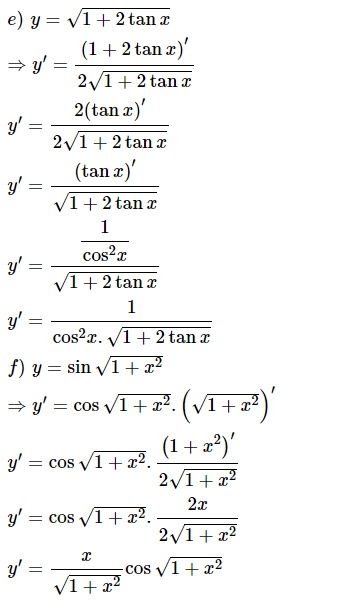
Sử dụng các quy tắc tính đạo hàm của tích, thương, quy tắc tính đạo hàm hàm số hợp và bảng đạo hàm cơ bản.

Lời giải:

Bài 5 trang 168 sgk Đại số và Giải tích 11 Tính

\frac{f^{'} (1)}{φ^{'} (1)}

, biết rằng

f (x) = x^{2}

và

φ (x) = 4 x + \sin \frac{π x}{2}

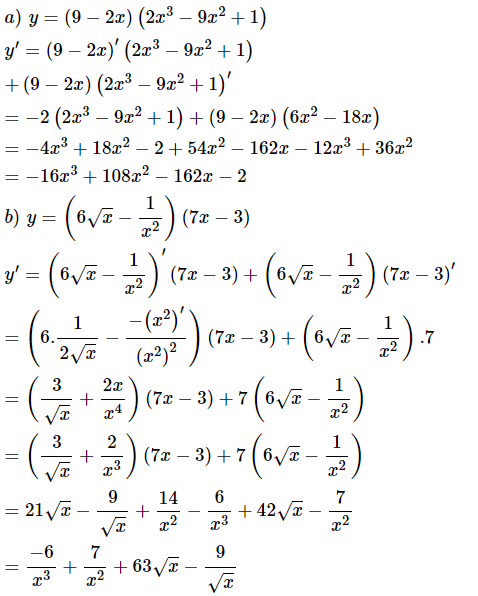
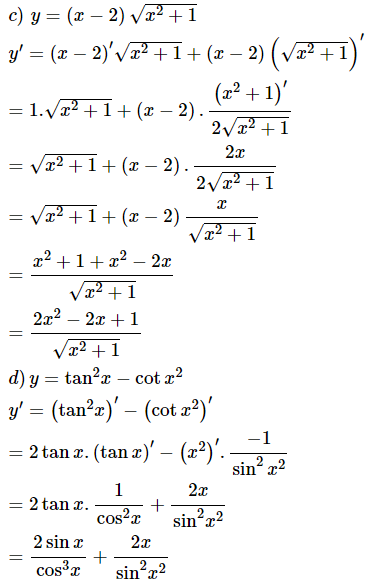
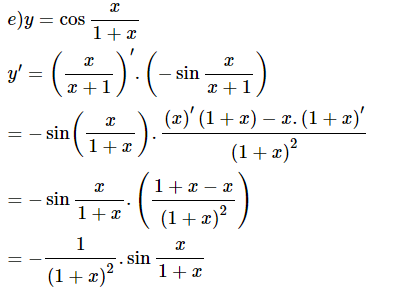
Phương pháp giải:

+) Tính $f^{'} (x)$ và $φ^{'} (x)$

+) Suy ra $f^{'} (1)$ và $φ^{'} (1)$ và $\frac{f^{'} (1)}{φ^{'} (1)}$ .

Lời giải:

Ta có:

$\begin{array}{l} f (x) = x^{2} \\ \Rightarrow f^{'} (x) = {(x^{2})}^{'} = 2 x \\ \Rightarrow f^{'} (1) = 2.1 = 2 \\ φ (x) = 4 x + \sin \frac{π x}{2} \\ \Rightarrow φ^{'} (x) = {(4 x + \sin \frac{π x}{2})}^{'} \\ = {(4 x)}^{'} + {(\sin \frac{π x}{2})}^{'} \\ = 4 + {(\frac{π x}{2})}^{'} \cos \frac{π x}{2} \\ = 4 + \frac{π}{2} \cos \frac{π x}{2} \\ \Rightarrow φ^{'} (1) = 4 + \frac{π}{2} \cos \frac{π .1}{2} \\ = 4 + \frac{π}{2} .0 = 4 \\ \Rightarrow \frac{f^{'} (1)}{φ^{'} (1)} = \frac{2}{4} = \frac{1}{2} \end{array}$

Bài 6 trang 168 sgk Đại số và Giải tích 11: Chứng minh rằng các hàm số sau có đạo hàm không phụ thuộc

x

a. $\sin^{6} x + \cos^{6} x + 3 \sin^{2} x . \cos^{2} x$

b. $\cos^{2} (\frac{π}{3} - x) + \cos^{2} (\frac{π}{3} + x) + \cos^{2} (\frac{2 π}{3} - x)$ $+ \cos^{2} (\frac{2 π}{3} + x) - 2 \sin^{2} x$

Phương pháp giải:

Tính đạo hàm của các hàm số đã cho và rút gọn.

Lời giải:

Ta có:

$\begin{array}{l} y^{'} = {(\sin^{6} x)}^{'} + {(\cos^{6} x)}^{'} + {(3 \sin^{2} x \cos^{2} x)}^{'} \\ = 6 \sin^{5} x {(\sin x)}^{'} + 6 \cos^{5} x {(\cos x)}^{'} \\ + 3. [{(\sin^{2} x)}^{'} \cos^{2} x + \sin^{2} x {(\cos^{2} x)}^{'}] \\ = 6 \sin^{5} x \cos x + 6 \cos^{5} x (- \sin x) \\ + 3 [2 \sin x \cos x \cos^{2} x + \sin^{2} x .2 \cos x (- \sin x)] \\ = 6 \sin^{5} x \cos x - 6 \cos^{5} x \sin x \\ + 6 \sin x \cos^{3} x - 6 \cos x \sin^{3} x \\ = (6 \sin^{5} x \cos x - 6 \cos x \sin^{3} x) \\ + 6 \sin x \cos^{3} x - 6 \cos^{5} x \sin x \\ = 6 \sin^{3} x \cos x (\sin^{2} x - 1) \\ + 6 \sin x \cos^{3} x (1 - \cos^{2} x) \\ = 6 \sin^{3} x \cos x . (- \cos^{2} x) \\ + 6 \sin x \cos^{3} x \sin^{2} x \\ = - 6 \sin^{3} x \cos^{3} x + 6 \sin^{3} x \cos^{3} x \\ = 0 \\ \Rightarrow y^{'} = 0, \forall x \end{array}$

Vậy $y^{'} = 0$ với mọi $x$ , tức là $y^{'}$ không phụ thuộc vào $x$ .

Cách khác:

$\begin{array}{l} \sin^{6} x + \cos^{6} x \\ = {(\sin^{2} x)}^{3} + {(\cos^{2} x)}^{3} \\ = {(\sin^{2} x + \cos^{2} x)}^{3} - 3 \sin^{2} x \cos^{2} x (\sin^{2} x + \cos^{2} x) \\ = 1^{3} - 3 \sin^{2} x \cos^{2} x .1 \\ = 1 - 3 \sin^{2} x \cos^{2} x \\ \Rightarrow y = \sin^{6} x + \cos^{6} x + 3 \sin^{2} x \cos^{2} x = 1 \\ \Rightarrow y^{'} = {(1)}^{'} = 0 \end{array}$

Phương pháp giải:

Sử dụng các công thức biến đổi tổng thành tích: $\sin x - \sin y = 2 \cos \frac{x + y}{2} \sin \frac{x - y}{2}$

Lời giải:

$y = \frac{1 + \cos (\frac{2 π}{3} - 2 x)}{2} + \frac{1 + \cos (\frac{2 π}{3} + 2 x)}{2} + \frac{1 + \cos (\frac{4 π}{3} - 2 x)}{2}$

$+ \frac{1 + \cos (\frac{4 π}{3} + 2 x)}{2} - 2 \sin^{2} x$

$= \frac{1}{2} + \frac{1}{2} \cos (\frac{2 π}{3} - 2 x)$ $+ \frac{1}{2} + \frac{1}{2} \cos (\frac{2 π}{3} + 2 x)$ $+ \frac{1}{2} + \frac{1}{2} \cos (\frac{4 π}{3} - 2 x)$ $+ \frac{1}{2} + \frac{1}{2} \cos (\frac{4 π}{3} + 2 x)$ $- 2. \frac{1 - \cos 2 x}{2}$

$= 1 + \frac{1}{2} \cos (\frac{2 π}{3} - 2 x)$ $+ \frac{1}{2} \cos (\frac{2 π}{3} + 2 x)$ $+ \frac{1}{2} \cos (\frac{4 π}{3} - 2 x)$ $+ \frac{1}{2} \cos (\frac{4 π}{3} + 2 x)$ $+ \cos 2 x$

Do đó $y^{'} = \frac{1}{2} . (- 2) . [- \sin (\frac{2 π}{3} - 2 x)]$ $+ \frac{1}{2} .2 . [- \sin (\frac{2 π}{3} + 2 x)]$ $+ \frac{1}{2} . (- 2) . [- \sin (\frac{4 π}{3} - 2 x)]$ $+ \frac{1}{2} .2 . [- \sin (\frac{4 π}{3} + 2 x)]$ $- 2 \sin 2 x$

$= \sin (\frac{2 π}{3} - 2 x) - \sin (\frac{2 π}{3} + 2 x) + \sin (\frac{4 π}{3} - 2 x)$ $- \sin (\frac{4 π}{3} + 2 x) - 2 \sin 2 x$

$= 2 \cos \frac{2 π}{3} . \sin (- 2 x) + 2 \cos \frac{4 π}{3} . \sin (- 2 x) - 2 \sin 2 x$

$= \sin 2 x + \sin 2 x - 2 \sin 2 x = 0$ ,

(Vì $\cos \frac{2 π}{3}$ = $\cos \frac{4 π}{3}$ = $- \frac{1}{2}$ .)

Vậy $y^{'} = 0$ với mọi $x$ , do đó $y^{'}$ không phụ thuộc vào $x$ .

Cách khác:

$\begin{array}{l} y = 1 + \frac{1}{2} [\cos (\frac{2 π}{3} - 2 x) + \cos (\frac{4 π}{3} - 2 x)] \\ + \frac{1}{2} [\cos (\frac{2 π}{3} + 2 x) + \cos (\frac{4 π}{3} + 2 x)] + \cos 2 x \\ = 1 + \frac{1}{2} .2 \cos (π - 2 x) \cos \frac{π}{3} \\ + \frac{1}{2} .2 \cos (π + 2 x) \cos \frac{π}{3} + \cos 2 x \\ = 1 - \cos 2 x . \frac{1}{2} - \cos 2 x . \frac{1}{2} + \cos 2 x \\ = 1 - \cos 2 x + \cos 2 x = 1 \\ \Rightarrow y = 1, \forall x \\ \Rightarrow y^{'} = 0, \forall x \end{array}$

Bài 7 trang 168 sgk Đại số và Giải tích 11: Giải phương trình

f^{'} (x) = 0

, biết rằng:

a. $f (x) = 3 \cos x + 4 \sin x + 5 x$

b. $f (x) = 1 - \sin (π + x) + 2 \cos (\frac{2 π + x}{2})$

Phương pháp giải:

Sử dụng bảng đạo hàm cơ bản và các quy tắc tính đạo hàm, tính đạo hàm của hàm số, sau đó giải phương trình lượng giác.

Phương pháp giải phương trình dạng $a \sin x + b \cos x = c$ : Chia cả 2 vế cho $\sqrt{a^{2} + b^{2}}$ .

Lời giải:

$f^{'} (x) = - 3 \sin x + 4 \cos x + 5$ . Do đó

$f^{'} (x) = 0 \Leftrightarrow - 3 \sin x + 4 \cos x + 5 = 0$

$\Leftrightarrow 3 \sin x - 4 \cos x = 5$

$\Leftrightarrow \frac{3}{5} \sin x - \frac{4}{5} c o s x = 1$ . (1)

Đặt $\cos φ = \frac{3}{5}$ , $(φ \in (0; \frac{π}{2})) \Rightarrow \sin φ = \frac{4}{5}$ , ta có:

(1) $\Leftrightarrow \sin x . \cos φ - \cos x . \sin φ = 1 \Leftrightarrow \sin (x - φ) = 1$

$\Leftrightarrow x - φ = \frac{π}{2} + k 2 π \Leftrightarrow x = φ + \frac{π}{2} + k 2 π, k \in Z$

Phương pháp giải:

Sử dụng mối liên hệ của các góc phụ nhau, bù nhau, hơn kém nhau $π$ , hơn kém nhau $\frac{π}{2}$ và giải phương trình lượng giác cơ bản

Lời giải:

$\begin{array}{l} f^{'} (x) = {(1)}^{'} - {[\sin (π + x)]}^{'} + 2 {[\cos (π + \frac{x}{2})]}^{'} \\ = - {(π + x)}^{'} \cos (π + x) + 2 {(π + \frac{x}{2})}^{'} . [- \sin (π + \frac{x}{2})] \\ = - \cos (π + x) + 2. \frac{1}{2} . [- \sin (π + \frac{x}{2})] \end{array}$

$f^{'} (x) = - \cos (π + x) - \sin (π + \frac{x}{2}) = \cos x + \sin \frac{x}{2}$

$f^{'} (x) = 0 \Leftrightarrow \cos x + \sin \frac{x}{2} = 0 \Leftrightarrow \sin \frac{x}{2} = - c o s x$

$\Leftrightarrow s i n \frac{x}{2} = s i n (x - \frac{π}{2})$

$\begin{array}{l} \Leftrightarrow [\begin{array}{l} \frac{x}{2} = x - \frac{π}{2} + k 2 π \\ \frac{x}{2} = π - x + \frac{π}{2} + k 2 π \end{array} \end{array}$

$\Leftrightarrow [\begin{array}{l} - \frac{x}{2} = - \frac{π}{2} + k 2 π \\ \frac{3 x}{2} = \frac{3 π}{2} + k 2 π \end{array}$ $\Leftrightarrow [\begin{array}{l} x = π - k 4 π \\ x = π + \frac{k 4 π}{3} \end{array}$

$\Leftrightarrow x = π + \frac{k 4 π}{3}$

Cách khác:

$\begin{array}{l} f (x) = 1 - \sin (π + x) + 2 \cos (\frac{2 π + x}{2}) \\ = 1 + \sin x + 2 \cos (π + \frac{x}{2}) \\ = 1 + \sin x - 2 \cos \frac{x}{2} \\ f^{'} (x) = {(1 + \sin x - 2 \cos \frac{x}{2})}^{'} \\ = {(1)}^{'} + {(\sin x)}^{'} - 2 {(\cos \frac{x}{2})}^{'} \\ = 0 + \cos x - 2. \frac{1}{2} (- \sin \frac{x}{2}) \\ = \cos x + \sin \frac{x}{2} \\ f^{'} (x) = 0 \Leftrightarrow \cos x + \sin \frac{x}{2} = 0 \\ \Leftrightarrow \cos x = - \sin \frac{x}{2} = - \cos (\frac{π}{2} - \frac{x}{2}) \\ \Leftrightarrow \cos x = \cos (π - (\frac{π}{2} - \frac{x}{2})) \\ \Leftrightarrow \cos x = \cos (\frac{π}{2} + \frac{x}{2}) \\ \Leftrightarrow [\begin{array}{l} x = \frac{π}{2} + \frac{x}{2} + k 2 π \\ x = - \frac{π}{2} - \frac{x}{2} + k 2 π \end{array} \\ \Leftrightarrow [\begin{array}{l} \frac{x}{2} = \frac{π}{2} + k 2 π \\ \frac{3 x}{2} = - \frac{π}{2} + k 2 π \end{array} \\ \Leftrightarrow [\begin{array}{l} x = π + k 4 π \\ x = - \frac{π}{3} + \frac{k 4 π}{3} \end{array} \end{array}$

Chú ý:

Ở họ nghiệm thứ 2 nếu cho $k = 1 + l, l \in Z$ thì:

$x = - \frac{π}{3} + \frac{k 4 π}{3} = - \frac{π}{3} + \frac{(1 + l) 4 π}{3}$

$= - \frac{π}{3} + \frac{4 π + l 4 π}{3} = - \frac{π}{3} + \frac{4 π}{3} + \frac{l 4 π}{3}$

$= π + \frac{l 4 π}{3}$

Do đó hai họ nghiệm $x = π + k 4 π$ và $x = π + \frac{l 4 π}{3}$ hợp lại vẫn được họ nghiệm $x = π + \frac{l 4 π}{3}$ trùng với kết quả cách 1.

Bài 8 trang 168 sgk Đại số và Giải tích 11: Giải bất phương trình

f^{'} (x) > g^{'} (x)

, biết rằng:

a. $f (x) = x^{3} + x - \sqrt{2}$ , $g (x) = 3 x^{2} + x + \sqrt{2}$

b. $f (x) = 2 x^{3} - x^{2} + \sqrt{3}$ , $g (x) = x^{3} + \frac{x^{2}}{2} - \sqrt{3}$

Phương pháp giải:

Tính đạo hàm của các hàm số $f (x), g (x)$ và giải bất phương trình.

Lời giải:

$\begin{array}{l} f^{'} (x) = 3 x^{2} + 1 \\ g^{'} (x) = 6 x + 1 \\ f^{'} (x) > g^{'} (x) \Leftrightarrow 3 x^{2} + 1 > 6 x + 1 \\ \Leftrightarrow 3 x^{2} - 6 x > 0 \Leftrightarrow 3 x (x - 2) > 0 \\ \Leftrightarrow [\begin{array}{l} x > 2 \\ x < 0 \end{array} \\ \Rightarrow x \in (- \infty; 0) \cup (2; + \infty) \end{array}$

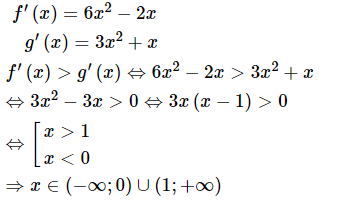
Lý thuyết Bài Đạo hàm của hàm số lượng giác

1. Giới hạn của $\frac{\sin x}{x}$

Ta thừa nhận định lý: $\lim_{x \to 0} \frac{\sin (x)}{x} = 1$

2. Đạo hàm của hàm số lượng giác

+ Hàm số $y = \sin x$ có đạo hàm $\forall x \in R$ và $(\sin x)^{'} = \cos x$ ;

+ Hàm số $y = \cos x$ có đạo hàm $\forall x \in R$ và $(\cos x)^{'} = - \sin x$ ;

+ Hàm số $y = \tan x$ có đạo hàm $\forall x \neq \frac{π}{2} + k π, k \in$ và $(\tan x)^{'} = \frac{1}{\cos^{2} x}$ ;

+ Hàm số $y = \cot x$ có đạo hàm $\forall x \neq k π, k \in$ và $(\cot x)^{'} = - \frac{1}{\sin^{2} x}$

3. Bảng tổng hợp đạo hàm của hàm số lượng giác

$(\sin x)^{'} = \cos x$	$(\sin u)^{'} = (\cos u) . u^{'} = u^{'} . \cos u$
$(\cos x)^{'} = - \sin x$	$(\cos u)^{'} = (- \sin u) . u^{'} = - u^{'} . \sin u$
$(\tan x)^{'} = \frac{1}{\cos^{2} x}$	$(\tan u)^{'} = \frac{u^{'}}{\cos^{2} u}$
$(\cot x)^{'} = - \frac{1}{\sin^{2} x}$	$(\cot u)^{'} = - \frac{u^{'}}{\sin^{2} u}$

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Toán Học Lớp 11

Giải Toán 11 Bài 3: Đạo hàm của hàm số lượng giác

Xem thêm các chương trình khác: