Giải Toán 11 Bài 4: Cấp số nhân

60 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Toán 11 Bài 4: Cấp số nhân chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Cấp số nhân lớp 11.

Giải bài tập Toán 11 Bài 4: Cấp số nhân

Trả lời câu hỏi giữa bài

Trả lời hoạt động 1 trang 98 sgk Đại số và Giải tích 11: Tục truyền rằng nhà vua Ấn Độ cho phép người phát minh ra bàn cờ Vua được lựa chọn một phần thưởng tùy theo sở thích. Người đó chỉ xin nhà vua thưởng cho số thóc bằng số thóc được đặt lên 64 ô của bàn cờ như sau: Đặt lên ô thứ nhất của bàn cờ một hạt thóc, tiếp ô thứ hai hai hạt, … cứ như vậy, số hạt thóc ở ô sau gấp đôi số hạt thóc ở ô trước cho đến ô cuối cùng.

Hãy cho biết số hạt thóc ở các ô từ ô thứ nhất đến thứ sáu của bàn cờ.

Lời giải:

Số hạt thóc ở các ô từ ô thứ nhất đến thứ sáu là: 1; 2; 4; 8; 16; 32

Trả lời hoạt động 2 trang 99 sgk Đại số và Giải tích 11: Hãy đọc hoạt động 1 và cho biết ô thứ 11 có bao nhiêu hạt thóc?

Lời giải:

Từ câu hỏi 1 ta thấy:

Ô thứ 1 có $1 = 2^{0} = 2^{1 - 1}$ hạt thóc.

Ô thứ 2 có $2 = 2^{1} = 2^{2 - 1}$ hạt thóc.

Ô thứ 3 có $4 = 2^{2} = 2^{3 - 1}$ hạt thóc.

Ô thứ 4 có $8 = 2^{3} = 2^{4 - 1}$ hạt thóc.

Ô thứ 5 có $16 = 2^{4} = 2^{5 - 1}$ hạt thóc.

...

Tổng quát: Ô thứ n có $2^{n - 1}$ hạt thóc.

Ô thứ 11 có: $2^{11 - 1} = 2^{10} = 1024$ hạt thóc

Trả lời hoạt động 3 trang 101 sgk Đại số và Giải tích 11: Cho cấp số nhân (u_n) với u₁ = -2 và q =

\frac{- 1}{2}

a. Viết năm số hạng đầu của nó

b. So sánh

u_{2}^{2}

với tích

u_{1} . u_{3}

và

u_{3}^{2}

với tích

u_{2} . u_{4}

. Nêu nhận xét tổng quát từ kết quả trên

Lời giải:

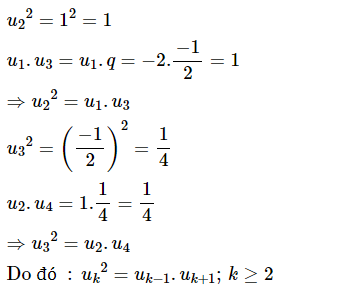
Trả lời hoạt động 4 trang 101 sgk Đại số và Giải tích 11: Tính tổng số các hạt thóc ở 11 ô đầu của bàn cờ nêu ở hoạt động 1Phương pháp giải: Nhân cả tổng S cần tính với 2 rồi lấy 2S-S, thu gọn ta được kết quả.

Lời giải:

Ta có:

$\begin{array}{l} u_{1} = 1 \\ u_{2} = 2 \\ u_{3} = 2^{2} \\ . . . \\ u_{11} = 2^{10} \end{array}$

$\Rightarrow S = u_{1} + u_{2} + . . . + u_{10}$ $= 1 + 2 + 2^{2} + . . . + 2^{10}$

$\Rightarrow 2 S = 2 + 2^{2} + . . . + 2^{10} + 2^{11}$

$\Rightarrow 2 S - S = (2 + 2^{2} + . . . + 2^{10} + 2^{11})$ $- (1 + 2 + 2^{2} + . . . + 2^{10})$

$\Rightarrow S = 2^{11} - 1 = 2047$

Cách tổng quát:

Ta có:

$\begin{array}{l} S = u_{1} + u_{2} + u_{3} + u_{4} + u_{5} + u_{6} + u_{7} + u_{8} + u_{9} + u_{10} + u_{11} \\ = u_{1} + u_{1} . q + u_{1} . q^{2} + \dots + u_{1} . q^{9} + u_{1} . q^{10} (1) \\ \Rightarrow S . q = u_{1} . q + u_{1} . q^{2} + \dots + u_{1} . q^{9} + u_{1} . q^{10} + u_{1} . q^{11} (2) \end{array}$

Lấy (1) trừ (2), ta được:

$(1 - q) S = u_{1} (1 - q^{11})$

$\Rightarrow S = \frac{u_{1} (1 - q^{11})}{1 - q}$

Do đó tổng số hạt thóc của 11 ô đầu là $S = \frac{1 (1 - 2^{11})}{1 - 2} = 2^{11} - 1 = 2047$

Trả lời hoạt động 5 trang 102 sgk Đại số và Giải tích 11: Tính tổng:

$S = 1 + \frac{1}{3} + \frac{1}{3^{2}} + . . . + \frac{1}{3^{n}}$

Phương pháp giải:

Sử dụng công thức tính tổng cấp số nhân:

$S_{n} = \frac{u_{1} (1 - q^{n})}{1 - q}$

Lời giải:

Cấp số nhân có: $u_{1} = 1$ , $q = \frac{1}{3}$

S là tổng của $n + 1$ số hạng đầu tiên

$\Rightarrow S = \frac{u_{1} (1 - q^{n + 1})}{1 - q} = \frac{1. [1 - {(\frac{1}{3})}^{n + 1}]}{1 - \frac{1}{3}}$ $= \frac{3}{2} [1 - {(\frac{1}{3})}^{n + 1}]$

Cách 2:

Ta có:

$\begin{array}{l} S = 1 + \frac{1}{3} + \frac{1}{3^{2}} + \frac{1}{3^{3}} + . . . + \frac{1}{3^{n}} \\ \Rightarrow 3 S = 3 + 1 + \frac{1}{3} + \frac{1}{3^{2}} + . . . + \frac{1}{3^{n - 1}} \\ \Rightarrow 3 S = 3 + S - \frac{1}{3^{n}} \\ \Rightarrow 2 S = 3 - \frac{1}{3^{n}} \\ \Rightarrow S = \frac{1}{2} (3 - \frac{1}{3^{n}}) = \frac{3}{2} (1 - \frac{1}{3^{n + 1}}) \end{array}$

Bài tập (trang 103, 104 sgk Đại số và Giải tích 11)

Bài 1 trang 103 sgk Đại số và Giải tích 11: Chứng minh các dãy số

(\frac{3}{5} . 2^{n}), (\frac{5}{2^{n}}), {(\frac{- 1}{2})}^{n}

là các cấp số nhân.

Phương pháp giải: Chứng minh

\frac{u_{n} + 1}{u_{n}}

là một số không đổi.

Lời giải:

+) Ta có: $u_{n} = \frac{3}{5} {.2}^{n} \Rightarrow u_{1} = \frac{3}{5} {.2}^{1} = \frac{6}{5}$

Với mọi $\forall n \in N^{*}$ , ta có:

$u_{n + 1} = \frac{3}{5} {.2}^{n + 1}$ $\Rightarrow \frac{u_{n + 1}}{u_{n}} = \frac{\frac{3}{5} {.2}^{n + 1}}{\frac{3}{5} {.2}^{n}}$ $= \frac{2^{n + 1}}{2^{n}} = \frac{2^{n} .2}{2^{n}} = 2$ (không đổi)

Vậy dãy số đã cho là một cấp số nhân với $u_{1} = \frac{6}{5}$ và $q = 2$ .

+) Ta có: $u_{n} = \frac{5}{2^{n}} \Rightarrow u_{1} = \frac{5}{2^{1}} = \frac{5}{2}$

Với mọi $\forall n \in N^{*}$ , ta có:

$\frac{u_{n + 1}}{u_{n}} = \frac{\frac{5}{2^{n + 1}}}{\frac{5}{2^{n}}} = \frac{5}{2^{n + 1}} : \frac{5}{2^{n}}$ $= \frac{5}{2^{n + 1}} . \frac{2^{n}}{5} = \frac{2^{n}}{2^{n + 1}} = \frac{2^{n}}{2^{n} .2} = \frac{1}{2}$ (không đổi)

Vậy dãy số đã cho là một cấp số nhân với $u_{1} = \frac{5}{2}$ và $q = \frac{1}{2}$

+) Ta có: $u_{n} = {(- \frac{1}{2})}^{n} \Rightarrow u_{1} = {(- \frac{1}{2})}^{1} = - \frac{1}{2}$

Với mọi $\forall n \in N^{*}$ , ta có:

$\frac{u_{n + 1}}{u_{n}} = \frac{{(- \frac{1}{2})}^{n + 1}}{{(- \frac{1}{2})}^{n}} = \frac{{(- \frac{1}{2})}^{n} . (- \frac{1}{2})}{{(- \frac{1}{2})}^{n}} = - \frac{1}{2}$ (không đổi)

Vậy dãy số đã cho là cấp số nhân với $u_{1} = \frac{- 1}{2}$ và $q = \frac{- 1}{2}$ .

Bài 2 trang 103 sgk Đại số và Giải tích 11: Cho cấp số nhân với công bội q

a. Biết u₁ = 2, u₆ = 486. Tìm q

b. Biết q =

\frac{2}{3}

, u₄ =

\frac{8}{21}

.Tìm u₁
c. Biết u₁ = 3, q = -2. Hỏi số 192 là số hạng thứ mấy?

Phương pháp giải: Sử dụng công thức số hạng tổng quát của cấp số nhân: u_n = u¹.q^n-1

Lời giải:

Bài 3 trang 103 sgk Đại số và Giải tích 11: Tìm các số hạng của cấp số nhân (u_n) có năm số hạng, biết:
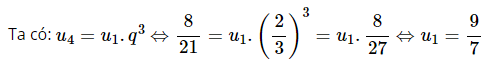
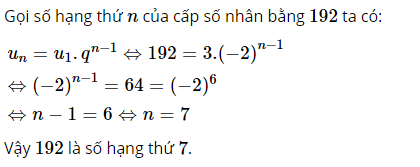
a. u₃=3 và u₅=27

b. u₄-u₂=25 và u₃-u₁=50

Phương pháp giải:

Sử dụng công thức số hạng tổng quát của cấp số nhân: u_n=u₁.q^n-1.

Lời giải:

a. Trong cấp số nhân, ta có:

u_{n} = u_{1} . q^{n - 1}

Trong đó

u_{1}

là số hạng thứ nhất,

u_{n}

là số hạng thứ n và q là công bội.

Mà:

$\begin{array}{l} {\begin{cases} u_{3} = 3 \\ u_{5} = 27 \end{cases} \Leftrightarrow {\begin{cases} u_{1} . q^{2} = 3 \\ u_{1} . q^{4} = 27 \end{cases} \\ \Rightarrow \frac{u_{1} . q^{4}}{u_{1} . q^{2}} = \frac{27}{3} \Leftrightarrow q^{2} = 9 \Leftrightarrow q = \pm 3 \\ +) q = 3 \Rightarrow u_{1} {.3}^{2} = 3 \\ \Leftrightarrow u_{1} = \frac{3}{3^{2}} = \frac{1}{3} \\ \Rightarrow C S N : \frac{1}{3}; 1; 3; 9; 27 \\ +) q = - 3 \Rightarrow u_{1} . {(- 3)}^{2} = 3 \\ \Leftrightarrow u_{1} = \frac{3}{{(- 3)}^{2}} = \frac{1}{3} \\ \Rightarrow C S N : \frac{1}{3}; - 1; 3; - 9; 27 \end{array}$

b. Ta có: $u_{4} = u_{1} q^{3}; u_{2} = u_{1} q; u_{3} = u_{1} q^{2}$

Theo bài ra:

$\begin{array}{l} {\begin{cases} u_{4} - u_{2} = 25 \\ u_{3} - u_{1} = 50 \end{cases} \\ \Leftrightarrow {\begin{cases} u_{1} q^{3} - u_{1} q = 25 \\ u_{1} q^{2} - u_{1} = 50 \end{cases} \\ \Leftrightarrow {\begin{cases} u_{1} q (q^{2} - 1) = 25 \\ u_{1} (q^{2} - 1) = 50 \end{cases} \\ \Rightarrow \frac{u_{1} q (q^{2} - 1)}{u_{1} (q^{2} - 1)} = \frac{25}{50} \Leftrightarrow q = \frac{25}{50} = \frac{1}{2} \\ \Rightarrow u_{1} . {(\frac{1}{2})}^{2} - u_{1} = 50 \\ \Leftrightarrow u_{1} . (- \frac{3}{4}) = 50 \Leftrightarrow u_{1} = \frac{- 200}{3} \\ \Rightarrow C S N : \frac{- 200}{3}; \frac{- 100}{3}; \frac{- 50}{3}; \frac{- 25}{3}; \frac{- 25}{6} \end{array}$

Bài 4 trang 104 sgk Đại số và Giải tích 11: Tìm cấp số nhân có sáu số hạng, biết rằng tổng của năm số hạng đầu là 31 và tổng của năm số hạng sau là 62.

Phương pháp giải:

Sử dụng công thức số hạng tổng quát của CSN: u_n=u₁q^n-1 và công thức tổng n số hạng đầu tiên của CSN:

S_{n} = \frac{u_{1} (1 - q^{n})}{1 - q}

Lời giải:

Giả sử có cấp số nhân: $u_{1}, u_{2}, u_{3}, u_{4}, u_{5}, u_{6}$

Theo giả thiết ta có:

$u_{1} + u_{2} + u_{3} + u_{4} + u_{5} = 31$ . (1)

$u_{2} + u_{3} + u_{4} + u_{5} + u_{6} = 62$ . (2)

Nhân hai vế của (1) với $q$ , ta được: $u_{1} q + u_{2} q + u_{3} q + u_{4} q + u_{5} q = 31 q$

$\Leftrightarrow$ $u_{2} + u_{3} + u_{4} + u_{5} + u_{6} = 31 q$ (3)

Từ (2) và (3) $\Rightarrow 62 = 31. q \Rightarrow q = 2$ .

Ta có $S_{5} = 31 \Leftrightarrow \frac{u_{1} (1 - 2^{5})}{1 - 2} = 31$ $\Leftrightarrow 31 u_{1} = 31 \Leftrightarrow u_{1} = 1$

Vậy ta có cấp số nhân là: $1, 2, 4, 8, 16, 32$ .

Cách khác:

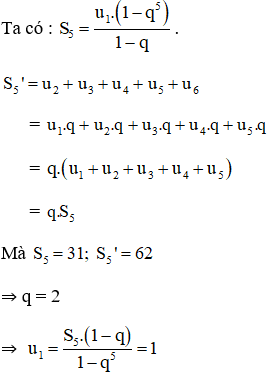
Vậy ta có cấp số nhân là: $1, 2, 4, 8, 16, 32$ .

Bài 5 trang 104 sgk Đại số và Giải tích 11: Tỉ lệ tăng dân số của tỉnh X là 1,4%. Biết rằng số dân của tỉnh hiện nay là 1,8 triệu người. Hỏi với mức tăng như vậy thì sau 5 năm, 10 năm số dân của tỉnh đó là bao nhiêu?

Phương pháp giải:

Số dân của tỉnh đó sau mỗi năm lập thành cấp số nhân, với $u_{1} = 1, 8, q = 1 + 1, 4 % = 1, 014$ .

Sử dụng công thức tìm số hạng tổng quát của cấp số nhân: $u_{n} = u_{1} . q^{n - 1}$

Lời giải:

Giả sử số dân của một tỉnh đó hiện nay là $N$ . Vì tỉ lệ tăng dân số là $1, 4 %$ nên sau một năm, số dân tăng thêm là $1, 4 % . N$ .

Vậy số dân của tỉnh đó vào năm sau là

$N + 1, 4 % . N = 101, 4 % . N$ $= \frac{101, 4}{100} . N$ .

Như vậy số dân của tỉnh đó sau mỗi năm lập thành cấp số nhân.

Hiện tại: $u_{1} = N$

Sau 1 năm: $u_{2} = \frac{101, 4}{100} . N$

Sau 2 năm: $u_{3} = (\frac{101, 4}{100})^{2} . N$ ;...

Vậy nếu $N = 1, 8$ triệu người

Áp dụng công thức tính số hạng tổng quát của cấp số nhân thì:

Sau $5$ năm số dân của tỉnh là $u_{6} = (\frac{101, 4}{100})^{5} .1, 8 \approx 1, 9$ (triệu người)

Sau $10$ năm số dân của tỉnh là $u_{11} = (\frac{101, 4}{100})^{10} .1, 8 \approx 2, 1$ (triệu người).

Bài 6 trang 104 sgk Đại số và Giải tích 11: Cho hình vuông C1 có cạnh bằng 4. Người ta chia mỗi cạnh của hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông C2 (hình bên). Từ hình vuông C2 lại tiếp tục như trên để được hình vuông C3… Tiếp tục quá trình trên, ta nhận được các dãy các hình vuông C1, C2, C3, …,Cn

Gọi an là độ dài cạnh của hình vuông Cn. Chứng minh dãy số (an) là một cấp số nhân

Lời giải:

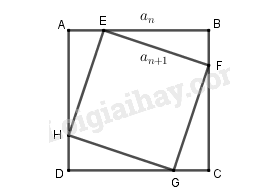
Xét dãy số $(a_{n})$ , ta có $a_{1} = 4$ .

Gọi $a_{n}$ là cạnh hình vuông $C_{n}$ .

Ta tính cạnh hình vuông $a_{n + 1}$ như sau:

Xét tam giác $B E F$ vuông tại $B$ có $B E = \frac{3}{4} B A = \frac{3 a_{n}}{4}$ , $B F = \frac{1}{4} B C = \frac{a_{n}}{4}$

Do đó $E F = \sqrt{B E^{2} + B F^{2}}$ $= \sqrt{{(\frac{3 a_{n}}{4})}^{2} + {(\frac{a_{n}}{4})}^{2}} = \frac{\sqrt{10}}{4} a_{n}$ hay $a_{n + 1} = \frac{\sqrt{10}}{4} a_{n}$ .

Vậy dãy số $(a_{n})$ là cấp số nhân với số hạng đầu là $a_{1} = 4$ và công bội $q = \frac{\sqrt{10}}{4}$

Lý thuyết Bài Cấp số nhân

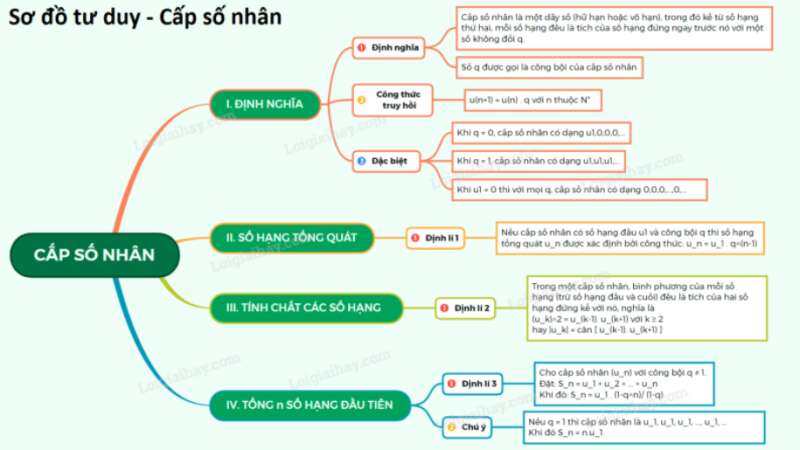
1. Định nghĩa

$u_{n}$ là cấp số nhân $\Leftrightarrow u_{n + 1} = u_{n} . q$ , với $n \in N^{*}$

Công bội $q = \frac{u_{n + 1}}{u_{n}}$ .

Ví dụ:

Cho cấp số nhân $(u_{n})$ thỏa mãn $u_{1} = 5, q = 3$ . Tính $u_{2}$ .

Ta có: $u_{2} = q u_{1} = 3.5 = 15$ .

2. Số hạng tổng quát

$u_{n} = u_{1} . q^{n - 1}, (n \geq 2)$

Ví dụ:

Cho cấp số nhân $(u_{n})$ thỏa mãn $u_{1} = 5, q = 3$ . Tính $u_{5}$ .

Ta có:

$u_{5} = u_{1} q^{4} = {5.3}^{4} = 405$ .

3. Tính chất

$u_{k}^{2} = u_{k - 1} . u_{k + 1}$ hay $| u_{k} | = \sqrt{u_{k - 1} . u_{k + 1}},$ với $k \geq 2$

Ví dụ:

Cho bốn số $x; 5; 25; y$ theo thứ tự đó lập thành một CSN. Tìm $x, y$ .

Ta có:

$\begin{array}{l} 5^{2} = x .25 \Leftrightarrow x = 1 \\ 25^{2} = 5 y \Leftrightarrow y = 125 \end{array}$

Vậy $x = 1, y = 125$ .

4. Tổng n số hạng đầu

$S_{n} = \frac{u_{1} (q^{n} - 1)}{q - 1}$ $= \frac{u_{1} (1 - q^{n})}{1 - q}$ , $(q \neq 1)$ .

Ví dụ:

Cho cấp số nhân $(u_{n})$ thỏa mãn $u_{1} = 5, q = 3$ . Tính $S_{10}$ .

Ta có:

$\begin{array}{l} S_{10} = \frac{u_{1} (1 - q^{10})}{1 - q} \\ = \frac{5. (1 - 3^{10})}{1 - 3} \\ = \frac{5 (3^{10} - 1)}{2} \end{array}$

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Toán Học Lớp 11

Giải Toán 11 Bài 4: Cấp số nhân

Xem thêm các chương trình khác: