Giải Toán 11 Bài 3: Một số phương trình lượng giác thường gặp

63 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Toán 11 Bài 3: Một số phương trình lượng giác thường gặp chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Một số phương trình lượng giác thường gặp lớp 11.

Giải bài tập Toán 11 Bài 3: Một số phương trình lượng giác thường gặp

Trả lời câu hỏi giữa bài

Trả lời hoạt động 1 trang 29 sgk Đại số và Giải tích 11: Giải các phương trình trong ví dụ 1.

2 s i n x - 3 = 0

là phương trình bậc nhất đối với sinx.

\sqrt{3} \tan x + 1 = 0

là phương trình bậc nhất đối với

\tan x

Phương pháp giải:

Chuyển vế đưa về PT lượng giác cơ bản

s i n x = a

Lời giải:

2 s i n x - 3 = 0 \Leftrightarrow s i n x = \frac{3}{2}

, vô nghiệm vì

s i n x \leq 1 < \frac{3}{2}

với mọi x.

Phương pháp giải:

B1: đưa PT về dạng $\tan x = a$

B2: tìm $α$ sao cho $\tan α = a \Rightarrow$ PT trở về dạng $\tan x = \tan α$

B3: Kết luận nghiệm

Lời giải:

$\sqrt{3} \tan x + 1 = 0 \Leftrightarrow t a n x = \frac{- \sqrt{3}}{3} \Leftrightarrow t a n x = \tan \frac{- π}{6}$

$\Leftrightarrow x = \frac{- π}{6} + k π, k \in Z$

Trả lời hoạt động 2 trang 31 sgk Đại số và Giải tích 11: Giải các phương trình sau:

Phương pháp giải:

B1: Đặt ẩn phụ $t = \cos x$ đưa về giải PT bậc hai ẩn $t$

B2: Sau khi tìm được $t$ , bài toán đưa về giải PT lượng giác cơ bản.

B3. Giải và KL nghiệm $x$ .

Lời giải:

$3 \cos^{2} x - 5 \cos x + 2 = 0$

Đặt $\cos x = t$ với điều kiện $- 1 \leq t \leq 1$ (*),

ta được phương trình bậc hai theo t:

$\begin{array}{l} 3 t^{2} - 5 t + 2 = 0 (1) \\ Δ = {(- 5)}^{2} - 4.3.2 = 1 \end{array}$

Phương trình (1) có hai nghiệm là:

$\begin{aligned} t_{1} = \frac{- (- 5) + \sqrt{1}}{2.3} = \frac{6}{6} = 1 (thỏa mãn) \\ t_{2} = \frac{- (- 5) - \sqrt{1}}{2.3} = \frac{4}{6} = \frac{2}{3} (thỏa mãn) \end{aligned}$

Ta có:

$\begin{array}{l} \cos x = 1 \Leftrightarrow \cos x = \cos 0 \\ \Leftrightarrow x = k 2 π, k \in Z \end{array}$

$\cos x = \frac{2}{3} \Leftrightarrow x = \pm a r c c o s \frac{2}{3} + k 2 π, k \in Z$

Phương pháp giải:

B1: Đặt ẩn phụ $t = \tan x$ đưa về giải PT bậc hai ẩn $t$

B2: Sau khi tìm được $t$ , bài toán đưa về giải PT lượng giác cơ bản.

B3. Giải và KL nghiệm $x$ .

Lời giải:

$3 \tan^{2} x - 2 \sqrt{3} t a n x + 3 = 0$

Đặt $t = \tan x$

Ta được phương trình bậc hai theo $t$ :

$\begin{array}{l} 3 t^{2} - 2 \sqrt{3} t + 3 = 0 (1) \\ Δ = {(- 2 \sqrt{3})}^{2} - 4.3.3 = - 24 < 0 \end{array}$

Vậy phương trình (1) vô nghiệm, không có $x$ thỏa mãn đề bài

Trả lời hoạt động 3 trang 32 sgk Đại số và Giải tích 11: Hãy nhắc lại:

a. Các hằng đẳng thức lượng giác cơ bản

b. Công thức cộng

c. Công thức nhân đôi

d. Công thức biến đổi tích thành tổng và tổng thành tích

Lời giải:

Các hằng đẳng thức lượng giác cơ bản:

$\sin^{2} α + \cos^{2} a = 1$

$1 + \tan^{2} α = \frac{1}{\cos^{2} α}$ ; $α \neq \frac{π}{2} + k π, k \in Z$

$1 + c o t^{2} α = \frac{1}{\sin^{2} α}; α \neq k π, k \in Z$

$t a n α . c o t α = 1; α \neq \frac{k π}{2}, k \in Z$

Công thức cộng:

$c o s (a - b) = c o s a c o s b + s i n a s i n b c o s (a + b) = c o s a c o s b - s i n a s i n b s i n (a - b) = s i n a c o s b - c o s a s i n b$

$\begin{aligned} \tan (a - b) = \frac{\tan a - \tan b}{1 + \tan a . \tan b} \\ \tan (a + b) = \frac{\tan a + \tan b}{1 - \tan a . \tan b} \end{aligned}$

Công thức nhân đôi:

$s i n 2 α = 2 s i n α c o s α c o s 2 α = c o s^{2} α - s i n^{2} α = 2 c o s^{2} a - 1 = 1 - 2 s i n^{2} a$

$\tan 2 α = \frac{2 \tan α}{1 - \tan^{2} α}$

Công thức biến đổi tích thành tổng:

$c o s a c o s b = \frac{1}{2} [c o s (a - b) + c o s (a + b)]$

$s i n a s i n b = \frac{1}{2} [c o s (a - b) - c o s (a + b)]$

$s i n a c o s b = \frac{1}{2} [s i n (a - b) + s i n (a + b)]$

Công thức biến đổi tổng thành tích:

$\begin{aligned} \cos u + \cos v = 2 \cos \frac{u + v}{2} \cos \frac{u - v}{2} \\ \cos u - \cos v = - 2 \sin \frac{u + v}{2} \sin \frac{u - v}{2} \\ \sin u + \sin v = 2 \sin \frac{u + v}{2} \cos \frac{u - v}{2} \\ \sin u - \sin v = 2 \cos \frac{u + v}{2} \sin \frac{u - v}{2} \end{aligned}$

Trả lời hoạt động 4 trang 34 sgk Đại số và Giải tích 11: Giải phương trình 3cos² 6x + 8sin3x cos3x – 4 = 0

Phương pháp giải:

- Biến đổi phương trình về bậc hai với ẩn $t = \sin 6 x$ .

- Giải phương trình ẩn $t$ và suy ra nghiệm.

Lời giải:

$3 c o s^{2} 6 x + 8 s i n 3 x c o s 3 x - 4 = 0 \Leftrightarrow 3 (1 - s i n^{2} 6 x) + 4 s i n 6 x - 4 = 0 \Leftrightarrow - 3 s i n^{2} 6 x + 4 s i n 6 x - 1 = 0$

Đặt $s i n 6 x = t$ với điều kiện $- 1 \leq t \leq 1$ (*), ta được phương trình bậc hai theo t:

-3t² + 4t - 1 = 0(1)

Δ = 4² - 4.(-1).(-3) = 4

Phương trình (1) có hai nghiệm là:

$\begin{aligned} t_{1} = \frac{- 4 + \sqrt{4}}{2. (- 3)} = \frac{1}{3} (T M) \\ t_{2} = \frac{- 4 - \sqrt{4}}{2. (- 3)} = 1 (T M) \end{aligned}$

Ta có:

$s i n 6 x = \frac{1}{3} \Leftrightarrow 6 x = a r c s i n \frac{1}{3} + k 2 π$ và $6 x = π - a r c s i n \frac{1}{3} + k 2 π \Leftrightarrow x = \frac{1}{6} a r c s i n \frac{1}{3} + \frac{k π}{3}$ và $x = \frac{π}{6} - \frac{1}{6} a r c s i n \frac{1}{3} + \frac{k π}{3}, k \in Z$

$s i n 6 x = 1 \Leftrightarrow s i n 6 x = \sin \frac{π}{2}$

$\Leftrightarrow 6 x = \frac{π}{2} + k 2 π, k \in Z$

$\Leftrightarrow x = \frac{π}{12} + \frac{k π}{3}, k \in Z$

Trả lời hoạt động 5 trang 35 sgk Đại số và Giải tích 11: Dựa vào các công thức cộng đã học

$s i n (a + b) = s i n a c o s b + s i n b c o s a; s i n (a - b) = s i n a c o s b - s i n b c o s a; c o s (a + b) = c o s a c o s b - s i n a s i n b; c o s (a - b) = c o s a c o s b + s i n a s i n b$

và kết quả $c o s \frac{π}{4} = s i n \frac{π}{4} = \frac{\sqrt{2}}{2}$ , hãy chứng minh rằng:

s i n x + c o s x = \sqrt{2} c o s (x - \frac{π}{4}

)

s i n x - c o s x = \sqrt{2} s i n (x - \frac{π}{4}

)

Lời giải:

a. $s i n x + c o s x = \sqrt{2} . (\frac{\sqrt{2}}{2} s i n x + \frac{\sqrt{2}}{2} c o s x)$

$= \sqrt{2} . (s i n \frac{π}{4} s i n x + c o s \frac{π}{4} c o s x)$

$= \sqrt{2} . c o s (x - \frac{π}{4})$

Cách khác:

$\sqrt{2} c o s (x - \frac{π}{4}) = \sqrt{2} . (c o s x . c o s \frac{π}{4} + s i n x . s i n \frac{π}{4})$

$= \sqrt{2} . (\frac{\sqrt{2}}{2} . c o s x + \frac{\sqrt{2}}{2} . s i n x) = \sqrt{2} . \frac{\sqrt{2}}{2} . c o s x + \sqrt{2} . \frac{\sqrt{2}}{2} . s i n x = c o s x + s i n x$ (đpcm)

b. $s i n x - c o s x = \sqrt{2} . (\frac{\sqrt{2}}{2} s i n x - \frac{\sqrt{2}}{2} c o s x)$

$= \sqrt{2} . (c o s \frac{π}{4} s i n x - s i n \frac{π}{4} c o s x)$

$= \sqrt{2} . s i n (x - \frac{π}{4}$ )

Cách khác:

$\sqrt{2} . s i n (x - \frac{π}{4}) = \sqrt{2} . (s i n x . c o s \frac{π}{4} - s i n \frac{π}{4} . c o s x) = \sqrt{2} . (\frac{\sqrt{2}}{2} . s i n x - \frac{\sqrt{2}}{2} . c o s x) = \sqrt{2} . \frac{\sqrt{2}}{2} . s i n x - \sqrt{2} . \frac{\sqrt{2}}{2} . c o s x = s i n x - c o s x$ (đpcm).

Trả lời hoạt động 6 trang 36 sgk Đại số và Giải tích 11: Giải phương trình

\sqrt{3} s i n 3 x - c o s 3 x = \sqrt{2}

Phương pháp giải:

Chia cả hai vế cho

2

và sử dụng công thức

\sin (a - b) = \sin a \cos b - \sin b \cos a

biến đổi phương trình.

Lời giải:

Bài tập (trang 36, 37 sgk Đại số và Giải tích 11)

Bài 1 trang 36 sgk Đại số và Giải tích 11: Giải phương trình

$\sin^{2} x - sinx = 0$ .

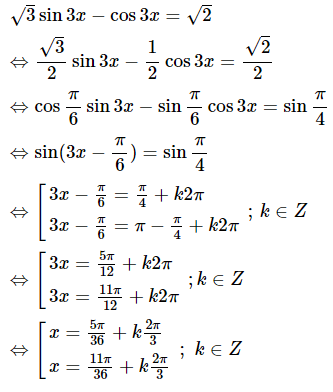
Phương pháp giải:

Đặt nhân tử chung, đưa phương trình về dạng tích và giải các phương trình lượng giác cơ bản:

$\sin x = \sin α \Leftrightarrow [\begin{array}{l} x = α + k 2 π \\ x = π - α + k 2 π \end{array} (k \in Z)$

Lời giải:

$\begin{array}{l} \sin^{2} x - \sin x = 0 \\ \Leftrightarrow \sin x (\sin x - 1) = 0 \\ \Leftrightarrow [\begin{array}{l} \sin x = 0 \\ \sin x - 1 = 0 \end{array} \\ \Leftrightarrow [\begin{array}{l} \sin x = 0 \\ \sin x = 1 \end{array} \\ \Leftrightarrow [\begin{array}{l} x = k π \\ x = \frac{π}{2} + k 2 π \end{array} (k \in Z) \end{array}$

Vậy nghiệm của phương trình là $x = k π$ hoặc $x = \frac{π}{2} + k 2 π (k \in Z)$

Bài 2 trang 36 sgk Đại số và Giải tích 11: Giải các phương trình sau:

a. 2cos2x−3cosx+1=0
b. 2sin2x+√2sin4x=0

Phương pháp giải:

Đặt

t = c o s x

, đưa về phương trình bậc hai ẩn t, giải phương trình bậc hai ẩn t sau đó giải các phương trình lượng giác cơ bản của cos.

Lời giải:

Đặt $t = c o s x, t \in [- 1; 1]$ ta được phương trình:

$\begin{array}{l} 2 t^{2} - 3 t + 1 = 0 \Leftrightarrow [\begin{array}{l} t = 1 (t m) \\ t = \frac{1}{2} (t m) \end{array} \\ +) t = 1 \Leftrightarrow \cos x = 1 \Leftrightarrow x = k 2 π (k \in Z) \\ +) t = \frac{1}{2} \Leftrightarrow \cos x = \frac{1}{2} \Leftrightarrow x = \pm \frac{π}{3} + k 2 π (k \in Z) \end{array}$

Vậy $x = k 2 π$ hoặc $x = \pm \frac{π}{3} + k 2 π$ $(k \in Z)$ .

Phương pháp giải:

+) Sử dụng công thức nhân đôi $\sin 4 x = 2 \sin 2 x \cos 2 x$

+) Đặt nhân tử chung, đưa phương trình về dạng tích.

+) Giải các phương trình lượng giác cơ bản của sin và cos.

Lời giải:

$\begin{array}{l} 2 \sin 2 x + \sqrt{2} \sin 4 x = 0 \\ \Leftrightarrow 2 \sin 2 x + 2 \sqrt{2} \sin 2 x \cos 2 x = 0 \\ \Leftrightarrow 2 \sin 2 x (1 + \sqrt{2} \cos 2 x) = 0 \\ \Leftrightarrow [\begin{array}{l} \sin 2 x = 0 \\ 1 + \sqrt{2} \cos 2 x = 0 \end{array} \\ \Leftrightarrow [\begin{array}{l} \sin 2 x = 0 \\ \cos 2 x = - \frac{1}{\sqrt{2}} \end{array} \\ \Leftrightarrow [\begin{array}{l} 2 x = k π \\ 2 x = \pm \frac{3 π}{4} + k 2 π \end{array} \\ \Leftrightarrow [\begin{array}{l} x = \frac{k π}{2} \\ x = \pm \frac{3 π}{8} + k π \end{array} (k \in Z) \end{array}$

Vậy nghiệm của phương trình là $x = \frac{k π}{2}$ hoặc $x = \pm \frac{3 π}{8} + k π (k \in Z)$ .

Bài 3 trang 37 sgk Đại số và Giải tích 11: Giải các phương trình sau:

Phương pháp giải:

+) Sử dụng công thức $\sin^{2} \frac{x}{2} = 1 - \cos^{2} \frac{x}{2}$

+) Đặt ẩn phụ $t = \cos \frac{x}{2} (t \in [- 1; 1])$ , đưa về phương trình bậc hai ẩn t, giải phương trình suy ra các nghiệm t.

+) Giải các phương trình lượng giác cơ bản của cos: $\cos x = \cos α \Leftrightarrow x = \pm α + k 2 π (k \in Z)$

Lời giải:

$\begin{array}{l} \sin^{2} \frac{x}{2} - 2 \cos \frac{x}{2} + 2 = 0 \\ \Leftrightarrow 1 - \cos^{2} \frac{x}{2} - 2 \cos \frac{x}{2} + 2 = 0 \\ \Leftrightarrow \cos^{2} \frac{x}{2} + 2 \cos \frac{x}{2} - 3 = 0 \end{array}$

Đặt $t = c o s \frac{x}{2}, t \in [- 1; 1]$ thì phương trình trở thành

$\begin{array}{l} t^{2} + 2 t - 3 = 0 \Leftrightarrow [\begin{array}{l} t = 1 (t m) \\ t = - 3 (k t m) \end{array} \\ K h i t = 1 \Leftrightarrow \cos \frac{x}{2} = 1 \Leftrightarrow \frac{x}{2} = k 2 π \\ \Leftrightarrow x = k 4 π (k \in Z) \end{array}$

Vậy nghiệm của phương trình là: $x = k 4 π (k \in Z)$ .

Phương pháp giải:

+) Sử dụng công thức $\cos^{2} x = 1 - \sin^{2} x$

+) Đặt ẩn phụ $t = \sin x (t \in [- 1; 1])$ , đưa về phương trình bậc hai ẩn t, giải phương trình suy ra các nghiệm t.

+) Giải các phương trình lượng giác cơ bản của sin: $\sin x = \sin α \Leftrightarrow [\begin{array}{l} x = α + k 2 π \\ x = π - α + k 2 π \end{array} (k \in Z)$

Lời giải:

$\begin{array}{l} 8 \cos^{2} x + 2 \sin x - 7 = 0 \\ \Leftrightarrow 8 (1 - \sin^{2} x) + 2 \sin x - 7 = 0 \\ \Leftrightarrow 8 \sin^{2} x - 2 \sin x - 1 = 0 \end{array}$

Đặt $t = s i n x, t \in [- 1; 1]$ thì phương trình trở thành

$\begin{array}{l} 8 t^{2} - 2 t - 1 = 0 \Leftrightarrow [\begin{array}{l} t = \frac{1}{2} \\ t = - \frac{1}{4} \end{array} (t m) \\ +) t = \frac{1}{2} \Leftrightarrow \sin x = \frac{1}{2} \\ \Leftrightarrow [\begin{array}{l} x = \frac{π}{6} + k 2 π \\ x = \frac{5 π}{6} + k 2 π \end{array} (k \in Z) \\ +) t = - \frac{1}{4} \Leftrightarrow \sin x = - \frac{1}{4} \\ \Leftrightarrow [\begin{array}{l} x = \arcsin (- \frac{1}{4}) + k 2 π \\ x = π - \arcsin (- \frac{1}{4}) + k 2 π \end{array} (k \in Z) \end{array}$

Phương pháp giải:

+) Tìm ĐKXĐ

+) Đặt ẩn phụ $t = t a n x$ , đưa về phương trình bậc hai ẩn t, giải phương trình suy ra các nghiệm t.

+) Giải phương trình lượng giác cơ bản của tan: $\tan x = \tan α \Leftrightarrow x = α + k π (k \in Z)$

Lời giải:

ĐK: $\cos x \neq 0 \Leftrightarrow x \neq \frac{π}{2} + k π (k \in Z)$

Đặt $t = t a n x$ thì phương trình trở thành

$2 t^{2} + 3 t + 1 = 0 \Leftrightarrow [\begin{matrix} t = - 1 \\ t = - \frac{1}{2} \end{matrix}$

$\Leftrightarrow [\begin{matrix} \tan x = - 1 \\ \tan x = - \frac{1}{2} \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = - \frac{π}{4} + k π \\ x = \arctan (- \frac{1}{2}) + k π \end{matrix} (k \in Z) (t m)$

Phương pháp giải:

+) Tìm ĐKXĐ

+) Sử dụng công thức $\cot x = \frac{1}{\tan x}$ .

+) Đặt ẩn phụ $t = t a n x$ , quy đồng, đưa về phương trình bậc hai ẩn t, giải phương trình suy ra các nghiệm t.

+) Giải phương trình lượng giác cơ bản của tan: $\tan x = \tan α \Leftrightarrow x = α + k π (k \in Z)$

Lời giải:

ĐK: ${\begin{cases} \sin x \neq 0 \\ \cos x \neq 0 \end{cases} \Leftrightarrow {\begin{cases} x \neq k π \\ x \neq \frac{π}{2} + k π \end{cases} \Leftrightarrow x \neq \frac{k π}{2} (k \in Z)$

$\begin{array}{l} \tan x - 2 \cot x + 1 = 0 \\ \Leftrightarrow \tan x - \frac{2}{\tan x} + 1 = 0 \\ \Leftrightarrow \tan^{2} x + \tan x - 2 = 0 \end{array}$

Đặt $t = t a n x$ thì phương trình trở thành

$\begin{array}{l} t^{2} + t - 2 = 0 \Leftrightarrow [\begin{array}{l} t = 1 \\ t = - 2 \end{array} \\ \Leftrightarrow [\begin{array}{l} \tan x = 1 \\ \tan x = - 2 \end{array} \\ \Leftrightarrow [\begin{array}{l} x = \frac{π}{4} + k π \\ x = \arctan (- 2) + k π \end{array} (k \in Z) (t m) \end{array}$

Bài 4 trang 37 sgk Đại số và Giải tích 11: Giải các phương trình sau:

Phương pháp giải:

Phương trình: $a \sin^{2} x + b \sin x \cos x + c \cos^{2} x = d$

TH 1: Xét $\cos x = 0$ có là nghiệm của phương trình hay không?

TH 2: Khi $\cos x \neq 0$ .

+ Bước 1: Chia cả 2 vế của phương trình cho $\cos^{2} x$

Ta được: $a \frac{\sin^{2} x}{\cos^{2} x} + b \frac{\sin x}{\cos x} + c = \frac{d}{\cos^{2} x}$

-Vì $\tan x = \frac{\sin x}{\cos x}; \frac{1}{\cos^{2} x} = \tan^{2} x + 1$ nên ta đưa phương trình về dạng:

$\begin{array}{l} a \tan^{2} x + b \tan x + c = d (1 + \tan^{2} x) \\ \Leftrightarrow (a - d) \tan^{2} x + b \tan x + c - d = 0 \end{array}$

+ Bước 2: Đặt $t = t a n x$ , giải phương trình bậc hai ẩn t và tìm các nghiệm t.

+ Bước 3: Giải phương trình lượng giác cơ bản của tan: $\tan x = \tan α \Leftrightarrow x = α + k π (k \in Z)$ và đối chiếu với điều kiện.

Lời giải:

$2 \sin^{2} x + \sin x \cos x - 3 \cos^{2} x = 0$

+ TH1: $\cos x = 0 \Leftrightarrow \sin^{2} x = 1$ , khi đó ta có $2.1 + 0 - 0 = 0$ (vô nghiệm)

$\Rightarrow \cos x \neq 0 \Rightarrow x \neq \frac{π}{2} + k π (k \in Z)$

+ TH2: Chia cả hai vế của phương trình cho $\cos^{2} x$ ta được:

$2 \frac{\sin^{2} x}{\cos^{2} x} + \frac{\sin x}{\cos x} - 3 = 0 \Leftrightarrow 2 \tan^{2} x + \tan x - 3 = 0$

Đặt $t = \tan x,$ khi đó phương trình trở thành: $2 t^{2} + t - 3 = 0 \Leftrightarrow [\begin{matrix} t = 1 \\ t = - \frac{3}{2} \end{matrix}$

Với $t = 1 \Leftrightarrow \tan x = 1 \Leftrightarrow x = \frac{π}{4} + k π (k \in Z) (t m)$

Với $t = - \frac{3}{2} \Rightarrow \tan x = - \frac{3}{2}$

$\Leftrightarrow x = \arctan (- \frac{3}{2}) + k π (k \in Z) (t m)$

Vậy nghiệm của phương trình là $x = \frac{π}{4} + k π (k \in Z)$ hoặc $x = \arctan (- \frac{3}{2}) + k π (k \in Z)$ .

Lời giải:

$3 \sin^{2} x - 4 \sin x \cos x + 5 \cos^{2} x = 2$

Khi $\cos x = 0 \Leftrightarrow \sin^{2} x = 1$ , khi đó ta có $3.1 - 0 + 0 = 2$ (vô nghiệm)

$\Rightarrow \cos x \neq 0 \Rightarrow x \neq \frac{π}{2} + k π (k \in Z)$

Chia cả hai vế của phương trình cho $\cos^{2} x$ ta được:

$\begin{aligned} 3 \frac{\sin^{2} x}{\cos^{2} x} - 4 \frac{\sin x}{\cos x} + 5 = \frac{2}{\cos^{2} x} \\ \Leftrightarrow 3 \tan^{2} x - 4 \tan x + 5 = 2 (\tan^{2} x + 1) \\ \Leftrightarrow \tan^{2} x - 4 \tan x + 3 = 0 \end{aligned}$

Đặt $t = \tan x,$ khi đó phương trình trở thành: $t^{2} - 4 t + 3 = 0 \Leftrightarrow [\begin{matrix} t = 1 \\ t = 3 \end{matrix}$

Với $t = 1 \Leftrightarrow \tan x = 1$

$\Leftrightarrow x = \frac{π}{4} + k π (k \in Z) (t m)$

Với $t = 3 \Rightarrow \tan x = 3$

$\Leftrightarrow x = \arctan 3 + k π (k \in Z) (t m)$

Vậy nghiệm của phương trình là $x = \frac{π}{4} + k π (k \in Z)$ hoặc $x = \arctan 3 + k π (k \in Z)$ .

Cách 2:

Ta có thể đưa về cùng dạng với câu a, như sau:

$\begin{array}{l} 3 \sin^{2} x - 4 \sin x \cos x + 5 \cos^{2} x = 2 \\ \Leftrightarrow 3 \sin^{2} x - 4 \sin x \cos x + 5 \cos^{2} x = 2 (\sin^{2} x + \cos^{2} x) \\ \Leftrightarrow 3 \sin^{2} x - 4 \sin x \cos x + 5 \cos^{2} x = 2 \sin^{2} x + 2 \cos^{2} x \\ \Leftrightarrow \sin^{2} x - 4 \sin x \cos x + 3 \cos^{2} x = 0 \end{array}$

Sau đó giải phương trình tương tự như câu a.

Lời giải:

$\begin{aligned} \sin^{2} x + \sin 2 x - 2 \cos^{2} x = \frac{1}{2} \\ \Leftrightarrow \sin^{2} x + 2 \sin x \cos x - 2 \cos^{2} x = \frac{1}{2} \\ \Leftrightarrow 2 \sin^{2} x + 4 \sin x \cos x - 4 \cos^{2} x = 1 \end{aligned}$

+TH1: $\cos x = 0 \Leftrightarrow \sin^{2} x = 1$ , khi đó ta có $2 + 0 - 0 = 1$ (vô nghiệm)

$\Rightarrow \cos x \neq 0 \Rightarrow x \neq \frac{π}{2} + k π (k \in Z)$

+TH2: Chia cả hai vế của phương trình cho $\cos^{2} x$ ta được:

$\begin{aligned} 2 \frac{\sin^{2} x}{\cos^{2} x} + 4 \frac{\sin x}{\cos x} - 4 = \frac{1}{\cos^{2} x} \\ \Leftrightarrow 2 \tan^{2} x + 4 \tan x - 4 = \tan^{2} x + 1 \\ \Leftrightarrow \tan^{2} x + 4 \tan x - 5 = 0 \end{aligned}$

Đặt $t = \tan x,$ khi đó phương trình trở thành: $t^{2} + 4 t - 5 = 0 \Leftrightarrow [\begin{matrix} t = 1 \\ t = - 5 \end{matrix}$

Với $t = 1 \Leftrightarrow \tan x = 1 \Leftrightarrow x = \frac{π}{4} + k π (k \in Z) (t m)$

Với $t = - 5 \Rightarrow \tan x = - 5$

$\Leftrightarrow x = \arctan (- 5) + k π (k \in Z) (t m)$

Vậy nghiệm của phương trình là $x = \frac{π}{4} + k π (k \in Z)$ hoặc $x = \arctan (- 5) + k π (k \in Z)$ .

Cách 2:

$\begin{array}{l} \sin^{2} x + \sin 2 x - 2 \cos^{2} x = \frac{1}{2} \\ \Leftrightarrow 2 \sin^{2} x + 2 \sin 2 x - 4 \cos^{2} x = 1 \\ \Leftrightarrow 2 \sin^{2} x + 2.2 \sin x \cos x - 4 \cos^{2} x = \sin^{2} x + \cos^{2} x \\ \Leftrightarrow \sin^{2} x + 4 \sin x \cos x - 5 \cos^{2} x = 0 \end{array}$

Sau đó thực hiện giải câu hỏi như câu a.

Lời giải:

$\begin{aligned} 2 \cos^{2} x - 3 \sqrt{3} \sin 2 x - 4 \sin^{2} x = - 4 \\ \Leftrightarrow 2 \cos^{2} x - 6 \sqrt{3} \sin x \cos x - 4 \sin^{2} x = - 4 \end{aligned}$

Khi $\cos x = 0 \Leftrightarrow \sin^{2} x = 1$ , khi đó ta có $0 + 0 - 4 = - 4 \Rightarrow x = \frac{π}{2} + k π (k \in Z)$ là nghiệm của phương trình.

Khi $\cos x \neq 0 \Rightarrow x \neq \frac{π}{2} + k π (k \in Z)$

Chia cả hai vế của phương trình cho $\cos^{2} x$ ta được:

$\begin{aligned} 2 - 6 \sqrt{3} \frac{\sin x}{\cos x} - 4 \frac{\sin^{2} x}{\cos^{2} x} = \frac{- 4}{\cos^{2} x} \\ \Leftrightarrow 2 - 6 \sqrt{3} \tan x - 4 \tan^{2} x = - 4 \tan^{2} x - 4 \\ \Leftrightarrow 6 \sqrt{3} \tan x = 6 \\ \Leftrightarrow \tan x = \frac{1}{\sqrt{3}} \\ \Leftrightarrow x = \frac{π}{6} + k π (k \in Z) \end{aligned}$

Vậy nghiệm của phương trình là $x = \frac{π}{2} + k π (k \in Z)$ hoặc $x = \frac{π}{6} + k π (k \in Z)$ .

Cách 2:

$\begin{array}{l} 2 \cos^{2} x - 3 \sqrt{3} \sin 2 x - 4 \sin^{2} x = - 4 \\ \Leftrightarrow 2 \cos^{2} x - 3 \sqrt{3} .2 \sin x \cos x - 4 \sin^{2} x = - 4 (\sin^{2} x + \cos^{2} x) \\ \Leftrightarrow 2 \cos^{2} x - 6 \sqrt{3} \sin x \cos x - 4 \sin^{2} x = - 4 \sin^{2} x - 4 \cos^{2} x \\ \Leftrightarrow 6 \cos^{2} x - 6 \sqrt{3} \sin x \cos x = 0 \\ \Leftrightarrow 6 \cos x (\cos x - \sqrt{3} \sin x) = 0 \\ \Leftrightarrow [\begin{array}{l} \cos x = 0 \\ \cos x - \sqrt{3} \sin x = 0 \end{array} \\ \Leftrightarrow [\begin{array}{l} \cos x = 0 \\ \cos x = \sqrt{3} \sin x \end{array} \\ \Leftrightarrow [\begin{array}{l} \cos x = 0 \\ \frac{\cos x}{\sin x} = \sqrt{3} \end{array} \\ \Leftrightarrow [\begin{array}{l} \cos x = 0 \\ \cot x = \sqrt{3} \end{array} \\ \Leftrightarrow [\begin{array}{l} x = \frac{π}{2} + k π \\ x = \frac{π}{6} + k π \end{array} \end{array}$

Bài 5 trang 37 sgk Đại số và Giải tích 11: Giải các phương trình sau:

a. cosx−√3sinx=√2

b. 3sin3x−4cos3x=5

c. 2sinx+2cosx−√2=0

d. 5cos2x+12sin2x−13=0

Phương pháp giải:

Phương pháp giải phương trình bậc nhất đối với sin và cos: $a \sin x + b \cos x = c (a^{2} + b^{2} > 0)$

- Chia cả hai vế cho $\sqrt{a^{2} + b^{2}}$ , khi đó phương trình có dạng:

$\frac{a}{\sqrt{a^{2} + b^{2}}} \sin x + \frac{b}{\sqrt{a^{2} + b^{2}}} \cos x = \frac{c}{\sqrt{a^{2} + b^{2}}}$

- Đặt ${\begin{cases} \frac{a}{\sqrt{a^{2} + b^{2}}} = \cos α \\ \frac{b}{\sqrt{a^{2} + b^{2}}} = \sin α \end{cases}$ và sử dụng công thức $\sin x \cos α + \cos x \sin α = \sin (x + α)$ sau đó giải phương trình lượng giác cơ bản của sin.

Hoặc đặt ${\begin{cases} \frac{a}{\sqrt{a^{2} + b^{2}}} = \sin α \\ \frac{b}{\sqrt{a^{2} + b^{2}}} = \cos α \end{cases}$ và sử dụng công thức $\sin x \sin α + \cos x \cos α = \cos (x - α)$ và giải phương trình lượng giác cơ bản của cos.

Lời giải:

$\begin{aligned} \cos x - \sqrt{3} \sin x = \sqrt{2} \\ \Leftrightarrow \frac{1}{2} \cos x - \frac{\sqrt{3}}{2} \sin x = \frac{\sqrt{2}}{2} \\ \Leftrightarrow \cos x \cos \frac{π}{3} - \sin x \sin \frac{π}{3} = \frac{\sqrt{2}}{2} \\ \Leftrightarrow \cos (x + \frac{π}{3}) = \cos \frac{π}{4} \\ \Leftrightarrow [\begin{matrix} x + \frac{π}{3} = \frac{π}{4} + k 2 π \\ x + \frac{π}{3} = - \frac{π}{4} + k 2 π \end{matrix} \\ \Leftrightarrow [\begin{matrix} x = - \frac{π}{12} + k 2 π \\ x = - \frac{7 π}{12} + k 2 π \end{matrix} (k \in Z) \end{aligned}$

Vậy nghiệm của phương trình là $x = - \frac{π}{12} + k 2 π$ hoặc $x = - \frac{7 π}{12} + k 2 π (k \in Z)$ .

Lời giải:

$\begin{aligned} 3 \sin 3 x - 4 \cos 3 x = 5 \\ \Leftrightarrow \frac{3}{5} \sin 3 x - \frac{4}{5} \cos 3 x = 1 \end{aligned}$

Đặt ${\begin{matrix} \sin α = \frac{3}{5} \\ \cos α = \frac{4}{5} \end{matrix}$ , phương trình trở thành

$\begin{aligned} \sin 3 x \sin α - \cos 3 x \cos α = 1 \\ \Leftrightarrow \cos 3 x \cos α - \sin 3 x \sin α = - 1 \\ \Leftrightarrow \cos (3 x + α) = - 1 \\ \Leftrightarrow 3 x + α = π + k 2 π \\ \Leftrightarrow 3 x = π - α + k 2 π \\ \Leftrightarrow x = \frac{π - α}{3} + \frac{k 2 π}{3} (k \in Z) \end{aligned}$

Vậy nghiệm của phương trình là $x = \frac{π - α}{3} + \frac{k 2 π}{3} (k \in Z)$ (Với $\sin α = \frac{3}{5}; \cos α = \frac{4}{5}$ ).

Chú ý:

Có thể đặt cách khác như sau:

Đặt ${\begin{matrix} \cos β = \frac{3}{5} \\ \sin β = \frac{4}{5} \end{matrix}$ , phương trình trở thành:

$\begin{array}{l} \sin 3 x \cos β - \cos 3 x \sin β = 1 \\ \Leftrightarrow \sin (3 x - β) = 1 \\ \Leftrightarrow 3 x - β = \frac{π}{2} + k 2 π \\ \Leftrightarrow 3 x = \frac{π}{2} + β + k 2 π \\ \Leftrightarrow x = \frac{π}{6} + \frac{β}{3} + \frac{k 2 π}{3} \end{array}$

Lời giải:

$\begin{aligned} 2 \sin x + 2 \cos x - \sqrt{2} = 0 \\ \Leftrightarrow 2 \sin x + 2 \cos x = \sqrt{2} \\ \Leftrightarrow \frac{2}{2 \sqrt{2}} \sin x + \frac{2}{2 \sqrt{2}} \cos x = \frac{\sqrt{2}}{2 \sqrt{2}} \\ \Leftrightarrow \frac{1}{\sqrt{2}} \sin x + \frac{1}{\sqrt{2}} \cos x = \frac{1}{2} \\ \Leftrightarrow \sin x \sin \frac{π}{4} + \cos x \cos \frac{π}{4} = \frac{1}{2} \\ \Leftrightarrow \cos (x - \frac{π}{4}) = \cos \frac{π}{3} \\ \Leftrightarrow [\begin{matrix} x - \frac{π}{4} = \frac{π}{3} + k 2 π \\ x - \frac{π}{4} = - \frac{π}{3} + k 2 π \end{matrix} \\ \Leftrightarrow [\begin{matrix} x = \frac{7 π}{12} + k 2 π \\ x = - \frac{π}{12} + k 2 π \end{matrix} (k \in Z) \end{aligned}$

Vậy nghiệm của phương trình là $x = \frac{7 π}{12} + k 2 π$ hoặc $x = - \frac{π}{12} + k 2 π (k \in Z) .$

Lời giải:

$\begin{aligned} 5 \cos 2 x + 12 \sin 2 x - 13 = 0 \\ \Leftrightarrow \frac{5}{13} \cos 2 x + \frac{12}{13} \sin 2 x = 1 \end{aligned}$

Đặt ${\begin{matrix} \frac{5}{13} = \cos α \\ \frac{12}{13} = \sin α \end{matrix}$ , khi đó phương trình trở thành

$\begin{aligned} \cos 2 x \cos α + \sin 2 x \sin α = 1 \\ \Leftrightarrow \cos (2 x - α) = 1 \\ \Leftrightarrow 2 x - α = k 2 π \\ \Leftrightarrow x = \frac{α}{2} + k π (k \in Z) \end{aligned}$

Vậy nghiệm của phương trình là $x = \frac{α}{2} + k π (k \in Z)$ với $\sin α = \frac{12}{13}; \cos α = \frac{5}{13}$ .

Bài 6 trang 37 sgk Đại số và Giải tích 11: Giải các phương trình sau:
a.

Phương pháp giải:

+) Tìm ĐKXĐ.

+) Sử dụng công thức $\frac{1}{\tan x} = \cot x = \tan (\frac{π}{2} - x)$

+) Đưa phương trình về dạng phương trình lượng giác cơ bản của tan: $\tan x = \tan α \Leftrightarrow x = α + k π (k \in Z)$

Lời giải:

$a) \tan (2 x + 1) \tan (3 x - 1) = 1$

ĐK: ${\begin{matrix} \cos (2 x + 1) \neq 0 \\ \cos (3 x - 1) \neq 0 \end{matrix}$

$\Leftrightarrow {\begin{cases} 2 x + 1 \neq \frac{π}{2} + k π \\ 3 x - 1 \neq \frac{π}{2} + k π \end{cases}$ $\Leftrightarrow {\begin{cases} 2 x \neq \frac{π}{2} - 1 + k π \\ 3 x \neq \frac{π}{2} + 1 + k π \end{cases}$ $\Leftrightarrow {\begin{cases} x \neq \frac{π}{4} - \frac{1}{2} + \frac{k π}{2} \\ x \neq \frac{π}{6} + \frac{1}{3} + \frac{k π}{3} \end{cases}$

$\begin{aligned} p t \Leftrightarrow \tan (2 x + 1) = \frac{1}{\tan (3 x - 1)} \\ \Leftrightarrow \tan (2 x + 1) = \cot (3 x - 1) \\ \Leftrightarrow \tan (2 x + 1) = \tan (\frac{π}{2} - 3 x + 1) \\ \Leftrightarrow 2 x + 1 = \frac{π}{2} - 3 x + 1 + k π \\ \Leftrightarrow 5 x = \frac{π}{2} + k π \\ \Leftrightarrow x = \frac{π}{10} + \frac{k π}{5} (k \in Z) (t m) \end{aligned}$

Vậy nghiệm của phương trình là $x = \frac{π}{10} + \frac{k π}{5} (k \in Z)$ .

Phương pháp giải:

+) Tìm ĐKXĐ.

+) Sử dụng công thức $\tan (a + b) = \frac{\tan a + \tan b}{1 - \tan a \tan b}$

+) Đặt $t = \tan x$ , đưa phương trình về dạng phương trình bậc hai ẩn t, giải phương trình tìm nghiệm t.

+) Giải phương trình lượng giác cơ bản của tan: $\tan x = \tan α \Leftrightarrow x = α + k π (k \in Z)$

Lời giải:

$b) \tan x + \tan (x + \frac{π}{4}) = 1$

ĐK: ${\begin{matrix} \cos x \neq 0 \\ \cos (x + \frac{π}{4}) \neq 0 \end{matrix}$

$\Leftrightarrow {\begin{cases} x \neq \frac{π}{2} + k π \\ x + \frac{π}{4} \neq \frac{π}{2} + k π \end{cases}$ $\Leftrightarrow {\begin{cases} x \neq \frac{π}{2} + k π \\ x \neq \frac{π}{4} + k π \end{cases}$

Khi đó,

$P T \Leftrightarrow \tan x + \frac{\tan x + \tan \frac{π}{4}}{1 - \tan x \tan \frac{π}{4}} = 1$

$\begin{aligned} \Leftrightarrow \tan x + \frac{\tan x + 1}{1 - \tan x} = 1 \\ \Leftrightarrow \tan x - \tan^{2} x + \tan x + 1 = 1 - \tan x \\ \Leftrightarrow \tan^{2} x - 3 \tan x = 0 \\ \Leftrightarrow \tan x (\tan x - 3) = 0 \\ \Leftrightarrow [\begin{matrix} \tan x = 0 \\ \tan x = 3 \end{matrix} \\ \Leftrightarrow [\begin{matrix} x = k π \\ x = \arctan 3 + k π \end{matrix} (k \in Z) (t m) \end{aligned}$

Vậy nghiệm của phương trình là $x = k π$ hoặc $x = \arctan 3 + k π (k \in Z)$ .

Lý thuyết Bài 3: Một số phương trình lượng giác thường gặp

I. PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC

1. Định nghĩa

Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng:

$a t + b = 0 (1)$

Trong đó, $a, b$ là các hằng số $(a \neq 0)$ và $t$ là một trong các hàm số lượng giác.

2. Cách giải

Chia cả hai vế cho $a$ ta được được $(1)$ về phương trình lượng giác cơ bản.

Ví dụ:

$\begin{array}{l} 2 \cos x - \sqrt{3} = 0 \\ \Leftrightarrow 2 \cos x = \sqrt{3} \\ \Leftrightarrow \cos x = \frac{\sqrt{3}}{2} = \cos \frac{π}{6} \\ \Leftrightarrow x = \pm \frac{π}{6} + k 2 π \end{array}$

3. Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác

Ví dụ:

$\begin{array}{l} 5 \sin x - \sin 2 x = 0 \\ \Leftrightarrow 5 \sin x - 2 \sin x \cos x = 0 \\ \Leftrightarrow \sin x (5 - 2 \cos x) = 0 \\ \Leftrightarrow [\begin{array}{l} \sin x = 0 \\ 5 - 2 \cos x = 0 \end{array} \\ \Leftrightarrow [\begin{array}{l} \sin x = 0 \\ \cos x = \frac{5}{2} (V N v i \frac{5}{2} > 1) \end{array} \\ \Leftrightarrow x = k π, k \in Z \end{array}$

II. PHƯƠNG TRÌNH BẬC HAI ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC

1. Định nghĩa

Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng

$a t^{2} + b t + c = 0 (a \neq 0)$

Trong đó $a, b, c$ là các hằng số và $t$ là một trong số các hàm số lượng giác.

2. Cách giải

- Đặt ẩn phụ và điều kiện cho ẩn (nếu có).

- Giải phương trình với ẩn phụ.

- Từ đó giải phương trình lượng giác cơ bản.

Ví dụ:

$\tan^{2} x - \tan x - 2 = 0 (1)$

Đặt $t = \tan x$ thì (1) là:

$t^{2} - t - 2 = 0 \Leftrightarrow [\begin{array}{l} t = - 1 \\ t = 2 \end{array}$

$\begin{array}{l} \Rightarrow [\begin{array}{l} \tan x = - 1 \\ \tan x = 2 \end{array} \\ \Leftrightarrow [\begin{array}{l} x = - \frac{π}{4} + k π \\ x = \arctan 2 + k π \end{array}, k \in Z \end{array}$

III. PHƯƠNG TRÌNH BẬC NHẤT ĐỐI VỚI $\sin x$ VÀ $\cos x$

Xét phương trình $a \sin x + b \cos x = c$

+) Chia hai vế phương trình cho $\sqrt{a^{2} + b^{2}}$

+) Gọi $α$ là góc lượng giác tạo bởi chiều dương của trục hoành với vecto $\vec{O M} = (a; b)$ thì phương trình trở thành một phương trình đã biết cách giải:

$\sin (x + α) = \frac{c}{\sqrt{a^{2} + b^{2}}}$

Chú ý : Để phương trình $\sin (x + a) = \frac{c^{2}}{\sqrt{a^{2} + b^{2}}}$ có nghiệm, điều kiện cần và đủ là

$| \frac{c^{2}}{\sqrt{a^{2} + b^{2}}} | \leq 1$

$\Leftrightarrow | c | \leq \sqrt{a^{2} + b^{2}}$

$\Leftrightarrow c^{2} \leq a^{2} + b^{2}$

Đó cũng là điều kiện cần và đủ để phương trình $a \sin x + b \cos x = c$ có nghiệm.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Toán Học Lớp 11

Giải Toán 11 Bài 3: Một số phương trình lượng giác thường gặp

Xem thêm các chương trình khác: