Giải Toán 11 Bài 1: Phương pháp quy nạp toán học

56 lượt xem

Bài trước

Bài sau

Chúng tôi giới thiệu Giải bài tập Toán 11 Bài 1: Phương pháp quy nạp toán học chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Phương pháp quy nạp toán học lớp 11.

Giải bài tập Toán 11 Bài 1: Phương pháp quy nạp toán học

Trả lời câu hỏi giữa bài

Trả lời hoạt động 1 trang 80 sgk Đại số và Giải tích 11: Xét hai mệnh đề chứa biến

P (n) : 3^{n} < n + 100

và

Q (n) : 2^{n} > n

với

n \in N *

a. Với $n = 1, 2, 3, 4, 5$ thì $P (n), Q (n)$ đúng hay sai?

b. Với mọi $n \in N *$ thì $P (n), Q (n)$ đúng hay sai?

Phương pháp giải:

Thay

n

vào các mệnh đề chứa biến và kiểm tra tính đúng sai của chúng

Lời giải:

Với $n = 1$ thì $P (1) :^{″} 3^{1} < 1 + 100^{″}$ đúng, $Q (1) :^{″} 2^{1} > 1^{″}$ đúng.

Với $n = 2$ thì $P (2) :^{″} 3^{2} < 2 + 100^{″}$ đúng, $Q (2) :^{″} 2^{2} > 2^{″}$ đúng.

Với $n = 3$ thì $P (3) :^{″} 3^{3} < 3 + 100^{″}$ đúng, $Q (3) :^{″} 2^{3} > 3^{″}$ đúng.

Với $n = 4$ thì $P (4) :^{″} 3^{4} < 4 + 100^{″}$ đúng, $Q (4) :^{″} 2^{4} > 4^{″}$ đúng.

Với $n = 5$ thì $P (5) :^{″} 3^{5} < 5 + 100^{″}$ sai, $Q (5) :^{″} 2^{5} > 5^{″}$ đúng.

Phương pháp giải:

Nhận xét tính đúng sai của các mệnh đề khi n bất kì thuộc N*.

Lời giải:

Với $P (n)$ : Do với $n = 5$ thì $P (n)$ sai nên $P (n)$ không đúng với mọi $n \in N^{*}$ .

Với $Q (n)$ : Quan sát $2^{n}$ ta thấy $2^{n}$ tăng rất nhanh so với $n$ nên $2^{n} > n$ với mọi $n \in N^{*}$ hay $Q (n)$ đúng với $n \in N^{*}$

Trả lời hoạt động 2 trang 81 sgk Đại số và Giải tích 11: Chứng minh rằng với

n \in N *

thì

$1 + 2 + 3 + \dots + n = \frac{n (n + 1)}{2}$

Phương pháp giải:

- Xét với $n = 1$ , chứng minh đẳng thức đúng với $n = 1$ .

- Giả sử đẳng thức đúng với $n = k \geq 1$ , chứng minh đẳng thức đúng với $n = k + 1$ .

Lời giải:

- Khi $n = 1, V T = 1$

$V P = \frac{1 (1 + 1)}{2} = 1$

- Giả sử đẳng thức đúng với $n = k \geq 1$ , nghĩa là:

$S_{k} = 1 + 2 + 3 + . . . + k = \frac{k (k + 1)}{2}$

Ta phải chứng minh rằng đẳng thức cũng đúng với $n = k + 1$ , tức là:

$S_{k + 1} = 1 + 2 + 3 + . . . + k + (k + 1)$ $= \frac{(k + 1) (k + 2)}{2}$

Thật vậy, từ giả thiết quy nạp ta có:

$S_{k + 1} = S_{k} + (k + 1)$ $= \frac{k (k + 1)}{2} + (k + 1)$

$= \frac{k (k + 1) + 2 (k + 1)}{2}$ $= \frac{(k + 1) (k + 2)}{2}$

Vậy đẳng thức đúng với mọi $n \in N *$

Trả lời hoạt động 3 trang 82 sgk Đại số và Giải tích 11: Cho hai số

3^{n} và 8 n với n \in N * .

a. So sánh $3^{n} và 8 n$ khi $n = 1, 2, 3, 4, 5.$

b. Dự đoán kết quả tổng quát và chứng minh bằng phương pháp quy nạp

Phương pháp giải:

Thay lần lượt các giá trị của

n

và so sánh.

Lời giải:

So sánh $3^{n} và 8 n$ với $n = 1, 2, 3, 4, 5$ .

$\begin{array}{l} n = 1 \Rightarrow 3^{1} = 3 < 8 = 8.1 \\ n = 2 \Rightarrow 3^{2} = 9 < 16 = 8.2 \\ n = 3 \Rightarrow 3^{3} = 27 > 24 = 8.3 \\ n = 4 \Rightarrow 3^{4} = 81 > 32 = 8.4 \\ n = 5 \Rightarrow 3^{5} = 243 > 40 = 8.5 \end{array}$

Phương pháp giải:

Từ các kết quả ở ý a) dự đoán kết quả tổng quát

3^{n} > 8 n

với mọi

n \geq 3

Lời giải:

Dự đoán kết quả tổng quát: $3^{n} > 8 n$ với mọi $n \geq 3$

- $n = 3$ , bất đẳng thức đúng

- Giả sử bất đẳng thức đúng với $n = k \geq 3$ , nghĩa là:

$3^{k} > 8 k$

Ta phải chứng minh rằng bất đẳng thức cũng đúng với $n = k + 1$ , tức là:

$3^{k + 1} > 8 (k + 1)$

Thật vậy, từ giả thiết quy nạp ta có:

$3^{k + 1} = 3^{k} .3 > 8 k .3 = 24 k = 8 k + 16 k$

$k \geq 3 \Rightarrow 16 k \geq 16.3 = 48 > 8$

Suy ra:

$3^{k + 1} > 8 k + 8 = 8 (k + 1)$

Vậy bất đẳng thức đúng với mọi $n \geq 3$

Bài tập (trang 82, 83 sgk Đại số và Giải tích 11)

Bài 1 trang 82 sgk Đại số và Giải tích 11: Chứng minh rằng với

n \in N^{*}

, ta có đẳng thức:

Phương pháp giải:

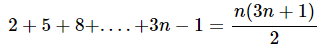
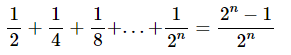
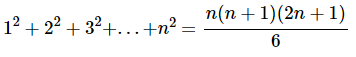
Vận dụng phương pháp chứng minh quy nạp toán học.

Bước 1: Chứng minh mệnh đề đúng với $n = 1$ .

Bước 2: Giả sử đẳng thức đúng đến $n = k \geq 1$ (giả thiết quy nạp). Chứng minh đẳng thức đúng đến $n = k + 1$ .

Khi đó đẳng thức đúng với mọi $n \in N^{*}$ .

Lời giải:

a. Với

n = 1

, vế trái chỉ có một số hạng là

2

, vế phải bằng

\frac{1. (3.1 + 1)}{2} = 2

Do đó hệ thức a) đúng với $n = 1$ .

Đặt vế trái bằng $S_{n}$

Giả sử đẳng thức a) đúng với $n = k \geq 1$ , tức là

$S_{k} = 2 + 5 + 8 + \dots + 3 k - 1$ $= \frac{k (3 k + 1)}{2}$

Ta phải chứng minh rằng a) cũng đúng với $n = k + 1$ , nghĩa là phải chứng minh

$S_{k + 1} = 2 + 5 + 8 + \dots . + 3 k - 1 + (3 (k + 1) - 1)$ $= \frac{(k + 1) (3 (k + 1) + 1)}{2}$

Thật vậy, từ giả thiết quy nạp, ta có:

$S_{k + 1} = [2 + 5 + 8 + \dots . + 3 k - 1] + (3 (k + 1) - 1)$

$= S_{k} + 3 k + 2$

$= \frac{k (3 k + 1)}{2} + 3 k + 2$

$= \frac{3 k^{2} + k + 6 k + 4}{2}$

$= \frac{3 k^{2} + 7 k + 4}{2}$ $= \frac{(k + 1) (3 k + 4)}{2}$ $= \frac{(k + 1) (3 k + 3 + 1)}{2}$ $= \frac{(k + 1) [3 (k + 1) + 1]}{2}$

(điều phải chứng minh)

Vậy theo nguyên lí quy nạp toán học, hệ thức a) đúng với mọi $n \in N^{*}$

b. Với

n = 1

, vế trái bằng

\frac{1}{2}

, vế phải bằng

\frac{1}{2}

, do đó hệ thức đúng với

n = 1

Đặt vế trái bằng $S_{n}$ _.

Giả sử hệ thức b) đúng với $n = k \geq 1$ , tức là

$S_{k} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + . . . + \frac{1}{2^{k}}$ $= \frac{2^{k} - 1}{2^{k}}$

Ta phải chứng minh $S_{k + 1} = \frac{2^{k + 1} - 1}{2^{k + 1}}$ .

Thật vậy, từ giả thiết quy nạp, ta có:

$S_{k + 1} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + . . . + \frac{1}{2^{k}} + \frac{1}{2^{k + 1}}$

$= S_{k} + \frac{1}{2^{k + 1}}$

$= \frac{2^{k} - 1}{2^{k}} + \frac{1}{2^{k + 1}}$ $= \frac{2 (2^{k} - 1) + 1}{2^{k + 1}}$ $= \frac{2^{k + 1} - 2 + 1}{2^{k + 1}} = \frac{2^{k + 1} - 1}{2^{k + 1}}$

(điều phải chứng minh)

Vậy theo nguyên lí quy nạp toán học, hệ thức b) đúng với mọi $n \in N^{*}$

c. Với

n = 1

, vế trái bằng

1

, vế phải bằng

\frac{1 (1 + 1) (2 + 1)}{6} = 1

nên hệ thức c) đúng với

n = 1

Đặt vế trái bằng $S_{n}$ _.

Giả sử hệ thức c) đúng với $n = k \geq 1$ , tức là

$S_{k} = 1^{2} + 2^{2} + 3^{2} + . . . + k^{2}$ $= \frac{k (k + 1) (2 k + 1)}{6}$

Ta phải chứng minh $S_{k + 1} = \frac{(k + 1) (k + 2) (2 (k + 1) + 1)}{6}$

Thật vậy, từ giả thiết quy nạp ta có:

$S_{k + 1} = 1^{2} + 2^{2} + 3^{2} + . . . + k^{2} + (k + 1)^{2}$

$= S_{k} + {(k + 1)}^{2}$

$= \frac{k (k + 1) (2 k + 1)}{6} + (k + 1)^{2}$

$\begin{array}{l} = \frac{k (k + 1) (2 k + 1) + 6 {(k + 1)}^{2}}{6} \\ = \frac{(k + 1) [k (2 k + 1) + 6 (k + 1)]}{6} \\ = \frac{(k + 1) (2 k^{2} + k + 6 k + 6)}{6} \\ = \frac{(k + 1) (2 k^{2} + 7 k + 6)}{6} \\ = \frac{(k + 1) (k + 2) (2 k + 3)}{6} \\ = \frac{(k + 1) (k + 2) (2 k + 2 + 1)}{6} \\ = \frac{(k + 1) (k + 2) [2 (k + 1) + 1]}{6} \end{array}$

(đpcm)

Vậy theo nguyên lí quy nạp toán học, hệ thức c) đúng với mọi $n \in N^{*}$ .

Bài 2 trang 82 sgk Đại số và Giải tích 11: Chứng minh rằng với

n \in N^{*}

ta luôn có:

n^{3} + 3 n^{2} + 5 n

chia hết cho

3

;

b. $4^{n} + 15 n - 1$ chia hết cho 9

c. $n^{3} + 11 n$ chia hết cho $6$ .

Phương pháp giải:

Vận dụng phương pháp chứng minh quy nạp toán học.

Bước 1: Chứng minh mệnh đề đúng với $n = 1$ .

Bước 2: Giả sử đẳng thức đúng đến $n = k \geq 1$ (giả thiết quy nạp). Chứng minh đẳng thức đúng đến $n = k + 1$ .

Khi đó đẳng thức đúng với mọi $n \in N^{*}$ .

Lời giải:

a. Đặt $S_{n} = n^{3} + 3 n^{2} + 5 n$

Với $n = 1$ thì $S_{1} = 1^{3} + {3.1}^{2} + 5.1 = 9$ chia hết cho $3$

Giả sử với $n = k \geq 1$ , $S_{k} = (k^{3} + 3 k^{2} + 5 k) ⋮$ $3$

Ta phải chứng minh rằng $S_{k + 1}$ $⋮$ $3$

Thật vậy :

$S_{k + 1} = {(k + 1)}^{3} + 3 {(k + 1)}^{2} + 5 (k + 1)$

$= k^{3} + 3 k^{2} + 3 k + 1 + 3 k^{2} + 6 k + 3 + 5 k + 5$

$= (k^{3} + 3 k^{2} + 5 k) + 3 k^{2} + 9 k + 9$

$= S_{k} + 3 (k^{2} + 3 k + 3)$

Theo giả thiết quy nạp thì $S_{k}$ $⋮$ $3$

Mà $3 (k^{2} + 3 k + 3) ⋮$ $3$ nên $S_{k + 1} ⋮$ $3$ .

Vậy $n^{3} + 3 n^{2} + 5 n$ chia hết cho $3$ với mọi $n \in N^{*}$ .

Cách khác:

Chứng minh trực tiếp.

Ta có:

$\begin{array}{l} n^{3} + 3 n^{2} + 5 n \\ = n . (n^{2} + 3 n + 5) \\ = n . (n^{2} + 3 n + 2 + 3) \\ = n . (n^{2} + 3 n + 2) + 3 n \\ = n . (n + 1) (n + 2) + 3 n . \end{array}$

Mà: $n (n + 1) (n + 2) ⋮ 3$ (tích của ba số tự nhiên liên tiếp)

và $3 n ⋮ 3$

$\Rightarrow n^{3} + 3 n^{2} + 5 n = n (n + 1) (n + 2) + 3 n ⋮ 3.$

Vậy $n^{3} + 3 n^{2} + 5 n$ chia hết cho $3$ với mọi $\forall n \in N *$

b. Đặt $S_{n} = 4^{n} + 15 n - 1$

Với $n = 1, S_{1} = 4^{1} + 15.1 - 1 = 18$ nên $S_{1} ⋮$ $9$

Giả sử với $n = k \geq 1$ thì $S_{k} = 4^{k} + 15 k - 1$ chia hết cho $9$ .

Ta phải chứng minh $S_{k + 1} ⋮$ $9$ .

Thật vậy, ta có:

$S_{k + 1} = 4^{k + 1} + 15 (k + 1) - 1$

$= {4.4}^{k} + 15 k + 15 - 1$

$= {4.4}^{k} + 15 k + 14$

$= {4.4}^{k} + 60 k - 45 k + 18 - 4$

$= ({4.4}^{k} + 60 k - 4) - 45 k + 18$

$= 4 (4^{k} + 15 k - 1) - 45 k + 18$

$= 4 S_{k} - 9 (5 k - 2)$

Theo giả thiết quy nạp thì $S_{k} ⋮$ $9$ nên $4 S_{k} ⋮ 9$

Mặt khác $9 (5 k - 2) ⋮$ $9$ , nên $S_{k + 1} ⋮ 9$

Vậy $(4^{n} + 15 n - 1) ⋮$ $9$ với mọi $n \in N^{*}$

c. Đặt $S_{n} = n^{3} + 11 n$

Với $n = 1$ , ta có $S_{1} = 1^{3} + 11.1 = 12$ nên $S_{1}$ $⋮$ $6$

Giả sử với $n = k \geq 1$ , $S_{k} = k^{3} + 11 k$ chia hết cho 6.

Ta phải chứng minh $S_{k + 1}$ $⋮$ 6

Thật vậy, ta có

$S_{k + 1} = {(k + 1)}^{3} + 11 (k + 1)$

$= k^{3} + 3 k^{2} + 3 k + 1 + 11 k + 11$

$= (k^{3} + 11 k) + (3 k^{2} + 3 k + 12)$

$= (k^{3} + 11 k) + 3 (k^{2} + k + 4)$

$= S_{k} + 3 (k^{2} + k + 4)$

Theo giả thiết quy nạp thì $S_{k}$ $⋮$ $6$ , mặt khác $k^{2} + k + 4 = k (k + 1) + 4$ là số chẵn nên $3 (k^{2} + k + 4)$ $⋮$ $6$ , do đó $S_{k + 1}$ $⋮$ $6$

Vậy $n^{3} + 11 n$ chia hết cho $6$ với mọi $n \in N^{*}$ .

Cách khác:

Chứng minh trực tiếp.

Ta có:

$\begin{array}{l} n^{3} + 11 n \\ = n^{3} - - n + 12 n \\ = n (n^{2} - - 1) + 12 n \\ = n (n - - 1) (n + 1) + 12 n . \end{array}$

Vì $n (n - - 1) (n + 1)$ là tích ba số tự nhiên liên tiếp nên có ít nhất 1 thừa số chia hết cho $2$ và 1 thừa số chia hết cho $3$

$n (n - 1) (n + 1) ⋮ 6$

Lại có: $12 n ⋮ 6$

$\Rightarrow n^{3} + 11 n = n (n - - 1) (n + 1) + 12 n ⋮ 6.$

Bài 3 trang 82 sgk Đại số và Giải tích 11: Chứng minh rằng với mọi số tự nhiên

n \geq 2

, ta có các bất đẳng thức:

3^{n} > 3 n + 1

2^{n + 1} > 2 n + 3

Phương pháp giải:

Vận dụng phương pháp chứng minh quy nạp toán học.

Bước 1: Chứng minh mệnh đề đúng với $n = 2$ .

Bước 2: Giả sử đẳng thức đúng đến $n = k \geq 2$ (giả thiết quy nạp). Chứng minh đẳng thức đúng đến $n = k + 1$ .

Khi đó đẳng thức đúng với mọi $n \in N^{*}$ .

Lời giải:

a. Với

n = 2

ta có:

3^{2} = 9 > 7 = 3.2 + 1

(đúng)

Giả sử bất đẳng thức đúng với $n = k \geq 2$ , tức là

$3^{k} > 3 k + 1$ (1).

Ta chứng minh bất đẳng thức đúng với $n = k + 1$ , tức là cần chứng minh: $3^{k + 1} > 3 (k + 1) + 1 = 3 k + 4$

Nhân hai vế của (1) với $3$ , ta được:

$3^{k + 1} > 9 k + 3$

$\Leftrightarrow 3^{k + 1} > 3 k + 4 + 6 k - 1$

Vì $k \geq 2 \Rightarrow 6 k - 1 \geq 11 > 0$ nên $3^{k + 1} > 3 k + 4 + 11 > 3 k + 4 = 3 (k + 1) + 1) .$

Tức là bất đẳng thức đúng với $n = k + 1$ .

Vậy $3^{n} > 3 n + 1$ với mọi số tự nhiên $n \geq 2$ .

b. Với

n = 2

thì

2^{2 + 1} = 8 > 7 = 2.2 + 3

(đúng)

Giả sử bất đẳng thức đúng với $n = k \geq 2$ , tức là

$2^{k + 1} > 2 k + 3$ (2)

Ta phải chứng minh nó cũng đúng với $n = k + 1$ , nghĩa là phải chứng minh

$2^{k + 2} > 2 (k + 1) + 3$

$\Leftrightarrow 2^{k + 2} > 2 k + 5$

Nhân hai vế của bất đẳng thức (2) với $2$ , ta được:

$2^{k + 2} > 4 k + 6$

$\Leftrightarrow 2^{k + 2} > 2 k + 5 + 2 k + 1$

Vì $k \geq 2 \Rightarrow 2 k + 1 > 0$ nên $2^{k + 2} > 2 k + 5$ .

Tức là bất đẳng thức đúng với $n = k + 1$ .

Vậy theo phương pháp quy nạp toán học thì bất đẳng thức $2^{n + 1} > 2 n + 3$ đúng với mọi số tự nhiên $n \geq 2$ .

Cách khác:

+ Với $n = 2$ thì bất đẳng thức $\Leftrightarrow 8 > 7$ (luôn đúng).

+ Giả sử bđt đúng khi $n = k \geq 2$ , nghĩa là $2^{k + 1} > 2 k + 3.$

Ta chứng minh đúng với $n = k + 1$ tức là chứng minh: $2^{k + 2} > 2 (k + 1) + 3.$

Thật vậy, ta có:

$\begin{array}{l} 2^{k + 2} = {2.2}^{k + 1} \\ > 2. (2 k + 3) = 4 k + 6 = 2 k + 2 + 2 k + 4. \\ > 2 k + 2 + 3 = 2. (k + 1) + 3 \end{array}$

(Vì $2 k + 4 > 3$ với mọi $k \geq 2$ )

$\Rightarrow (2)$ đúng với $n = k + 1$ .

Vậy $2^{n + 1} > 2 n + 3$ với mọi $n \geq 2$ .

Bài 4 trang 83 sgk Đại số và Giải tích 11: Cho tổng

S_{n} = \frac{1}{1.2} + \frac{1}{2.3} + . . . + \frac{1}{n (n + 1)}

với

n \in N^{*}

a. Tính

S_{1}, S_{2}, S_{3}

b. Dự đoán công thức tính tổng

S_{n}

và chứng minh bằng quy nạp.

Phương pháp giải:

Tính các giá trị

S_{1}; S_{2}; S_{3}

bằng cách thay lần lượt

n = 1; n = 2; n = 3

Lời giải:

Ta có:

$\begin{aligned} S_{1} = \frac{1}{1.2} = \frac{1}{2} \\ S_{2} = \frac{1}{1.2} + \frac{1}{2.3} = \frac{2}{3} \\ S_{3} = \frac{1}{1.2} + \frac{1}{2.3} + \frac{1}{3.4} = \frac{3}{4} \end{aligned}$

Phương pháp giải:

Dựa vào các giá trị $S_{1}; S_{2}; S_{3}$ tính được ở trên, dự đoán tổng $S_{n}$ .

Chứng minh kết quả vừa dự đoán bằng phương pháp quy nạp toán học.

Lời giải:

Từ câu a) ta dự đoán $S_{n} = \frac{n}{n + 1} (1)$ , với mọi $n \in N^{*}$

Ta sẽ chứng minh đẳng thức (1) bằng phương pháp quy nạp

Khi $n = 1$ , vế trái là $S_{1} = \frac{1}{2}$ vế phải bằng $\frac{1}{1 + 1} = \frac{1}{2}$ .

Vậy đẳng thức (1) đúng.

Giả sử đẳng thức (1) đúng với $n \geq 1$ , tức là

$S_{k} = \frac{1}{1.2} + \frac{1}{2.3} + . . . + \frac{1}{k (k + 1)} = \frac{k}{k + 1}$

Ta phải chứng minh đẳng thức đúng với $n = k + 1$ , nghĩa là phải chứng minh: $S_{k + 1} = \frac{k + 1}{k + 2}$

Ta có :

$S_{k + 1} = S_{k} + \frac{1}{(k + 1) (k + 2)}$ $= \frac{k}{k + 1} + \frac{1}{(k + 1) (k + 2)}$

$= \frac{k (k + 2) + 1}{(k + 1) (k + 2)}$ $= \frac{k^{2} + 2 k + 1}{(k + 1) (k + 2)}$

$= \frac{{(k + 1)}^{2}}{(k + 1) (k + 2)}$ $= \frac{k + 1}{k + 2}$

tức là đẳng thức (1) đúng với $n = k + 1$ .

Vậy đẳng thức (1) đã được chứng minh.

Chú ý:

Một cách dự đoán khác các em có thể tham khảo thêm như sau:

$\begin{array}{l} S_{1} = \frac{1}{1.2} = \frac{1}{1} - \frac{1}{2} = 1 - \frac{1}{2} \\ S_{2} = \frac{1}{1.2} + \frac{1}{2.3} = (\frac{1}{1} - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) = 1 - \frac{1}{3} \\ S_{3} = \frac{1}{1.2} + \frac{1}{2.3} + \frac{1}{3.4} = (\frac{1}{1} - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) + (\frac{1}{3} - \frac{1}{4}) = 1 - \frac{1}{4} \end{array}$

Dự đoán: $S_{n} = 1 - \frac{1}{n + 1}$ (1)

Ta chứng minh đẳng thức (1) bằng quy nạp

+ Với $n = 1$ thì (1) đúng.

+ Giả sử (1) đúng với $n = k$ , tức là

$S_{k} = \frac{1}{1.2} + \frac{1}{2.3} + . . . + \frac{1}{k (k + 1)} = 1 - \frac{1}{k + 1}$

Khi đó,

$\Rightarrow (1) đúng với n = k + 1, do đó đúng \forall n \in N * .$

Bài 5 trang 83 sgk Đại số và Giải tích 11: Chứng minh rằng số đường chéo của một đa giác lồi

n

cạnh là

\frac{n (n - 3)}{2}

Phương pháp giải:

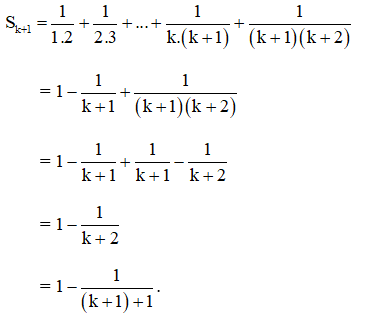
Ta chứng minh khẳng định đúng với mọi $n \in N^{*}$ , $n \geq 4$ .

Sử dụng phương pháp quy nạp toán học để chứng minh.

Lời giải:

Kí hiệu số đường chéo của đa giác $n$ cạnh là $C_{n}$ .

Ta chứng minh $C_{n} = \frac{n (n - 3)}{2}$ (1) với mọi $n \in N^{*}$ , $n \geq 4$ .

*) Với $n = 4$ , ta có tứ giác nên nó có 2 đường chéo.

Mặt khác $\frac{4 (4 - 3)}{2} = 2$ nên (1) đúng với $n = 4$ .

Vậy khẳng định đúng với $n = 4$ .

*) Giả sử (1) đúng với $n = k \geq 4$ , tức là $C_{k} = \frac{k (k - 3)}{2}$

*) Ta phải chứng minh (1) đúng với

n = k + 1

Tức là

C_{k + 1} = \frac{(k + 1) ((k + 1) - 3)}{2}

Xét đa giác lồi

k + 1

cạnh

Đa giác

k

cạnh

A_{1} A_{2} . . . A_{k}

có

\frac{k (k - 3)}{2}

đường chéo (giả thiết quy nạp).

Nối

A_{k + 1}

với các đỉnh

A_{2}, . . ., A_{k - 1}

, ta được thêm

k - 2

đường chéo.

Ngoài ra

A_{1} A_{k}

cũng là một đường chéo.

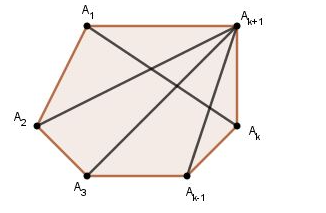
Vậy số đường chéo của đa giác $k + 1$ cạnh là

$\frac{k (k - 3)}{2} + k - 2 + 1$

$= \frac{k^{2} - 3 k}{2} + k - 1$

$= \frac{k^{2} - 3 k + 2 k - 2}{2}$

$= \frac{k^{2} - k - 2}{2}$

$= \frac{(k + 1) (k - 2)}{2}$

$= \frac{(k + 1) ((k + 1) - 3)}{2}$

Như vậy, khẳng định cũng đúng với đa giác $k + 1$ cạnh

Vậy bài toán đã được chứng minh.

Chú ý:

Trên đây là cách chứng minh bằng quy nạp, các em có thể dễ dàng chứng minhcông thức đó bằng kiến thức chương 2 như sau:

Cách 2: Đa giác lồi $n$ cạnh có $n$ đỉnh.

Chọn 2 điểm bất kì trong số các đỉnh của một đa giác ta được 1 cạnh hoặc 1 đường chéo của đa giác.

⇒ Tổng số cạnh và đường chéo của đa giác bằng:

$C_{n}^{2} = \frac{n!}{2! (n - 2)!}$ $= \frac{n (n - 1) (n - 2)!}{2 (n - 2)!} = \frac{n (n - 1)}{2}$

⇒ Số đường chéo của đa giác lồi có $n$ cạnh là:

$\frac{n (n - 1)}{2} - n = \frac{n^{2} - n - 2 n}{2}$ $= \frac{n^{2} - 3 n}{2} = \frac{n (n - 3)}{2}$

Vậy ta có đpcm.

Lý thuyết Bài Phương pháp quy nạp toán học

1. Để chứng minh một mệnh đề P(n) là đúng với mọi n ε N*, ta thường dùng phương pháp quy nạp toán học, được tiến hành theo hai bước như sau

Bài toán

Phương pháp quy nạp toán học

- Bước 1: Chứng minh $P (n)$ đúng với $n = 1$ .

- Bước 2: Với $k$ là một số nguyên dương tùy ý, giả sử $P (n)$ đúng với $n = k \geq 1$ , chứng minh $P (n)$ cũng đúng khi $n = k + 1$ .

Chú ý:

Đối với bài toán chứng minh $P (n)$ đúng với mọi $n \geq p$ với $p$ là số tự nhiên cho trước thì:

- Bước 1: Chứng minh $P (n)$ đúng với $n = p$ .

- Bước 2: Với $k \geq p$ là một số nguyên dương tùy ý, giả sử $P (n)$ đúng với $n = k$ , chứng minh $P (n)$ cũng đúng khi $n = k + 1$ .

Ví dụ: Chứng minh $n^{7} - n$ chia hết cho $7$ với mọi $n \in N^{*}$ .

Giải:

Đặt $P (n) = n^{7} - n$ .

- Với $n = 1$ thì $P (1) = 1^{7} - 1 = 0 ⋮ 7$ nên $P (1)$ đúng.

- Giả sử mệnh đề đúng với $n = k \in N^{*}$ , tức là $P (k) = (k^{7} - k) ⋮ 7$ .

Ta phải chứng minh mệnh đề đúng với $n = k + 1$ , tức là: $P (k + 1) = {(k + 1)}^{7} - (k + 1) ⋮ 7$

Ta có: ${(k + 1)}^{7} - (k + 1)$ $= C_{7}^{0} . k^{7} + C_{7}^{1} . k^{6} + C_{7}^{2} . k^{5} + C_{7}^{3} . k^{4}$ $+ C_{7}^{4} . k^{3} + C_{7}^{5} . k^{2} + C_{7}^{6} . k + C_{7}^{7} - (k + 1)$

$= k^{7} + 7 k^{6} + 21 k^{5} + 35 k^{4} + 35 k^{3}$ $+ 21 k^{2} + 7 k + 1 - k - 1$ $= (k^{7} - k) + 7 (k^{6} + 3 k^{5} + 5 k^{4} + 5 k^{3} + 3 k^{2} + k)$

Do $(k^{7} - k) ⋮ 7$ và $7 (k^{6} + 3 k^{5} + 5 k^{4} + 5 k^{3} + 3 k^{2} + k) ⋮ 7$ nên $P (k + 1) = {(k + 1)}^{7} - (k + 1) ⋮ 7$ .

Vậy mệnh đề đã cho đúng.

Xem thêm các chương trình khác:

Bài trước

Bài sau

Giải SGK, SBT, Chuyên đề Toán Học Lớp 11

Giải Toán 11 Bài 1: Phương pháp quy nạp toán học

1. Để chứng minh một mệnh đề P(n) là đúng với mọi n ε N*, ta thường dùng phương pháp quy nạp toán học, được tiến hành theo hai bước như sau

Xem thêm các chương trình khác: