1. Các kiến thức cần nhớ
Tứ giác
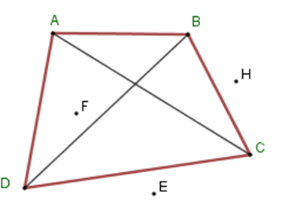
Định nghĩa : Tứ giác $ABCD$ là một hình gồm bốn đoạn thẳng $AB$ , $BC$ , $CD$ , $DA,$ trong đó bất kỳ hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Tứ giác lồi
Định nghĩa: Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác.
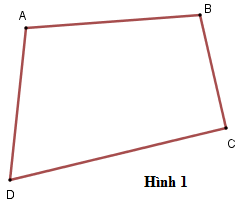
Ví dụ: Tứ giác \(ABCD\) (hình 1) là tứ giác lồi
Tổng các góc của một tứ giác
Định lý : Tổng bốn góc của một tứ giác bằng ${360^0}.$
Ví dụ: Tứ giác \(ABCD\) có \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
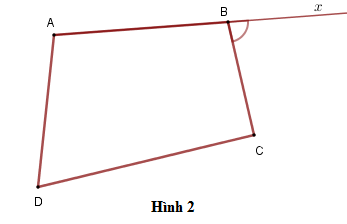
Chú ý: Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.
Ví dụ: Góc \(CBx\) là góc ngoài tại đỉnh \(B\) của tứ giác \(ABCD\) \( \Rightarrow \widehat {CBx} + \widehat {ABC} = 180^\circ .\)
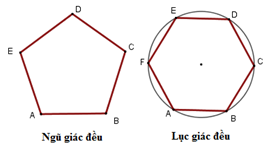
Đa giác đều
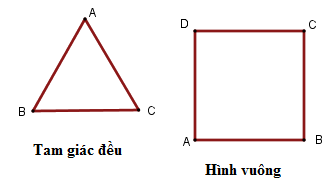
Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
2. Các dạng toán thường gặp
Dạng 1: Sử dụng tính chất về các góc của một tứ giác để tính góc
Phương pháp:
Ta sử dụng các kiến thức:
+ Tổng bốn góc của một tứ giác bằng${360^0}$ .
+ Góc ngoài của tứ giác là góc kề bù với một góc của tứ giác.
Dạng 2: Sử dụng bất đẳng thức tam giác để giải các bài toán liên quan đến các cạnh của một tứ giác
Phương pháp:
Ta sử dụng các kiến thức sau:
+ Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.
+ Trong một tam giác, hiệu độ dài hai cạnh bất kì bao giờ cũng nhỏ hơn độ dài cạnh còn lại.
+ Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh còn lại.
Nghĩa là: Trong tam giác \(ABC\) ta có $\left| {AB-AC} \right| < BC < AB + AC$.
