I. Các kiến thức cần nhớ
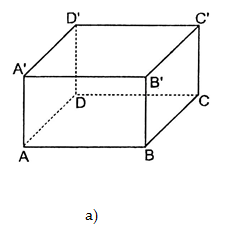
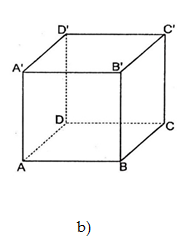
1. Định nghĩa: Hình hộp chữ nhật có $6$ mặt là hình chữ nhật (hình a). Hình lập phương là hình hộp chữ nhật có $6$ mặt là hình vuông (hình b).
2. Đường thẳng và mặt phẳng trong không gian
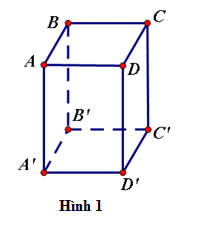
a. Hai đường thẳng phân biệt trong không gian có các vị trí:
- Cắt nhau nều có một điểm chung, chẳng hạn $AB$ cắt $BC$ (h.1).
- Song song, nếu cùng nằm trong một mặt phẳng và không có điểm chung, chẳng hạn $AB$ //$CD$ (h.1)
- Không cùng nằm trong một mặt phẳng nào, chẳng hạn $AB$ và $CC'$ (ta gọi chùng là hai đường thẳng chéo nhau).
b. Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
$AB{\rm{//}}CD,{\rm{ }}CD{\rm{//}}CD' \Rightarrow AB{\rm{//}}C'D'$ (h.1)
c. Nếu đường thẳng $\left( a \right)$ không nằm trong mặt phẳng $\left( P \right)$ và song song với một đường thẳng của mp $\left( P \right)$ thì đường thẳng $\left( a \right)$ song song với mp $\left( P \right).$
Chẳng hạn $AB$ // mp$\left( {A'B'C'D'} \right)$ (h.1)
d. Nếu mặt phẳng $\left( Q \right)$ chứa hai đường thẳng cắt nhau và chúng cùng song song với mp $\left( P \right)$ thì mp $\left( Q \right)$ song song với mp $\left( P \right).$
Chẳng hạn mp $\left( {ABCD} \right)$ // mp $\left( {A'B'C'D'} \right)$(h.1)
e. Hai mặt phẳng phân biệt có các vị trí:
- Song song, nếu chúng không có điểm chung nào.
- Cắt nhau, nếu tồn tại một điểm chung, khi đó chúng cắt nhau theo một đường thẳng đi qua điểm chung đó.
Chẳng hạn mp $\left( {ABCD} \right)$ cắt mp $\left( {BCC'B'} \right)$ theo đường thẳng $BC$ . (h.1).
II. Các dạng toán thường gặp
Dạng 1: Xác định các yếu tố và mối quan hệ giữa các yếu tố: điểm, đường thẳng, mặt phẳng của hình hộp chữ nhật.
Phương pháp:
Sử dụng các kiến thức học ở phần lý thuyết trên để làm bài.
Dạng 2: Tính toán các yếu tố cạnh, góc… của hình hộp chữ nhật
Phương pháp:
Sử dụng mối quan hệ giữa các cạnh và góc của hình hộp chữ nhật để tính toán.

