I. Các kiến thức cần nhớ
1. Đường thẳng vuông góc với mặt phẳng
- Nếu đường thẳng $\left( a \right)$ vuông góc với hai dường thẳng cắt nhau của mp $\left( P \right)$ thì đường thẳng $\left( a \right)$ vuông góc với mp $\left( P \right).$
- Nếu đường thẳng $\left( a \right)$ vuông góc với mp $\left( P \right)$ tại điểm $I$ thì nó vuông góc với mọi đường thẳng đi qua $I$ và nằm trong mp $\left( P \right).$
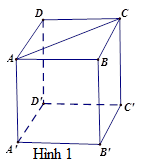
Trên hình 1, \(AA' \bot AB,AA' \bot AD\) nên \(AA' \bot mp(ABCD);AA' \bot AC\)
2. Mặt phẳng vuông góc với mặt phẳng
Nếu mp $\left( Q \right)$ chứa một đường thẳng vuông góc với mp $\left( P \right)$ thì mp $\left( Q \right)$ vuông góc với mp $\left( P \right).$
Trên hình 1, \(AA' \bot mp(ABCD)\) nên \((AA'B'B) \bot (ABCD)\)
3. Các công thức tính thể tích
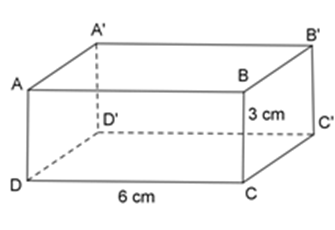
Thể tích của hình hộp chữ nhật $V = abc$ ($a,b,c$ là các kích thước của hình hộp chữ nhật)
Thể tích của hình lập phương: $V = {a^3}$ ($a$ là cạnh của hình lập phương).
2. Các dạng toán thường gặp
Dạng 1: Sử dụng mối quan hệ vuông góc để xác định các đường thẳng và mặt phẳng vuông góc.
Phương pháp:
Sử dụng các kiến thức
- Nếu đường thẳng $\left( a \right)$ vuông góc với hai dường thẳng cắt nhau của mp $\left( P \right)$ thì đường thẳng $\left( a \right)$ vuông góc với mp $\left( P \right).$
- Nếu đường thẳng $\left( a \right)$ vuông góc với mp $\left( P \right)$ tại điểm $I$ thì nó vuông góc với mọi đường thẳng đi qua $I$ và nằm trong mp $\left( P \right).$
- Nếu mp $\left( Q \right)$ chứa một đường thẳng vuông góc với mp $\left( P \right)$ thì mp $\left( Q \right)$ vuông góc với mp $\left( P \right).$
Dạng 2: Sử dụng các công thức tính thể tích để tính thê tích hình lập phương và hình hộp chữ nhật.
Phương pháp:
Ta sử dụng các công thức sau:
-Thể tích của hình hộp chữ nhật $V = abc$ ($a,b,c$ là các kích thước của hình hộp chữ nhật)
- Thể tích của hình lập phương: $V = {a^3}$ ($a$ là cạnh của hình lập phương).
Dạng 3: Các dạng khác
Phương pháp:
Ta sử dụng các công thức tính diện tich hình vuông, hình chữ nhật, định lý Pytago và các kiến thức về hình hộp chữ nhật, hình lập phương để tính toán.