I. Các kiến thức cần nhớ
1. Hình lăng trụ đứng
+ Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.
+ Các mặt phẳng chứa đáy của hình lăng trụ đứng là các mặt phẳng song song, các mặt bên vuông góc với hai mặt phẳng đáy, các cạnh bên vuông góc với hai mặt phẳng đáy. Độ dài một cạnh bên gọi là chiều cao.
+ Hình lăng trụ đứng có đáy là hình bình hành gọi là hình hộp đứng.
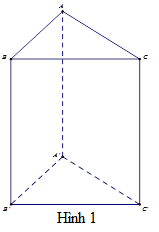
Ví dụ: Lăng trụ đứng tam giác \(ABC.A'B'C'\) .
2. Diện tích xung quanh hình lăng trụ đứng
Diện tích xung quanh của hình lăng trụ đứng bằng tích của chu vi đáy và chiều cao
\({s_{xq}} = 2.p.h\)
($p$ là nửa chu vi đáy, $h$ là chiều cao)
Diện tích toàn phần của hình lăng trụ đứng bằng tổng của diện tích xung quanh và diện tích hai đáy.
2. Thể tích hình lăng trụ đứng
Thể tích của hình lăng trụ đứng bằng tích của diện tích đáy và chiều cao
$V = S.h$ ( $S$ là diện tích đáy, $h$ là chiều cao).
II. Các dạng toán thường gặp
Dạng 1: Xác định mối quan hệ giữa các yếu tố của hình lăng trụ đứng (cạnh, góc, mặt phẳng)
Phương pháp:
Sử dụng quan hệ song song và vuông góc giữa các đường thẳng, các mặt phẳng, giữa đường thẳng và mặt phẳng và kiến thức về lăng trụ đứng.
Dạng 2: Tính độ dài cạnh, diện tích, thể tích...của hình lăng trụ đứng
Phương pháp:
Ta sử dụng các công thức
+ Diện tích xung quanh của hình lăng trụ đứng bằng tích của chu vi đáy và chiều cao \({S_{xq}} = 2.p.h\) ($p$ là nửa chu vi đáy, $h$ là chiều cao)
+ Diện tích toàn phần của hình lăng trụ đứng bằng tổng của diện tích xung quanh và diện tích hai đáy
+ Thể tích của hình lăng trụ đứng bằng tích của diện tích đáy và chiều cao $V = S.h$ ( $S$ là diện tích đáy, $h$ là chiều cao).

