Trả lời bởi giáo viên
Đáp án đúng: b
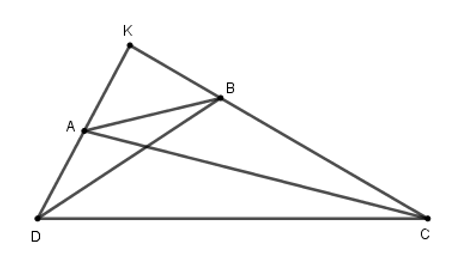
Gọi \(K\) là giao điểm \(AD,BC\).
Vì \(\widehat C + \widehat D = 90^\circ \) nên \(\widehat K = 90^\circ \).
Xét \(\Delta KAC\) vuông tại \(K\) ta có: \(A{C^2} = K{C^2} + K{A^2}\).
Xét \(\Delta KBD\) vuông tại \(K\) có: \(B{D^2} = K{B^2} + K{D^2}\).
Xét \(\Delta KBA\) vuông tại \(K\) có: \(B{A^2} = K{A^2} + K{B^2}\).
Xét \(\Delta KCD\) vuông tại \(K\) có: \(C{D^2} = K{C^2} + K{D^2}\).
Từ đó \(B{D^2} + A{C^2} = K{C^2} + K{A^2} + K{B^2} + K{D^2}\)\( = \left( {K{B^2} + K{A^2}} \right) + \left( {K{D^2} + K{C^2}} \right) = A{B^2} + D{C^2}\)
Hướng dẫn giải:
+ Gọi giao điểm của \(AD\) và \(BC\) là \(K.\)
+ Sử dụng định lý Pytago.

