Chọn phát biểu đúng?
A - đúng
B, C, D - sai
Lực ma sát nghỉ xuất hiện khi:
Lực ma sát nghỉ \(({\overrightarrow F _{m{\rm{s}}n}})\) chỉ xuất hiện khi có ngoại lực tác dụng lên vật. Ngoại lực này có xu hướng làm cho vật chuyển động nhưng chưa đủ để thắng lực ma sát.
Chọn phát biểu đúng.
A - sai vì: Lực ma sát nghỉ có giá luôn nằm trong mặt tiếp xúc giữa hai vật
B - sai vì: Lực ma sát nghỉ có chiều ngược chiều với ngoại lực
C - đúng
D - sai vì: Độ lớn của lực ma sát nghỉ\({F_{m{\rm{s}}n}} \le {\mu _n}N\)
Lực ma sát trượt xuất hiện:
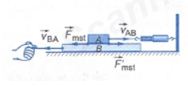
Lực ma sát trượt \(({\overrightarrow F _{m{\rm{st}}}})\) xuất hiện ở mặt tiếp xúc khi hai vật trượt trên bề mặt của nhau.
Chọn phát biểu sai?
A, B, C - đúng
D - sai vì: \({\mu _t}\) hầu như không phụ thuộc vào diện tích mặt tiếp xúc mà phụ thuộc vào tính chất của các mặt tiếp xúc (có nhẵn hay không, làm bằng vật liệu gì)
Chọn phát biểu đúng.
A - sai vì: trong một số trường hợp \({\mu _t} \approx {\mu _n}\)
B - đúng
C - sai vì hệ số ma sát trượt không phụ thuộc vào diện tích tiếp xúc mà phụ thuộc vào tính chất của mặt tiếp xúc
D - sai
Một vật trượt trên một mặt phẳng, khi tốc độ của vật tăng thì hệ số ma sát giữa vật và mặt phẳng:
Khi tốc độ của vật tăng thì hệ số ma sát giữa vật và mặt phẳng luôn không đổi
Lực ma sát trượt
Lực ma sát trượt: \({F_{m{\rm{st}}}} = {\mu _t}N\)=> phụ thuộc vào độ lớn của áp lực
Một vật có trọng lượng \(N\) trượt trên một mặt phẳng ngang. Biết hệ số ma sát trượt giữa vật và mặt phẳng là \(\mu \). Biểu thức xác định của lực ma sát trượt là:
Biểu thức xác định của lực ma sát trượt là: \({F_{m{\rm{s}}t}} = {\mu _t}N\)
Một người kéo một thùng hàng chuyển động, lực tác dụng vào người làm người đó chuyển động về phía trước là:
Lực tác dụng vào người làm người đó chuyển động về phía trước khi người đó kéo một thùng hàng chuyển động là lực mà mặt đất tác dụng vào bàn chân người kéo.
Khi một vật lăn trên mặt một vật khác:
Khi một vật lăn trên mặt một vật khác, lực ma sát lăn xuất hiện ở chỗ tiếp xúc giữa hai vật và có tác dụng cản trở sự lăn đó
Chọn phương án sai.
A, B, D - đúng
C - sai vì: Lực ma sát lăn cũng tỉ lệ với áp lực N giống như ma sát trượt nhưng hệ số ma sát lăn nhỏ hơn hệ số ma sát trượt hàng chục lần.
Chiều của lực ma sát nghỉ:
Ta có, lực ma sát nghỉ có chiều ngược chiều với ngoại lực hay chính là ngược chiều với vận tốc của vật
Một toa tàu có khối lượng \(80\) tấn chuyển động thẳng đều dưới tác dụng của lực kéo nằm ngang \(F = {6.10^4}N\). Lấy \(g = 10{\rm{ }}m/{s^2}\). Hệ số ma sát giữa tàu và đường ray là:
Ta có, toa tàu chuyển động thẳng đều => tổng các lực tác dụng lên toa tàu bằng 0
\(\overrightarrow F + \overrightarrow {{F_{m{\rm{s}}}}} = \overrightarrow 0 \) hay
\(\begin{array}{l}F = {F_{m{\rm{s}}}} \leftrightarrow F = \mu mg\\ \to \mu = \frac{F}{{mg}} = \frac{{{{6.10}^4}}}{{80000.10}} = 0,075\end{array}\)
Một xe tải có khối lượng \(5\) tấn đang chuyển động trên đường nằm ngang có hệ số ma sát của xe với mặt đường là \(0,2\). Lấy \(g = 10{\rm{ }}m/{s^2}\). Độ lớn của lực ma sát là:
Ta có, áp lực do xe tác dụng lên mặt đường chính bằng trọng lượng của xe
\(N = P = mg\)
\({F_{m{\rm{s}}}} = \mu N = \mu mg = 0,2.5000.10 = 10000N\)
Một đầu mát tạo ra lực kéo để kéo một toa xe có khối lượng \(5\) tấn, chuyển động với gia tốc \(0,3{\rm{ }}m/{s^2}\). Biết lực kéo của động cơ song song với mặt đường và hệ số ma sát giữa toa xe và mặt đường là \(0,02\). Lấy \(g = 10{\rm{ }}m/{s^2}\). Lực kéo của đầu máy tạo ra là:
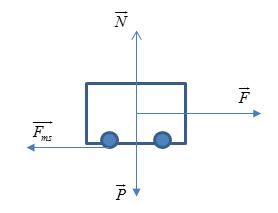
+ Các lực tác dụng lên xe gồm: Lực kéo \(\left( {\overrightarrow F } \right)\), lực ma sát \(\left( {\overrightarrow {{F_{m{\rm{s}}}}} } \right)\), trọng lực \(\left( {\overrightarrow P } \right)\), phản lực \(\left( {\overrightarrow N } \right)\)
+ Áp dụng định luật II-Niutơn, ta có: \(\overrightarrow F + \overrightarrow {{F_{m{\rm{s}}}}} + \overrightarrow P + \overrightarrow N = m\overrightarrow a \)
Chọn chiều dương trùng chiều chuyển động
Chiếu theo các phương ta được:
- Theo phương Oy: \(P = N\)
- Theo phương Ox: \(F - {F_{m{\rm{s}}}} = ma\)
\(\begin{array}{l} \to F = ma + {F_{m{\rm{s}}}} = ma + \mu N\\ \to F = ma + \mu mg = 5000.0,3 + 0,02.10.5000\\ = 2500N\end{array}\)
Một xe điện đang chạy với vận tốc \({v_0} = 36{\rm{ km/h}}\) thì hãm phanh đột ngột. Bánh xe không lăn nữa mà chỉ trượt trên đường ray. Kể từ lúc hãm phanh, xe điện còn đi được bao xa nữa thì dừng hẳn. Biết hệ số ma sát trượt giữa bánh xe và đường ray là \(0,2\). Cho \(g = 9,8{\rm{ m/}}{{\rm{s}}^2}\).
- Khi xe trượt trên đường ray, có 3 lực tác dụng lên xe:

+ Trọng lực: \(\overrightarrow P \)
+ Lực của đường ray: \(\overrightarrow Q \)
+ Lực ma sát trượt: \({\overrightarrow F _{_{mst}}}\)
- Theo định luật II Niutơn:
\(\overrightarrow P + \overrightarrow Q + {\overrightarrow F _{_{mst}}} = m\overrightarrow a \)
Mà: \(\overrightarrow P + \overrightarrow Q = \overrightarrow 0 \)
Nên: \({\overrightarrow F _{_{mst}}} = m\overrightarrow a \) (*)
- Chọn chiều dương là chiều chuyển động của xe.
\( - {F_{mst}} = ma\)
\( \Leftrightarrow - {\mu _t}mg = ma\)
\( \Rightarrow a = - {\mu _t}g = - 0,2.9,8 = - 1,96{\rm{ m/}}{{\rm{s}}^2}\)
- Quãng đường xe đi thêm được:
\({v^2} - v_0^2 = 2as \Rightarrow s = \frac{{{v^2} - v_0^2}}{{2a}} = \frac{{{0^2} - {{10}^2}}}{{2.( - 1,96)}} = 25,51{\rm{ m}}\)
Một vật trượt trên mặt đường nằm ngang, đi được một quãng đường 48 m thì dừng hẳn. Biết lực ma sát trượt có độ lớn bằng 0,06 lần trọng lượng của vật. Cho \(g = 10{\rm{ m/}}{{\rm{s}}^2}\). Cho chuyển động của vật là chậm dần đều. Tính vận tốc ban đầu của vật.
+ Khi vật trượt trên đường nằm ngang, có 3 lực tác dụng lên vật: \(\overrightarrow P \); \(\overrightarrow Q \) và \({\overrightarrow F _{mst}}\)
Theo định luật II Niutơn:
\(\overrightarrow P + \overrightarrow Q + {\overrightarrow F _{mst}} = m\overrightarrow a \)
Mà: \(\overrightarrow P + \overrightarrow Q = \overrightarrow 0 \)
Nên: \({\overrightarrow F _{mst}} = m\overrightarrow a \)
+ Chọn chiều dương là chiều chuyển động của vật
\( - {F_{mst}} = ma\)
Theo đề bài: \({F_{mst}} = 0,06P = 0,06mg\)
\( \Rightarrow - 0,06mg = ma\)
\( \Rightarrow a = - 0,06g = - 0,06.10 = - 0,6{\rm{ m/}}{{\rm{s}}^2}\)
+ Mặt khác:
\({v^2} - v_0^2 = 2as\)
Khi vật dừng lại thì \(v = 0\)
\( \Rightarrow - v_0^2 = 2.( - 0,6).48 = - 57,6\)
\({v_0} = \sqrt {57,6} = 7,6{\rm{ m/s}}\)
Một vận động viên môn hốc cây (môn khúc quân cầu) dùng gậy gạt quả bóng để truyền cho nó một tốc độ đầu 10m/s. Hệ số ma sát trượt giữa quả bóng với mặt băng là 0,1. Lấy g = 9,8m/s2. Quãng đường bóng đi được là :
Chọn chiều dương là chiều chuyển động của quả bóng.
Bóng chuyển động chậm dần đều dưới tác dụng của lực ma sát nên theo định luât II Niuton ta có:
\(\overrightarrow {{F_{ms}}} = m\overrightarrow a \,\,\,\left( * \right)\)
Chiếu (*) lên phương chuyển động ta có:
\(\begin{array}{l}{F_{ms}} = ma \Leftrightarrow - \mu N = ma \Leftrightarrow - \mu mg = ma\\ \Rightarrow a = - \mu g = - 0,1.9,8 = - 0,98m/{s^2}\end{array}\)
Áp dụng công thức liên hệ giữa s, v và a ta có:
\({v^2} - v_0^2 = 2as \Rightarrow s = \dfrac{{{v^2} - v_0^2}}{{2a}} = \dfrac{{{0^2} - {{10}^2}}}{{2.\left( { - 0,98} \right)}} = 51m\)
Vật khối lượng m nằm trên ván nằm ngang. Nâng dần một đầu tấm ván lên, hỏi góc hợp bởi mặt phẳng ván và phương ngang phải bằng bao nhiêu thì vật bắt đầu trượt. Biết hệ số ma sát trượt là 0,577.
Các lực tác dụng vào vật: trọng lực \(\overrightarrow P \); phản lực \(\overrightarrow Q \); lực ma sát \(\overrightarrow {{F_{ms}}} \)
Biểu diễn các lực tác dụng lên vật như hình vẽ:
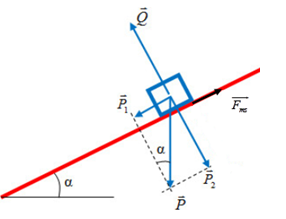
Để vật trượt trên tấm ván thì:
\({P_1} \ge {F_{ms}} \Leftrightarrow {P_1} \ge \mu N \Leftrightarrow P.\sin \alpha \ge \mu P.\cos \alpha \Rightarrow \dfrac{{\sin \alpha }}{{\cos \alpha }} \ge \mu \Leftrightarrow \tan \alpha \ge 0,577 \Rightarrow \alpha \ge {30^0}\)

