Một quyển sách được thả trượt từ đỉnh của một bàn nghiêng một góc α = 350 so với phương ngang. Hệ số ma sát trượt giữa mặt dưới của quyển sách với mặt bàn là µ = 0,5. Tìm gia tốc của quyển sách. Lấy g = 9,8 m/s2.
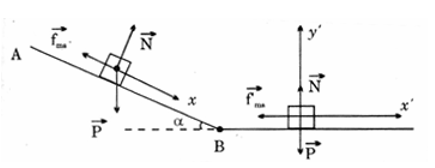
- Quyển sách chịu tác dụng của các lực: Trọng lực \(\overrightarrow P \); lực ma sát \(\overrightarrow {{f_{ms}}} \); phản lực \(\overrightarrow N \) của mặt bàn
- Phương trình định luật II Niu-tơn dưới dạng véc tơ:
\(\overrightarrow {{F_{ms}}} + \overrightarrow P + \overrightarrow N = m.\overrightarrow a \) (*)
- Chiếu (*) lên trục Ox và Oy ta được: \(\left\{ \begin{array}{l}P.sin\alpha - {f_{ms}} = ma\\ - {\rm{ }}Pcos\alpha + N = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}N = P.\cos \alpha \\P.sin\alpha - {f_{ms}} = ma\,\,\,\left( 2 \right)\end{array} \right.\)
Lực ma sát : \({f_{ms}} = \mu .N = \mu .P\cos \alpha = \mu mg.\cos \alpha \,\,\,\,\left( 3 \right)\)
Từ (2) và (3) ta có:
\(\begin{array}{l}ma = P\sin \alpha - {f_{ms}} = mg.\sin \alpha - \mu mg.\cos \alpha \\ \Rightarrow a = g.\left( {\sin \alpha - \mu .\cos \alpha } \right) = 9,8.\left( {\sin 35 - 0,5.\cos 35} \right) = 1,6m/{s^2}\end{array}\)
Một vật nhỏ khối lượng m chuyển động theo trục Ox (trên một mặt ngang), dưới tác dụng của lực \(\vec F\) nằm ngang có độ lớn không đổi. Xác định gia tốc chuyển động của vật khi hệ số ma sát trượt trên mặt ngang bằng µt ?
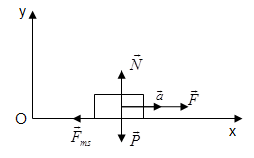
- Các lực tác dụng lên vật: Lực kéo \(\vec F\), lực ma sát \({\vec F_{ms}}\), trọng lực \(\vec P\), phản lực \(\vec N\)
- Chọn hệ trục tọa độ: Ox nằm ngang, Oy thẳng đứng hướng lên trên.
- Phương trình định luật II Niu-tơn dưới dạng véc tơ:
\(\vec F + {\vec F_{ms}} + \vec P + \vec N = m.\overrightarrow a \) (1)
- Chiếu (1) lên trục Ox, Oy ta được:
\(\left\{ \begin{array}{l}F-{F_{ms}} = ma\\ - P + N = 0\;\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \dfrac{{F-{F_{ms}}}}{m}\\P = N\end{array} \right.\)
Có: \({F_{ms}} = {\mu _t}.N = {\mu _t}.P = {\mu _t}.mg\)
→ Gia tốc chuyển động của vật: \(a = \dfrac{{F - {F_{ms}}}}{m} = \dfrac{{F - {\mu _t}.mg}}{m}\)
Một xe lăn có khối lượng 35kg, khi đẩy bằng một lực 70N có phương nằm ngang thì xe chuyển động thẳng đều. Khi chất lên xe một kiện hàng, phải tác dụng lực 100N nằm ngang để xe chuyển động thẳng đều. Biết xe chuyển động trên mặt phẳng ngang và lực ma sát giữa xe và mặt sàn là đáng kể, lấy \(g = 10m/{s^2}\). Khối lượng của kiện hàng là
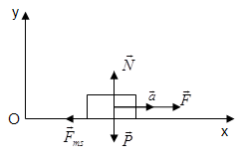
- Các lực tác dụng lên vật: Lực kéo \(\vec F\), lực ma sát \({\vec F_{ms}}\), trọng lực \(\vec P\), phản lực \(\vec N\)
- Chọn hệ trục tọa độ: Ox nằm ngang, Oy thẳng đứng hướng lên trên.
- Phương trình định luật II Niu-tơn dưới dạng véc tơ:
\(\vec F + {\vec F_{ms}} + \vec P + \vec N = m.\vec a\)
Xe chuyển động thẳng đều nên:
\(\vec F + {\vec F_{ms}} + \vec P + \vec N = 0\,\,\left( * \right)\)
- Chiếu (*) lên trục Ox, Oy ta được:
\(\left\{ {\begin{array}{*{20}{l}}{F - {F_{ms}} = 0}\\{ - P + N = 0\;}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{F = {F_{ms}}}\\{P = N}\end{array}} \right.\)
Lại có: \({F_{ms}} = \mu .N = \mu .mg \Rightarrow F = \mu .mg\)
+ Khi chưa chất hàng lên xe: \({F_1} = \mu {m_1}g\,\,\,\left( 1 \right)\)
+ Khi chất hàng lên xe: \({F_2} = \mu \left( {{m_1} + {m_2}} \right)g\,\,\,\left( 2 \right)\)
Lấy \(\dfrac{{\left( 2 \right)}}{{\left( 1 \right)}} \Leftrightarrow \dfrac{{{F_2}}}{{{F_1}}} = \dfrac{{{m_1} + {m_2}}}{{{m_1}}} \Leftrightarrow \dfrac{{100}}{{70}} = \dfrac{{35 + {m_2}}}{{35}} \Rightarrow {m_2} = 15kg\)
Xe khối lượng \(1\) tấn chuyển động thẳng đều lên dốc dài \(200m\), cao \(10m\) với vận tốc \(18km/h\). Biết hệ số ma sát có giá trị \(0,01\). Xác định lực kéo của động cơ để xe có trạng thái nêu trên

Chọn hệ trục tọa độ như hình vẽ:
Áp dụng định luật II Newton:
\(\overrightarrow {F_{ms}} + \overrightarrow P + \overrightarrow N + \overrightarrow F = m.\overrightarrow a \Leftrightarrow \overrightarrow {F_{ms}} + \overrightarrow P + \overrightarrow N + \overrightarrow F_1 + \overrightarrow F_2 = m.\overrightarrow a\,\,\,\left ( * \right )\)
Chiếu phương trình (*) lên Ox, Oy, ta có:
\(\left\{ \begin{array}{l}N = P_2 = P.\cos \alpha = mg\cos \alpha \\F - F_{ms} - P_1 = 0\Leftrightarrow F - \mu N - mg\sin \alpha = 0 \end{array} \right.\)
(do xe chuyển động thẳng đều)
\(\begin{array}{l} \Rightarrow F = \mu N + mg\sin \alpha = \mu mg\cos \alpha + mg\sin \alpha \\\,\,\,\,\,\,\,\,\,\,\, = mg.\left( {\mu \cos \alpha + \sin \alpha } \right)\\\,\,\,\,\,\,\,\,\,\,\, = {10^3}.10.\left( {0,01.\dfrac{{\sqrt {{{200}^2} - {{10}^2}} }}{{200}} + \dfrac{1}{{20}}} \right) = 600N\end{array}\)

