Bài tập các lực thường gặp

Phân tích các lực tác dụng lên vật ta có hình vẽ sau:

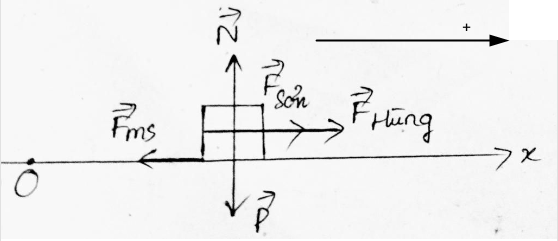
Chọn chiều dương như hình và chiếu các lực lên.

Áp dụng định luật II Newton ta được:

\({F_H} + {F_S} - {F_{m{\rm{s}}}} = ma\)

\(\begin{array}{l} \Leftrightarrow 450 + 200 - \mu mg = 400.0,5\\ \Leftrightarrow 650 - \mu .400.10 = 200\\ \Rightarrow \mu  \approx 0,1\end{array}\)

Lực ma sát trượt giữa vật và mặt phẳng tiếp xúc: \({F_{m{\rm{s}}}} = \mu N = \mu mg\)

theo đề bài ta có: \({F_{m{\rm{s}}}} = 0,3P\)

\(\begin{array}{l} \Leftrightarrow \mu mg = 0,3.m.g\\ \Leftrightarrow \mu  = 0,3\end{array}\)

Áp dụng định luật II Newton ta có:

\(\begin{array}{l} - {F_{m{\rm{s}}}} = ma\\ \Leftrightarrow  - \mu mg = ma\\ \Leftrightarrow a =  - 0,3.10 =  - 3\left( {m/{s^2}} \right)\end{array}\)

Ta có: \({v^2} - v_0^2 = 2a{\rm{s}}\)

Vận tốc ban đầu của vật là:

\(\begin{array}{l}v_0^2 = 2.120.3\\ \Rightarrow {v_0} \approx 26,8\left( {m/s} \right)\end{array}\)

Áp dụng phương trình vận tốc của vật ta có: \(v = {v_0} + at\)

\(\begin{array}{l} \Leftrightarrow 0 = 26,8 - 3t\\ \Leftrightarrow t \approx 9\left( s \right)\end{array}\)

Ta có lực đàn hồi và lực căng dây đều là những lực chống lại sự biến dạng đàn hồi của lò xo và sự căng của dây

Lực đàn hồi của lò xo có tác dụng làm cho lò xo có xu hướng lấy lại hình dạng và kích thước ban đầu

- Vật năng tác dụng lên một lực nén lên mặt bàn. Mặt bàn tác dạng một phản lực pháp tuyến lên vật nặng. Phản lực đó là một lực đàn hồi.

do nó được sinh ra bởi sự biến dạng của mặt bàn – bàn võng xuống.

Lực đàn hồi trong trường hợp này có phương thẳnng đứng

Theo định luật III Newton thì lực đàn hồi – lực bàn tác dụng lên vật = trọng lực của vật.

nên D không chính xác.

Ta có: \({F_{dh}} = k\Delta l\)

\( \Rightarrow \Delta l = \dfrac{{{F_{dh}}}}{k}\)

từ công thức trên ta có k càng lớn thì độ biến dạng càng nhỏ và ngược lại.

Ta có: tại các nơi ở gần mặt đất ta coi \(h \approx 0\) nên gia tốc trọng trường hay gia tốc rơi tự do được xác định như sau: \(g = \dfrac{{GM}}{{{R^2}}}\)

Ta có trọng lực được xem gần đúng là lực hút của Trái đất tác dụng lên vật đó, có chiều hướng về Trái đất, nó giảm khi đưa vật lên cao hoặc đưa vật từ cực bắc trở về xích đạo.

ta có thể giải thích dựa trên công thức \(P = G.\dfrac{{mM}}{{{{\left( {R + h} \right)}^2}}}\)

Còn trên Mặt Trăng, nhà du hành vũ trụ có thể nhảy lên rất cao so với khi nhảy ở Trái Đất vì ở đó trọng lượng của nhà du hành giảm.

Lực hấp dẫn giữa hai vật khi chưa thay đổi khối lượng và khoảng cách: \(F = G\dfrac{{{m_1}{m_2}}}{{{r^2}}}\)

Lực hấp dẫn giữa hai vật khi khối lượng và khoảng cách giữa chúng thay đổi: \(F = G.\dfrac{{\dfrac{{{m_1}}}{2}.\dfrac{{{m_2}}}{2}}}{{{{\left( {\dfrac{r}{2}} \right)}^2}}} = G\dfrac{{{m_1}{m_2}}}{{{r^2}}}\)

lực hấp dẫn khi đó không thay đổi

Quả cam đặt tại nơi có gia tốc g sẽ hút Trái đất với một lực có độ lớn bằng trọng lượng của nó là: \(P = mg\)

tại tâm Trái đất sẽ có gia tốc khác g nên trọng lực ( lực hút của Trái đất với quả cam ) không được tính bằng Mg được.

Ta có lực hút giữa hai vật là lực hấp dẫn giữa hai vật

ta có lực hấp dẫn giữa hai vật tỉ lệ thuận với tích hai khối lượng, tỉ lệ nghịch với bình phương khoảng cách giữa chúng

Lực hút tại thời điểm ban đầu: \(F = G\dfrac{{{m_1}{m_2}}}{{{r^2}}}\)

Lực hút khi thay đổi khoảng cách: \(F' = G\dfrac{{{m_1}{m_2}}}{{r{'^2}}}\)

theo bài ta có: \(F' = 6F\)

\(\begin{array}{l} \Rightarrow G\dfrac{{{m_1}{m_2}}}{{r{'^2}}} = 6G\dfrac{{{m_1}{m_2}}}{{{r^2}}}\\ \Leftrightarrow \dfrac{1}{{r{'^2}}} = 6\dfrac{1}{{{r^2}}} \Rightarrow {r^2} = 6{\rm{r}}{{\rm{'}}^2}\\ \Rightarrow r = \sqrt 6 r'\end{array}\)

hay khoảng cách giảm\(\sqrt 6 \) lần.

Ta có lực hấp dẫn giữa hai quả cầu là: \({F_{h{\rm{d}}}} = G\dfrac{{{m_1}{m_2}}}{{{r^2}}} \Rightarrow {\left( {{F_{h{\rm{d}}}}} \right)_{ma{\rm{x}}}} \Leftrightarrow {r_{\min }}\)

ta có: \({r_{\min }} \Leftrightarrow {R_1} + {R_2}\) khi hai quả cầu tiếp xúc nhau

khi đó lực hấp dẫn giữa 2 vật là: \({F_{h{\rm{d}}}} = G\dfrac{{{m_1}{m_2}}}{{{{({R_1} + {R_2})}^2}}} = \dfrac{{6,{{67.10}^{ - 11}}.200.200}}{{{{10}^2}}} = 2,{668.10^{ - 8}}N\)

Ban đầu, ta có: \(\left\{ \begin{array}{l}{m_1} = {m_2} = m = D{V_1} = D\frac{4}{3}\pi {r_1}^3\\{r_1} = {r_2}\\{F_{h{\rm{d}}}} = G\frac{{{m^2}}}{r^2} = F\end{array} \right.\)

Giả sử ta thay \({m_2} \to m{'_2}\)

Ta có:

\(r{'_2} = 2{{\rm{r}}_2} = 2{{\rm{r}}_1}\)

+ Khối lượng của

\(\begin{array}{l}m{'_2} = DV{'_2} = D\frac{4}{3}\pi {\left( {r{'_2}} \right)^3}\\ = D\frac{4}{3}\pi {\left( {2{{\rm{r}}_1}} \right)^3} = 8D\frac{4}{3}\pi {r_1}^3 = 8m\end{array}\)

+ Áp dụng biểu thức tính lực hấp dẫn, ta có:

 \({F_{h{\rm{d}}}}' = G\frac{{{m_1}m{'_2}}}{{{r^2}}} = G\frac{{m.8m}}{{{r^2}}} = 8F\)

Ta có lực hấp dẫn giữa hai vật là: \({F_{h{\rm{d}}}} = G\dfrac{{mm}}{{{r^2}}}\)

\(\begin{array}{l} \Leftrightarrow 1,{0672.10^{ - 7}} = 6,{67.10^{ - 11}}.\dfrac{{{m^2}}}{{0,{1^2}}}\\ \Rightarrow m = 4\left( {kg} \right)\end{array}\)

Khi \(h = 0\) ta có gia tốc rơi tự do tại bề mặt Mặt trăng là: \({g_0} = \dfrac{{GM}}{{{R^2}}}\)

tại nơi có độ cao 3480m ta có:

\(g = \dfrac{{GM}}{{{{\left( {R + h} \right)}^2}}} = \dfrac{{GM}}{{{{\left( {R + 2{\rm{R}}} \right)}^2}}} = \dfrac{{{g_0}}}{9}\)

Gia tốc tại mặt đất: \(g = \dfrac{{GM}}{{{R^2}}}\)

Gọi nơi có \({g_h}\) là độ cao h

khi đó gia tốc được tính bằng công thức \(g' = \dfrac{{GM}}{{{{\left( {{\rm{R}} + h} \right)}^2}}}\)

Lập tỉ số ta có: \(\dfrac{{g'}}{g} = \dfrac{{{R^2}}}{{{{\left( {R + h} \right)}^2}}}\)

\( \Rightarrow \dfrac{{R + h}}{R} = \sqrt {\dfrac{g}{{g'}}}  = \sqrt {\dfrac{{9,8}}{{8,9}}} \)

\(\begin{array}{l} \Rightarrow \dfrac{h}{R} = \sqrt {\dfrac{{9,8}}{{8,9}}}  - 1\\ \Rightarrow h = R\left( {\sqrt {\dfrac{{9,8}}{{8,9}}}  - 1} \right) = 315,8km \approx 316km\end{array}\)

Trọng lực của vật là lực hút của Trái đất lên vật, luôn hướng xuống và có độ lớn \(P = mg\)

Trọng lượng là tổng các lực quán tính trong hệ quy chiếu phi quán tính gắn với mặt đất, trong đó quan trọng nhất là lực quán tính li tâm gây ra bởi chuyển động quay quanh trục Trái đất.

nên ta có trọng lượng là tổng của lực hấp dẫn tác dụng lên vật và lực quán tính li tâm xuất hiện do sự quay của Trái đất quanh trục.

Tại mặt đất ta có trọng lượng: \({P_1} = G\dfrac{{mM}}{{{R^2}}}\left( 1 \right)\)

ở độ cao cách tâm Trái đất một đoạn 2R

\( \Rightarrow h = R\)

khi đó ta có: \({P_2} = G\dfrac{{mM}}{{{{(R + h)}^2}}} = G\dfrac{{mM}}{{4{{\rm{R}}^2}}}\left( 2 \right)\)

từ (1) và (2): \( \Rightarrow {P_2} = \dfrac{{{P_1}}}{4} = 2,5N\)

Biểu thức tính lực ma sát là: \(\mathop {{F_{mst}}}\limits^{}  = {\mu _t}\mathop N\limits^{} \)