Với giải HĐ2 trang 7 Toán 11 Tập 1 Kết nối tri thức chi tiết trong Bài 1: Giá trị lượng giác của góc lượng giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 1: Giá trị lượng giác của góc lượng giác
HĐ2 trang 7 Toán 11 Tập 1: Nhận biết hệ thức Chasles
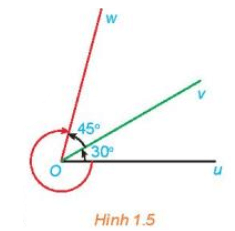
Cho ba tia Ou, Ov, Ow với số đo của các góc hình học uOv và vOw lần lượt là 30° và 45°.
a) Xác định số đo của ba góc lượng giác (Ou, Ov), (Ov, Ow) và (Ou, Ow) được chỉ ra ở Hình 1.5.
b) Với các góc lượng giác ở câu a, chứng tỏ rằng có một số nguyên k để
sđ(Ou, Ov) + sđ(Ov, Ow) = sđ(Ou, Ow) + k360°.
Lời giải:
a) Quan sát Hình 1.5 ta có:
sđ(Ou, Ov) = 30°;
sđ(Ov, Ow) = 45°;
sđ(Ou, Ow) = – (360° – 30° – 45°) = – 285°.
b) Ta có: sđ(Ou, Ov) + sđ(Ov, Ow) = 30° + 45° = 75°.
Lại có: – 285° + 1 . 360° = 75°.
Vậy tồn tại một số nguyên k = 1 để sđ(Ou, Ov) + sđ(Ov, Ow) = sđ(Ou, Ow) + k360°.