Phương trình chuyển động của một vật trên một đường thẳng có dạng \(x = 4{t^2} - 3t + 7(m;s)\). Điều nào sau đây là sai?
Ta có: Gia tốc của vật là: a = 8m/s2
=> A - sai
Một xe chuyển động nhanh dần đều đi được S = 24m, S2 = 64m trong 2 khoảng thời gian liên tiếp bằng nhau là 4s. Xác định vận tốc ban đầu và gia tốc.
Quãng đường vật đi được trong 2 khoảng thời gian liên tiếp bằng nhau là 4s là :
\(\begin{array}{l}{S_1}\; = {v_{01}}{t_1} + \frac{1}{2}a{t_1}^24.{v_{01}} + 8a = 24{\rm{ }}\left( 1 \right)\\{S_2} = {v_{02}}{t_2} + \frac{1}{2}a{t_2}^2\;4.{v_{01}} + 8a = 64{\rm{ }}\left( 2 \right)\end{array}\)
Mà \({v_{02}} = {v_1} = {v_{01}} + a{t_2}\left( 3 \right)\)
Giải (1), (2), (3) ta được : \({v_{01}} = 1m/s,\;a = 2,5m/{s^2}\)
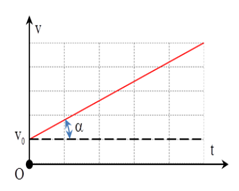
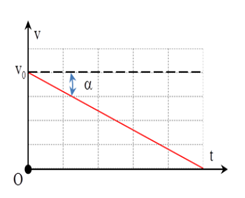
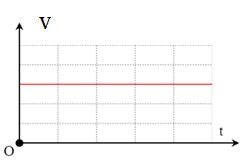
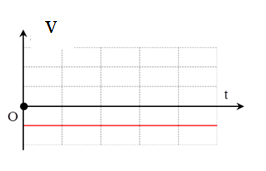
Đồ thị v - t nào sau đây là đồ thị trong đó a > 0
Đồ thị v - t trong đó a > 0 là đồ thị A