Chọn câu sai: Khi một chất điểm chuyển động thẳng biến đổi điều thì nó:
A, C, D - đúng
B - sai vì trong chuyển động biến đổi đều vận tốc thay đổi theo phương trình: \(v = {v_0} + at\)
Một vật chuyển động thẳng có phương trình \(x = 30 + 4t - {t^2}(m;s)\) . Tính quãng đường vật đi từ thời điểm $t_1 = 1s$ đến thời điểm $t_2 = 3s$?
Từ phương trình tọa độ - thời gian ta thu được phương trình vận tốc \(v = 4 - 2t \to v = 0 \leftrightarrow t = 2{\rm{s}}\) , vật sẽ đổi chiều chuyển động sau $2s$.
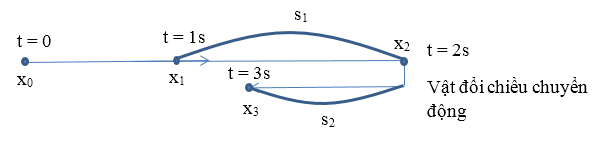
Do vậy quãng đường đi được của vật được tính:
\(s = {s_1} + {s_2} = \left| {{x_2} - {x_1}} \right| + \left| {{x_3} - {x_2}} \right| = \left| {4 - 3} \right| + \left| {3 - 4} \right| = 2m\)
Chọn phương án đúng. Chuyển động rơi tự do có:
A - sai vì: chuyển động rơi tự do có phương thẳng đứng
B - đúng
C, D - sai vì chuyển động rơi tự do là chuyển động nhanh dần đều.
Hãy nêu đầy đủ các tính chất đặc trưng cho chuyển động thẳng nhanh dần đều
Các đặc trưng của chuyển động thẳng nhanh dần đều gồm cả A, B và C
Chọn câu sai? Chất điểm sẽ chuyển động thẳng nhanh dần đều nếu
Chất điểm chuyển động nhanh dần đều nếu a và v cùng dấu (a.v > 0)
=> Phương án C - sai vì: a.v0 < 0
Một vật chuyển động thẳng có phương trình vận tốc \(v = 2 - 2t\).Tốc độ trung bình của vật sau $4s$ kể từ lúc bắt đầu chuyển động là:
Ta để ý rằng sau $1s$ vật đã đổi chiều chuyển động
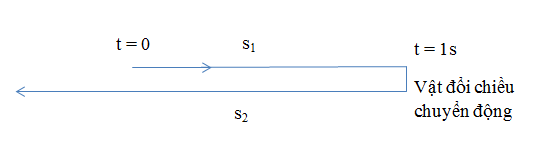
Chọn gốc thời gian là vị trí vật bắt đầu chuyển động, ta có:
Phương trình li độ của vật: \(x = {v_0}t + \dfrac{1}{2}a{t^2} = 2t - {t^2}\)
+ Tại \(t = 0\): \({x_0} = 0\)
+ Tại \(t = 1s\): \({x_1} = 1m\)
+ Tại \(t = 4s\): \({x_4} = - 8m\)
=> Ta suy ra:
+ Quãng đường vật đi được trong giây thứ nhất là: \({s_1} = {x_1} - {x_0} = 1m\)
+ Quãng đường vật đi được từ giây thứ 1 đến giây thứ 4 là: \({s_2} = \left| {{x_4} - {x_1}} \right| = \left| { - 8 - 1} \right| = 9m\)
=> Quãng đường vật đi được sau 4 s: \(s = {s_1} + {s_2} = 1 + 9 = 10m\)
Tốc độ trung bình \({v_{tb}} = \dfrac{s}{t} = \dfrac{{10}}{{1 + 3}} = 2,5m/s\)
Trong công thức tính quãng đường đi được của chuyển động thẳng chậm dần đều cho đến khi dừng lại: \(s = {v_0}t + \frac{1}{2}a{t^2}\) thì:
Trong chuyển động thẳng chậm dần đều thì vận tốc và gia tốc ngược dấu nhau, quãng đường là đại lượng không âm
Chọn câu đúng trong các câu sau :
A - sai vật nào có lực cản nhỏ hơn sẽ rơi nhanh hơn
B - sai vì trong chân không, các vật rơi như nhau
C - đúng
D - sai vì ở cùng một nơi trên Trái Đất, các vật đều rơi tự do với cùng một gia tốc
Một vật rơi tự do không vận tốc đầu từ một điểm A vào lúc t = 0. Phương trình của vật khi
chọn gốc toạ độ là vị trí O ở dưới A một khoảng 196m, chiều dương hướng xuống là : (g = 9,8m/s2)
Ta có:
+ Vật rơi không vận tốc đầu: \( \to {v_0} = 0\)
Gốc tọa độ tại O ở phía dưới A một đoạn 196m, chiều dương hướng xuống
+ Tọa độ ban đầu của vật: \({y_0} = - 196m\)
=> Phương trình chuyển động của vật: \(y = - 196 + \frac{1}{2}.9,8{t^2} = 4,9{t^2} - 196\left( m \right)\)
Một vật rơi tự do tại nơi có \(g = 10m/{s^2}\). Trong \(2\) giây cuối vật rơi được \(180m\). Tính thời gian rơi và độ cao buông vật?
+ Trong \(2\left( s \right)\) cuối cùng quãng đường vật đi được là \(180{\rm{ }}m\) ta có:
\(\begin{array}{l}\Delta S = {S_t} - {S_{t - 2}} \\= 180 = \dfrac{{g{t^2}}}{2} - \dfrac{{g.{{\left( {t - 2} \right)}^2}}}{2} \\\Rightarrow {t^2} - {\left( {t - 2} \right)^2} = 36\\ \Rightarrow 4t -4 = 36 \Rightarrow t = 10\left( s \right)\end{array}\)
+ Độ cao buông vật là: \(s = \dfrac{{g{t^2}}}{2}\) $= 500 m$
Một vật chuyển động nhanh dần đều với vận tốc ban đầu $v_0 = 0$. Trong giây thứ nhất vật đi được quãng đường $s_1 = 3m$. Trong giây thứ hai vật đi được quãng đường $s_2$ bằng:
Chọn gốc tọa độ tại vị trí vật bắt đầu chuyển động
Gốc thời gian là lúc vật bắt đầu chuyển động
Ta có:
+ Phương trình chuyển động của vật là: $s = \dfrac{1}{2}a{t^2}$
+ Quãng đường vật đi được trong giây thứ nhất: \({s_1} = \dfrac{1}{2}a{.1^2} = 3 \to a = 6m/{s^2}\)
+ Quãng đường vật đi được trong hai giây đầu là \({s_2} = \dfrac{1}{2}{6.2^2} = 12m\)
=> Quãng đường vật đi được trong giây thứ 2 là: \(s = {s_2} - {s_1} = 12 - 3 = 9m\).
Một đoàn tàu đang chạy với vận tốc 72km/h thì hãm phanh, chạy chậm dần đều sau 10s vận tốc giảm xuống còn 54km/h . Hỏi sau bao lâu thì tàu dừng lại hẳn
Gia tốc của xe : \(a = \frac{{15 - 20}}{{10}} = - 0,5m/{s^2}\)
Phương trình vận tốc của vật: \(v = 20 - 0,5t\)
Xe dừng lại hẳn khi: \(v = 0 \leftrightarrow 20 - 0,5t = 0 \to t = 40{\rm{s}}\)
Một vật rơi tự do từ độ cao h so với mặt đất, cho gia tốc rơi tự do g = 10 m/s2. Biết trong 1 s cuối cùng vật rơi được quãng đường bằng với quãng đường rơi được trong \(\sqrt 3 s\) đầu tiên. Giá trị của h bằng
Quãng đường đi được của vật rơi tự do trong thời gian \(\sqrt{3}s\)đầu tiên
\(s=\frac{1}{2}.g.{{t}^{2}}=\frac{1}{2}.g.3=1,5g\)
Trong giây cuối cùng quãng đường vật đi được là
\({{S}_{c}}=h-\frac{1}{2}.g.{{({{t}_{h}}-1)}^{2}}\)
với \({{t}_{h}}\) là thời gian vật rơi chạm đất: \({{t}_{h}}=\sqrt{\frac{2h}{g}}\text{ }\)
Vậy ta có: \({{S}_{c}}=h-\frac{1}{2}.g.{{\left( \sqrt{\frac{2h}{g}}-1 \right)}^{2}}=\sqrt{2gh}-\frac{1}{2}g\)
Mà \(s={{S}_{c}}\) nên ta có:
\(\sqrt{2gh}-0,5g=1,5g\Leftrightarrow \sqrt{2gh}=2g\Leftrightarrow h=2g=20m\)
Lúc 7 h, hai ôtô bắt đầu khởi hành từ hai điểm A, B cách nhau 2400 m, chuyển động nhanh dần đều và ngược chiều nhau. ôtô đi từ A có gia tốc 1 m/s2, còn ôtô từ B có gia tốc 2 m/s2. Chọn chiều dương hướng từ A đến B, gốc thời gian lúc 7 h. Xác định vị trí hai xe gặp nhau:
Ta có:
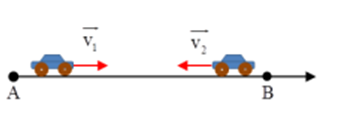
+ Phương trình chuyển động của hai ô tô lúc này là: \(\left\{ \begin{array}{l}A:{x_1} = \dfrac{1}{2}{t^2}\\B:{x_2} = 2400 - {t^2}\end{array} \right.\)
+ Khi hai xe gặp nhau: \({x_1} = {x_2} \leftrightarrow \dfrac{1}{2}{t^2} = 2400 - {t^2} \to t = 40{\rm{s}}\)
Vậy vị trí hai xe gặp cách A một khoảng: \(x = {x_1}(t = 40{\rm{s}}) = \dfrac{1}{2}{.40^2} = 800m\)
Phát biểu nào sau đây là đúng nhất khi nói về khái niệm gia tốc?
Cả A, B, C đều đúng
Một xe ôtô đi từ Ba La vào trung tâm Hà Nội có đồ thị v-t như hình vẽ:
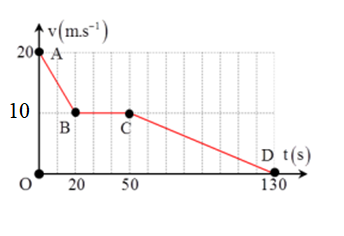
Quãng đường mà ôtô đi được là:
Ta có:
+ Trên đoạn \(A \to B\) xe chuyển động chậm dần đều với gia tốc: \({a_1} = \frac{{{v_B} - {v_A}}}{{\Delta t}} = \frac{{10 - 20}}{{20}} = - 0,5m/{s^2}\)
Quãng đường vật đi được: \({s_1} = 20t - 0,25{t^2} = 20.20 - 0,{25.20^2} = 300m\)
+ Trên đoạn \(B \to C\) xe chuyển động thẳng đều với vận tốc \(v = 10m/s\)
Quãng đường vật đi được: \({s_2} = vt = 10.30 = 300m\)
+ Trên đoạn \(C \to D\) xe chuyển động chậm dần đều với gia tốc:
\({a_3} = \frac{{0 - 10}}{{130 - 50}} = - 0,125m/s{}^2\)
Quãng đường vật đi được: \({s_3} = 10t - 0,0625{t^2} = 10.80 - 0,{0625.80^2} = 400m\)
Vậy quãng đường mà ôtô đi được là: \(s = {s_1} + {s_2} + {s_3} = 300 + 300 + 400 = 1000m\)
Trong công thức liên hệ giữa quãng đường đi được, vận tốc và gia tốc của chuyển động nhanh dần đều \({v^2} - v_0^2 = 2{\rm{as}}\), ta có các điều kiện nào sau đây?
Công thức \({v^2} - v_0^2 = 2{\rm{as}}\) chỉ đúng khi chuyển động là không đổi chiều. Với v > v0 => vật chuyển động theo chiều dương, chuyển động là nhanh dần nên a và v cùng chiều do vậy a > 0, quãng đường s là một đại lượng không âm
Một chất điểm chuyển động thẳng có đồ thị vận tốc - thời gian như hình vẽ. Trong suốt quá trình chuyển động, tốc độ trung bình là 9 m/s. Phương trình chuyển động của chất điểm khi đi từ B đến C là?
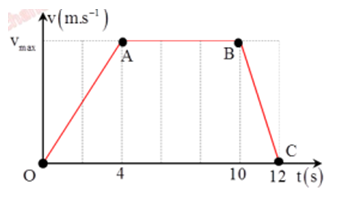
Ta có :
+ Tốc độ trung bình của vật : \({v_{tb}} = \dfrac{s}{t} = \dfrac{{\dfrac{1}{2}{v_{{\rm{max}}}}.4 + {v_{{\rm{max}}}}.6 + \dfrac{1}{2}{v_{{\rm{max}}}}.2}}{{12}} = 9 \to {v_{{\rm{max}}}} = 12m/s\)
+ Gia tốc của chất điểm khi chuyển động từ B đến C: \(a = \dfrac{{0 - 12}}{2} = - 6m/s\)
=> Phương trình chuyển động của chất điểm khi đi từ B đến C là: \(x = 96 + 12(t - 10) - 3{(t - 10)^2}\)
Ba vật chuyển động thẳng có đồ thị v - t như hình vẽ:
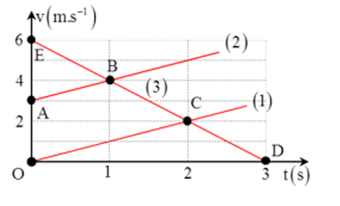
Sau bao nhiêu giây thì vật thứ 3 sẽ dừng lại?
Ta có vật dừng lại khi v = 0
Từ đồ thị, ta có: vật thứ 3 có vận tốc bằng không khi t = 3s
=> Sau 3s thì vật thứ 3 sẽ dừng lại
Phương trình chuyển động của một vật trên một đường thẳng có dạng \(x = 2{t^2} + 10t + 100(m;s)\).Thông tin nào sau đây là đúng?
Từ phương trình chuyển động ta có: \(\left\{ \begin{array}{l}{x_0} = 100m\\{v_0} = 10m/s\\a = 4m/{s^2}\end{array} \right.\)
=> Vật chuyển động nhanh dần đều với gia tốc \(a = 4{\rm{ }}m/{s^2}\)
Tọa độ lúc ban đầu của vật là \({x_0} = 100m\)
Vận tốc của vật tại thời điểm ban đầu: \({v_0} = 10m/s\)

