Phép chia hết và phép chia có dư

I. KIẾN THỨC CẦN NHỚ

- Phép chia hết và phép chia có dư:

- Số dư bé hơn số chia.

- Vận dụng phép chia hết và phép chia có dư vào giải toán.

Ví dụ:

II. CÁC DẠNG TOÁN

Dạng 1: Kiểm tra phép chia đó là phép chia hết hay phép chia có dư

Bước 1: Đặt tính phép chia theo hàng dọc.

Bước 2: Thực hiện phép chia

Bước 3: Kiểm tra số dư của phép chia, nếu số dư bằng $0$ thì đó là phép chia hết; nếu số dư khác $0$ thì đó là phép chia có dư.

Ví dụ: $64:2$ là phép chia hết hay phép chia có dư ?

Giải:

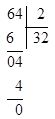
Ta thấy phép chia có số dư bằng $0$ nên $64:2$ là một phép chia hết.

Dạng 2: Toán đố

Bước 1: Đọc và phân tích đề, xác định các số đã cho và yêu cầu của bài toán.

Bước 2: Muốn tìm giá trị của một nhóm trong các nhóm bằng nhau thì ta thường sử dụng phép tính chia.

- Vận dụng tính chất của phép chia hết và phép chia có dư để trả lời các câu hỏi của bài toán.

Bước 3: Trình bày lời giải của bài toán.

Ví dụ: Một đoàn có $30$ người đi du lịch, nếu mỗi xe chỉ chở được $4$ người thì đoàn đó cần bao nhiêu xe như vậy?

Phương pháp giải:

- Để tìm được số xe để chở hết đoàn người đó thì ta cần kiểm tra $30$ gồm bao nhiêu nhóm $4$ bằng cách dùng phép tính chia.

 - Nếu phép chia có dư thì để đủ xe cho cả đoàn ta cần dùng thêm một xe nữa.

Cách giải:

Ta có: $30{\rm{ }}:{\rm{ }}4{\rm{ }} = {\rm{ }}7$ (dư $2$)

Vậy để chở được $30$ người thì cần số xe là:

$7{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}8$ (xe)

Đáp số: $8$ xe.

Dạng 3: Các tính chất của phép chia có dư.

Trong một phép chia có dư thì: