I. KIẾN THỨC CẦN NHỚ
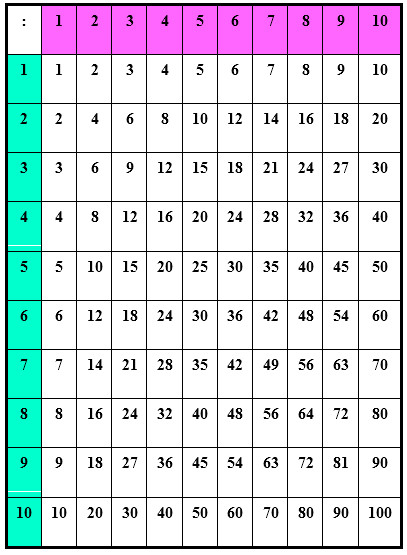
Bảng chia và cách sử dụng bảng chia để tra kết quả của một phép chia trong phạm vi ${\bf{100}}$
- Cột dọc đầu tiên tương ứng với số chia.
- Cột ngang đầu tiên tương ứng với thương.
II. CÁC DẠNG TOÁN
Dạng 1: Dùng bảng chia để tìm số thích hợp trong phép chia.
Áp dụng đúng cách tìm kết quả của phép chia dựa vào bảng chia vừa học.
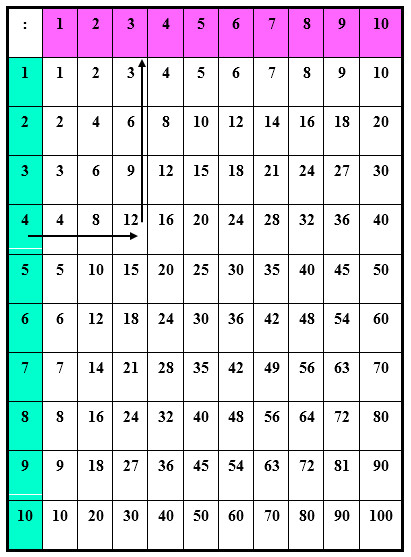
Ví dụ: Tìm kết quả của phép chia $12:4 = ?$
* Từ số $4$ ở cột một theo chiều mũi tên sang phải đến số $12$.
* Từ số $12$ theo chiều mũi tên lên hàng $1$ gặp số $3$
* Ta có: $12:4 = 3$
Tương tự: $12:3 = 4$
Dạng 2: Toán đố tìm một trong các phần bằng nhau của một số
Bước 1: Đọc và phân tích đề bài, xác định số đã cho, số cần tìm và dạng toán
Bước 2: Tìm cách giải cho bài toán.
Muốn tìm một trong các phần bằng nhau của một số thì ta lấy số đó chia cho số phần.
Bước 3: Trình bày lời giải.
Bước 4: Kiểm tra cách trình bày và kết quả vừa tìm được.
Ví dụ: Một bao gạo nặng \(45kg\), người bán hàng lấy ra \(\dfrac{1}{5}\) bao gạo đó.Hỏi người đó đã lấy ra bao nhiêu ki-lô-gam gạo ?
- Phân tích đề và tìm cách giải:
Muốn tìm \(\dfrac{1}{5}\) bao gạo bằng bao nhiêu ki-lô-gam thì cần lấy khối lượng bao gạo đã cho chia cho \(5\)
Giải:
Người bán hàng đã lấy ra số ki-lô-gam gạo là:
\(45:5 = 9\left( {kg} \right)\)
Đáp số: \(9kg\)
Dạng 3: Tìm yếu tố còn thiếu trong phép toán.
Muốn tìm số chia ta lấy số bị chia chia cho thương.
Muốn tìm số bị chia ta lấy thương nhân với số chia.
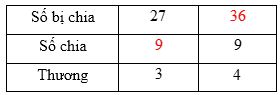
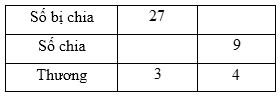
Ví dụ: Điền số còn thiếu vào bảng sau:
Giải:
Ta có: \(27:3 = 9\) và \(4 \times 9 = 36\) nên em điền các số vào ô trống như sau: