I. KIẾN THỨC CẦN NHỚ
- Bảng chia ${\bf{7}}$ và phép chia trong phạm vi ${\bf{7}}$
Xuất phát từ phép nhân $7$, ta có thể nhẩm được giá trị của phép chia \(7\):
Bảng chia \(7\):
\(\begin{array}{l}7:7 = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,42:7 = 6\\14:7 = 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,49:7 = 7\\21:7 = 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,56:7 = 8\\28:7 = 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,63:7 = 9\\35:7 = 5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,70:7 = 10\end{array}\)
- Tìm được giá trị \(\dfrac{{\bf{1}}}{{\bf{7}}}\) của một số hoặc một hình đơn giản:
+) Chia số ban đầu cho \(7\).
+) Chia hình đã cho thành \(7\) phần bằng nhau và tô màu một phần.
II. CÁC DẠNG TOÁN
Dạng 1: Tính nhẩm
Dựa vào bảng nhân và chia \(7\) đã học, nhẩm tính các kết quả của phép nhân, chia trong phạm vi \(7\)
Ví dụ: \(42:7\)
Giải:
Nhẩm \(7 \times 6 = 42\) nên \(42:7 = 6\)
Dạng 2: Toán đố
Bước 1: Đọc và phân tích đề bài, cho giá trị của một số nhóm bằng nhau, yêu cầu tìm giá trị của “mỗi”hoặc “một” nhóm.
Bước 2: Muốn tìm giá trị của một nhóm, ta lấy giá trị của các nhóm chia cho số nhóm.
Bước 3: Trình bày lời giải.
Bước 4: Kiểm tra cách trình bày và kết quả vừa tìm được.
Ví dụ: Một sợi dây dài \(56cm\) được cắt thành \(7\) đoạn bằng nhau. Mỗi đoạn dài bao nhiêu xăng-ti-mét ?
- Phân tích đề và tìm cách giải:
Muốn tìm độ dài một đoạn thẳng thì ta lấy độ dài của cả sợi dây đem chia cho \(7\)
Giải:
Mỗi đoạn dây dài số xăng-ti-mét là:
\(56:7 = 8\left( {cm} \right)\)
Đáp số: \(8cm\)
Dạng 3: Giá trị \(\dfrac{{\bf{1}}}{{\bf{7}}}\)
Muốn tìm $\dfrac{1}{7}$ của một số, ta cần chia số đó cho $7$.
Muốn tìm \(\dfrac{1}{7}\) của một hình thì cần chia hình đó thành \(7\) phần bằng nhau và tô một phần.
Ví dụ: Tô màu \(\dfrac{1}{7}\) số ô vuông dưới đây ?
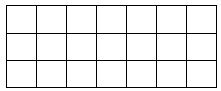
Giải:
Hình trên có \(21\) ô vuông.
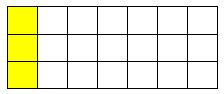
Ta có: \(21:7 = 3\)
Vậy để tô \(\dfrac{1}{7}\) số ô vuông ở hình trên thì em cần tô màu \(3\) ô vuông.
Dạng 4: Tính giá trị biểu thức
Muốn tính giá trị của biểu thức, ta cần ghi nhớ quy tắc chung:
+ Biểu thức có chứa nhân/chia và cộng trừ thì cần làm phép toán nhân/chia trước, sau đó đến các phép toán cộng/trừ.
+ Biểu thức chỉ có chứa phép nhân và phép chia thì ta thực hiện các phép toán theo thứ tự từ trái sang phải.
Ví dụ: Tính
\(\begin{array}{l}a)\,\,35:7 \times 3\\b)\,\,35 - 7:7\end{array}\)
Giải:
\(\begin{array}{l}a)\,\,35:7 \times 3 = 5 \times 3 = 15\\b)\,\,35 - 7:7 = 35 - 1 = 34\end{array}\)
Dạng 5: Tìm x
Muốn tìm thừa số chưa biết, ta lấy tích chia cho thừa số đã biết.
Ví dụ: Tìm \(x\), biết:
\(x \times 7 = 63\)
Giải:
\(x\) là thừa số trong phép nhân.
Muốn tìm thừa số ta lấy tích chia cho thừa số đã biết.
\(\begin{array}{l}x \times 7 = 63\\x\,\,\,\,\,\,\,\,\, = 63:7\\x\,\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,9\end{array}\)
Dạng 6: So sánh
Bước 1: Tính giá trị các biểu thức, phép tính.
Bước 2: So sánh và dùng dấu >; < hoặc = thích hợp.
Ví dụ: Phép toán có giá trị bé nhất là:
A. \(35:7\) B. \(42:6\) C. \(7 \times 0\)
Giải:
Tính giá trị của các phép toán:
\(\begin{array}{l}35:7 = 5\\42:6 = 7\\7 \times 0 = 0\end{array}\)
Vì \(7 > 5 > 0\) nên phép toán có giá trị nhỏ nhất là \(7 \times 0\) (Đáp án A)


