Tiên đề Euclid. Tính chất của các đường thẳng song song
Sách kết nối tri thức với cuộc sống
Cho hình vẽ sau:
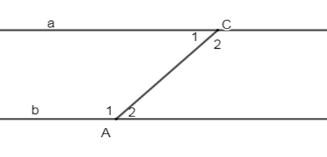
Biết \(a\,//\,b,\,\widehat {{A_1}} - \widehat {{C_1}} = {40^0}\). Tính \(\widehat {{A_2}},\,\widehat {{C_2}}\).
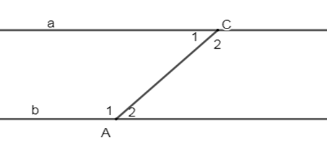
Vì \(a\,//\,b\left( {gt} \right) \Rightarrow \widehat {{A_1}} + \widehat {{C_1}} = {180^0}\) (2 góc trong cùng phía bù nhau)
Mà lại có:
\(\begin{array}{l}\widehat {{A_1}} - \widehat {{C_1}} = {40^0}\left( {gt} \right) \Rightarrow \widehat {{A_1}} = \left( {{{180}^0} + {{40}^0}} \right):2 = {110^0}\\ \Rightarrow \widehat {{C_1}} = {110^0} - {40^0} = {70^0}\end{array}\)
Vì $a\,//\,b\left( {gt} \right) \Rightarrow \left\{ \begin{array}{l}\widehat {{A_1}} = \widehat {{C_2}} = {110^0}\\\widehat {{C_1}} = \widehat {{A_2}} = {70^0}\end{array} \right.$(2 góc so le trong)
Vậy \(\widehat {{A_2}} = 70^\circ ;\,\widehat {{C_2}} = 110^\circ .\)
Cho hình vẽ sau:
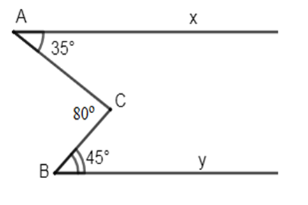
Biết \(\widehat {xAC} = {35^0},\,\widehat {CBy} = {45^0}\) và \(\widehat {ACB} = {80^0}.\) Khi đó chọn câu đúng.
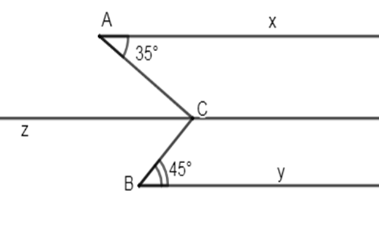
Kẻ \(Cz//{\rm{Ax}} \Rightarrow \widehat {xAC} = \widehat {ACz} = {35^0}\) (so le trong)
Ta có:
\(\widehat {ACz} + \widehat {zCB} = \widehat {ACB} \Rightarrow \widehat {zCB} = \widehat {ACB} - \widehat {ACz} = {80^0} - {35^0} = {45^0}\)
\( \Rightarrow \widehat {zCB} = \widehat {CBy}\left( { = {{45}^0}} \right)\)
Mà hai góc ở vị trí so le trong nên suy ra \(Cz//\,By\) (dấu hiệu nhận biết hai đường thẳng song song)
Ta có: \(\left\{ \begin{array}{l}Cz//\,Ax\left( {gt} \right)\\C{\rm{z}}//\,By\left( {cmt} \right)\end{array} \right. \Rightarrow Ax//\,By\) .
Cho hình vẽ sau, biết \(a//b\) và \(\widehat {{A_1}} = {100^0}\). Tính $\widehat {{B_1}},\widehat {{B_2}}$.
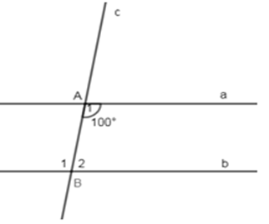
Vì \(a//b\left( {gt} \right) \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\, = {100^0}\) (hai góc so le trong)
Lại có: \(\widehat {{A_1}} + \widehat {{B_2}} = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow \widehat {{B_2}} = {180^0} - \widehat {{B_1}} = {180^0} - {100^0} = {80^0}.\)
Cho hình vẽ sau
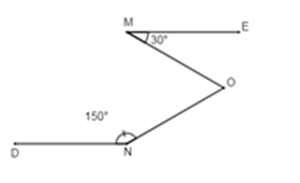
Biết \(ME//N{\rm{D}},\,\widehat {EM{\rm{O}}} = {30^0},\,\widehat {DNO} = {150^0}\). Tính \(\widehat {MON}\) .
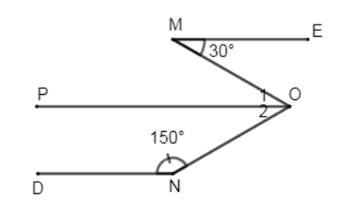
Kẻ \(OP\) sao cho \(OP//ME.\)
Ta có: \(OP//\,ME \Rightarrow \widehat M = \widehat {{O_1}} = {30^0}\) (2 góc so le trong)
Ta có: \(\left\{ \begin{array}{l}OP\,//\,ME\\ME\,//\,DN\end{array} \right.\left( {gt} \right) \Rightarrow PO\,//\,DN\)
\( \Rightarrow \widehat {{O_2}} + \widehat N = {180^0}\) (2 góc trong cùng phía bù nhau)
\( \Rightarrow \widehat {{O_2}} = {180^0} - \widehat N = {180^0} - {150^0} = {30^0}\)
Ta có: \(\widehat {MON} = \widehat {{O_1}} + \widehat {{O_2}} = {30^0} + {30^0} = {60^0}\)
Vậy \(\widehat {MON} = 60^\circ .\)
Cho hình vẽ sau:
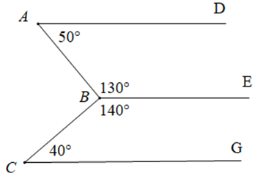
Chọn câu đúng.
Vì \(\widehat A + \widehat {ABE} = 50^\circ + 130^\circ = 180^\circ \) mà hai góc ở vị trí trong cùng phía nên $AD//BE.$
Vì \(\widehat {CBE} + \widehat C = 140^\circ + 40^\circ = 180^\circ \) mà hai góc ở vị trí trong cùng phía nên \(BE//CG.\)
Vậy cả A, B đều đúng.
Cho hình 21 biết \(a \bot c\) và \(b \bot c\), đồng thời \(2\widehat {{C_4}} = 3\widehat {{D_5}}.\) Tìm số đo \(\widehat {{D_5}}.\)
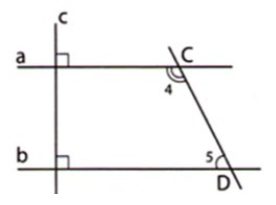
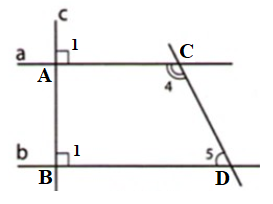
Theo đề bài: \(a \bot c\) và \(b \bot c\) nên \(\widehat {{A_1}} = \,\widehat {{B_1}} = {90^o}\), mà hai góc này ở vị trí đồng vị nên \(a//b.\)
Vì \(a//b\,\,(cmt)\) nên \(\widehat {{C_4}} + \widehat {{D_5}} = {180^o}\) (hai góc trong cùng phía bù nhau) (1)
Lại có: \(2\widehat {{C_4}} = 3\widehat {{D_5}}\) suy ra \(\widehat {{C_4}} = \dfrac{{3\widehat {{D_5}}}}{2}\) (2)
Thay (2) vào (1) ta được:
\(\begin{array}{l}\dfrac{{3\widehat {{D_5}}}}{2} + \widehat {{D_5}} = {180^o}\\ \Rightarrow \dfrac{5}{2}\widehat {{D_5}} = {180^o}\\ \Rightarrow \widehat {{D_5}} = {180^o}:\dfrac{5}{2} = {72^0}\end{array}\)
Vậy \(\widehat {{D_5}} = {72^o}\).

