Hai đường thẳng song song và dấu hiệu nhận biết
Sách kết nối tri thức với cuộc sống
Cho hình vẽ sau:
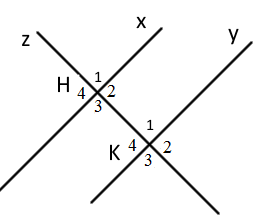
Em hãy chọn phát biểu đúng trong các phát biểu sau:
\(\widehat {{H_1}}\) và \(\widehat {{K_1}}\) là hai góc so le trong (sai, vì đó là 2 góc đồng vị, loại đáp án A)
\(\widehat {{H_4}}\) và \(\widehat {{K_4}}\) là hai góc đồng vị (đúng, chọn B)
\(\widehat {{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài (sai, vì đó là 2 góc trong cùng phía, loại đáp án C)
\(\widehat {{H_4}}\) và \(\widehat {{K_2}}\) là hai góc so le trong (sai, vì đó là 2 góc so le ngoài, loại đáp án D)
Tính giá trị \(x;y;z;t\) trên hình sau:
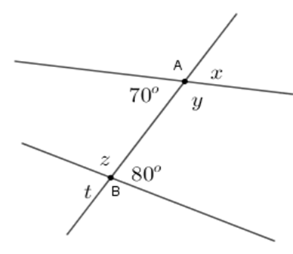
Ta có \(x = {70^0}\) (tính chất hai góc đối đỉnh)
\(y + {70^o} = {180^o} \Rightarrow y = {110^o}\) (hai góc kề bù)
Tương tự ta có \(t = {80^o};\,z = {100^o}\)
Vậy $x = {70^o};y = {110^0};z = {100^o};t = {80^o}.$
Biết một cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\). Tính số đo của cặp góc so le trong còn lại.

Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\( \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {35^0} = {145^0}\)
Ta có: \(\widehat {{A_3}}\) và \(\widehat {{B_2}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\) là 2 cặp góc so le trong
Mặt khác, đường thẳng d cắt 2 đường thẳng x và y tạo thành 1 cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\) nên cặp góc so le trong còn lại cũng bằng nhau
\( \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {145^0}.\)
Cho hình vẽ sau:
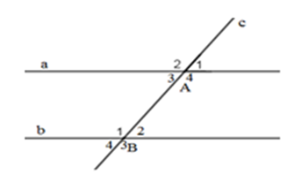
Biết \(\widehat {{A_3}} = \widehat {{B_2}} = {30^0}\). Tính số đo góc \({A_4}\) và góc \({B_1}.\)
Cặp góc so le trong còn lại là: \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\).
Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {30^0} = {150^0}\\ \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {150^0}\end{array}\)

