Theo định luật I Niu-tơn thì?
Định luật I - Niutơn: Nếu một vật không chịu tác dụng của lực nào hoặc chịu tác dụng của các lực có hợp lực bằng không, thì nó giữ nguyên trạng thái đứng yên hoặc chuyển động thẳng đều.
Biểu thức nào sau đây diễn tả biểu thức của định luật II - Niutơn?
Định luật II - Niutơn: Véctơ gia tốc của một vật luôn cùng hướng với lực tác dụng lên vật. Độ lớn của véctơ gia tốc tỉ lệ thuận với độ lớn của véctơ lực tác dụng lên vật và tỉ lệ nghịch với khối lượng của vật.
\(\overrightarrow a = \dfrac{{\overrightarrow F }}{m}\) hay \(\overrightarrow F = m\overrightarrow a \)
Chọn phát biểu đúng về định luật III Niutơn
Định luật III - Niutơn: Khi vật A tác dụng lên vật B một lực, thì vật B cũng tác dụng trở lại vật A một lực. Hai lực này là hai lực trực đối: \({\overrightarrow F _{AB}} = - {\overrightarrow F _{BA}}\)
Theo định luật III Niu-tơn thì lực và phản lực?
Một trong hai lực tương tác giữa hai vật gọi là lực tác dụng còn lực kia gọi là phản lực.
Đặc điểm của lực và phản lực :
+ Lực và phản lực luôn luôn xuất hiện (hoặc mất đi) đồng thời.
+ Lực và phản lực có cùng giá, cùng độ lớn nhưng ngược chiều.
Hai lực có đặc điểm như vậy gọi là hai lực trực đối.
+ Lực và phản lực không cân bằng nhau vì chúng đặt vào hai vật khác nhau.
Vật nào sau đây chuyển động theo quán tính?
Vật chuyển theo quán tính là vật chuyển động khi tất cả các lực tác dụng lên vật mất đi
Khi nói về một vật chịu tác dụng của lực, phát biểu nào sau đây đúng?
A, B, D- sai
C - đúng
Hai lực trực đối cân bằng là:
Hai lực trực đối cân bằng là hai lực có cùng độ lớn, cùng phương, ngược chiều tác dụng vào hai vật khác nhau
Cặp “lực và phản lực” trong định luật III Niutơn:
Cặp “lực và phản lực” trong định luật III Niutơn là hai lực trực đối cân bằng có cùng độ lớn, cùng phương, ngược chiều tác dụng vào hai vật khác nhau
Đại lượng đặc trưng cho mức quán tính của một vật là:
Khối lượng của vật là đại lượng đặc trưng cho mức quán tính của vật.
Hai xe A (mA) và B (mB) đang chuyển động với cùng một vận tốc thì tắt máy và cùng chịu tác dụng của một lực hãm F như nhau. Sau khi bị hãm, xe A còn đi thêm được một đoạn sA, xe B đi thêm một đoạn là sB < sA. Điều nào sau đây là đúng khi so sánh khối lượng của hai xe?
Chọn chiều dương trùng chiều chuyển động của xe
Lực hãm xe có độ lớn \(F\)
+ Theo định luật II Niutơn, ta có gia tốc của các xe:
\({a_A} = \dfrac{{ - F}}{{{m_A}}};{a_B} = \dfrac{{ - F}}{{{m_B}}}\) (1)
(do các xe chuyển động chậm dần đều, lực hãm có chiều ngược chiều chuyển động)
+ Ta có: \({v^2} - v_0^2 = 2{\rm{as}}\)
=> Quãng đường xe A và xe B đi được thêm là:
\({s_A} = - \dfrac{{v_0^2}}{{2{a_A}}};{s_B} = - \dfrac{{v_0^2}}{{2{a_B}}}\) (2)
Theo đầu bài, ta có:
\(\begin{array}{*{20}{l}}{{s_B} < {s_A} \leftrightarrow - \dfrac{{v_0^2}}{{2{a_B}}} < - \dfrac{{v_0^2}}{{2{a_A}}}}\\{ \leftrightarrow \dfrac{{v_0^2}}{{2{a_B}}} > \dfrac{{v_0^2}}{{2{a_A}}} \to {a_A} > {a_B}}\end{array}\)
Kết hợp với (1), ta được:
\(\begin{array}{l} \to \dfrac{{ - F}}{{{m_A}}} > \dfrac{{ - F}}{{{m_B}}}\\ \leftrightarrow \dfrac{1}{{{m_A}}} < \dfrac{1}{{{m_B}}}\\ \to {m_B} < {m_A}\end{array}\)
Một ôtô có khối lượng 1 tấn đang chuyển động với v = 54km/h thì hãm phanh, chuyển động chậm dần đều. Biết lực hãm 3000N. Xác định quãng đường xe đi được cho đến khi dừng lại?
Ta có: \(v = 54km/h = 15m/s\)
+ Chọn chiều (+) là chiều chuyển động, gốc thời gian lúc bắt đầu hãm phanh.
Theo định luật II - Niutơn, ta có: \(\overrightarrow a = \frac{{\overrightarrow F }}{m} \to a = - \frac{F}{m} = - \frac{{3000}}{{1000}} = - 3m/{s^2}\)
+ Mặt khác, ta có:
\(\begin{array}{l}{v^2} - v_0^2 = 2{\rm{as}} \leftrightarrow 0 - {15^2} = 2.( - 3)s\\ \to {\rm{s}} = {\rm{37,5m}}\end{array}\)
Một quả bóng m = 0,4kg đang nằm yên trên mặt đất. Một cầu thủ đá bóng với lực 300N. Thời gian chân tác dụng vào quả bóng là 0,015s. Tính tốc độ của quả bóng lúc bay đi.
+ Theo định luật II Niutơn, ta có: \(a = \frac{F}{m} = 750m/{s^2}\)
+ Chọn gốc thời gian là lúc chân cầu thủ chạm vào bóng
+ Phương trình vận tốc của vật: \(v = {v_0} + at = 0 + 750.0,015 = 11,25\,m/s\)
Cho viên bi $A$ chuyển động tới va chạm vào bi $B$ đang đứng yên, ${v_A} = {\rm{ }}2m/s$ sau va chạm bi $A$ tiếp tục chuyển động theo phương cũ với $v = 1m/s$, thời gian xảy ra va chạm là $0,4s$. Tính gia tốc của viên bi thứ $2$ , biết ${m_A} = {\rm{ }}200g,{\rm{ }}{m_B} = {\rm{ }}100g$.
Ta xét chuyển động của xe $A$ có vận tốc trước khi va chạm là \({v_A} = 2m/s\), sau va chạm xe A có vận tốc là \(v = 1m/s\)
Áp dụng biểu thức xác định gia tốc: \(a = \dfrac{{{v_2} - {v_1}}}{{\Delta t}} = \dfrac{{1 - 2}}{{0,4}} = - 2,5m/s\)
+ Theo định luật $III$ Niu-tơn: \({\overrightarrow F _{AB}} = - {\overrightarrow F _{BA}}\)
+ Theo định luật $II$, ta có: $F = ma$
\(\begin{array}{l} \to {|F_{AB}|} = {|F_{BA}|} \leftrightarrow {m_A}{|a_A|} = {m_B}{a_B}\\ \to {a_B} = \dfrac{{{m_A}{|a_A|}}}{{{m_B}}} = \dfrac{{0,2.2,5}}{{0,1}} = 5m/{s^2}\end{array}\)
Một vật đang đứng yên, được truyền 1 lực F thì sau 5s vật này tăng 2m/s. Nếu giữ nguyên hướng của lực mà tăng gấp 2 lần độ lớn lực F vào vật thì sau 8s, vận tốc của vật tăng bao nhiêu?
Ta có:
+ Ban đầu: \({a_1} = \frac{{\Delta {v_1}}}{{\Delta t}} = \frac{2}{5} = 0,4m/{s^2}\)
Mặt khác, ta có: \({F_1} = m{a_1} = 0,4m\)
+ Khi tăng \(F' = 2.{F_1} = {\rm{2}}{\rm{.0,4m}} = 0,8m\)
\( \to {{\rm{a}}_2} = \frac{{0,8m}}{m} = 0,8m/{s^2}\)
Lại có: \({a_2} = \frac{{\Delta {v_2}}}{{\Delta t}} = \frac{{\Delta {v_2}}}{8} = 0,8m/{s^2} \to \Delta {v_2} = 6,4m/s\)
Một ôtô có khối lưọng $500kg$ đang chuyển động thẳng đều thì hãm phanh chuyển động chậm dần đều trong $2s$ cuối cùng đi được $1,8 m$. Hỏi lực hãm phanh tác dụng lên ôtô có độ lớn là bao nhiêu?
+ Ta có:
\({v^2} - v_0^2 = 2{\rm{as}} \to - v_0^2 = 2{\rm{as}} = 3,6{\rm{a }}(1)\)
Mặt khác: \(a = \dfrac{{v - {v_0}}}{{\Delta t}} \to - {v_0} = at = 2a{\rm{ (2)}}\)
Từ (1) và (2) ta suy ra: \(a = - 0,9{\rm{ }}m/{s^2}\)
+ Lực hãm phanh tác dụng lên ôtô: \(F = m.a{\rm{ }} = - 450N\)
Vật trượt từ đỉnh mặt phẳng nghiêng nhãn dài \(l = 10m\), góc nghiêng \(\alpha = {30^0}\) . Hỏi vật tiếp tục chuyển động trên mặt phẳng ngang bao lâu khi xuống hết mặt phẳng nghiêng, biết hệ số ma sát với mặt phẳng ngang là \(\mu = 0,1\).
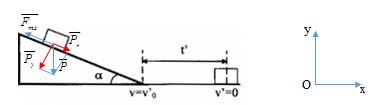
+ Gắn hệ trục tọa độ như hình vẽ
+ Viết phương trình định luật II – Niuton cho vật ta được:
\(\overrightarrow P + \overrightarrow {{F_{ms}}} = m\overrightarrow a \) (1)
+ Chiếu (1) lên các phương ta được:
Ox: \({P_x} - {F_{ms}} = ma \to a = \dfrac{{{P_x} - {F_{ms}}}}{m} = \dfrac{{P\sin \alpha - \mu P\cos \alpha }}{m} = g\sin \alpha - \mu g\cos \alpha \)
+ Vì mặt phẳng nghiêng nhẵn nên hệ số ma sát bằng \(0\), do đó: \(a = g.\sin \alpha = 10.\sin {30^0} = 5m/{s^2}\)
+ Vận tốc của vật ở cuối mặt phẳng nghiêng là: \(v = \sqrt {2al} = \sqrt {2.5.10} = 10m/s\)
+ Gia tốc của vật trên mặt phẳng ngang là: \(a' = - \dfrac{{{F_{ms}}}}{m} = - \dfrac{{\mu mg}}{m} = - \mu g = - 0,1.10 = - 1m/{s^2}\)
+ Thời gian vật đi trên mặt phẳng ngang là: \(t' = \dfrac{{v' - v{'_0}}}{{a'}} = \dfrac{{0 - v}}{{a'}}\) (do vật dừng lại nên \(v' = 0\) )
Ta suy ra: \(t' = \dfrac{{ - v}}{{a'}} = \dfrac{{ - 10}}{{ - 1}} = 10s\)
Hai xe lăn có khối lượng \({m_1} = 2kg;{m_2} = 3kg\) được đặt trên ray thẳng nằm ngang. Cho hai xe tương tác với nhau bằng cách đặt một lò xo được nén ở giữa chúng rồi nối bằng dây chỉ. Sau khi đốt dây chỉ đứt, xe một thu được vận tốc 4 m/s. Tốc độ mà xe hai thu được là:
Gọi t - thời gian tương tác giữa hai xe
Độ lớn gia tốc của mỗi xe lần lượt là: \({a_1} = \frac{{{v_1}}}{t};{a_2} = \frac{{{v_2}}}{t}\)
Theo định luật III - Niutơn, ta có lực do xe 1 tác dụng vào xe 2 và lực do xe 2 tác dụng vào xe 1 bằng nhau về độ lớn
Áp dụng định luật II Niutơn, ta có:
\(\begin{array}{l}{m_1}{a_1} = {m_2}{a_2} \leftrightarrow {m_1}\frac{{{v_1}}}{t} = {m_2}\frac{{{v_2}}}{t}\\ \to {m_1}{v_1} = {m_2}{v_2}\\ \to {v_2} = \frac{{{m_1}{v_1}}}{{{m_2}}} = \frac{{2.4}}{3} = \frac{8}{3} \approx 2,67m/s\end{array}\)
Vật được thả trượt trên mặt phẳng nghiêng dài AB = 2,5m, góc nghiêng α = 300 như hình vẽ, có hệ số ma sát µ = 0,2. Cho g = 10m/s2. Tính vận tốc vật đạt được ở chân mặt phẳng nghiêng và thời gian vật đi hết mặt phẳng nghiêng
Áp dụng định luật 2 Niu tơn ta có:
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{{{F}_{ms}}}=m\overrightarrow{a}\)
Chiếu lên Oy ta được: N = Py = mgcosα
Chiếu lên Ox ta được:
Px – Fms = ma
mgsinα - µmgcosα = ma
a = gsinα - µgcosα = 3,27m/s2
v0 = 0, S = 2,5m
Thời gian đi hết mặt phẳng nghiêng : S = 0,5at2 =2,5m --> t = 1,24s
Vận tốc ở chân mặt phẳng nghiêng: v = at = 4,05m/s
Xe lăn 1 có khối lượng m1 = 400g có gắn một lò xo. Xe lăn 2 có khối lượng m2. Ta cho hai xe áp gần nhau bằng cách buộc dây để nén lò xo (hình 16.6). Khi ta đốt dây buộc, lò xo dãn ra và sau một thời gian Δt rất ngắn, hai xe đi về hai phía ngược nhau với tốc độ v1 = 1,5m/s; v2 = 1m/s. Tính m2 (bỏ qua ảnh hưởng của ma sát trong thời gian Δt).
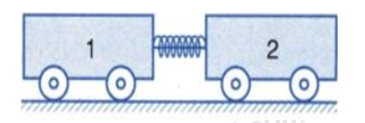
Gọi \(\overrightarrow {{F_{12}}\;} \) là lực mà thông qua lò xo, xe (1) tác dụng lên xe (2).
Theo định luật II Niuton: \({F_{12}} = {m_2}.{a_2} = {m_2}.\dfrac{{\Delta {v_2}}}{{\Delta t}} = {m_2}.\dfrac{{{v_2} - 0}}{{\Delta t}}\,\,\,\,\,\left( 1 \right)\)
Gọi \(\overrightarrow {{F_{21}}\;} \) là lực mà thông qua lò xo, xe (2) tác dụng lên xe (1).
Theo định luật II Niuton: \({F_{21}} = {m_1}.{a_1} = {m_1}.\dfrac{{\Delta {v_1}}}{{\Delta t}} = {m_1}.\dfrac{{{v_1} - 0}}{{\Delta t}}\,\,\,\,\,\left( 2 \right)\)
Theo định luật III Niuton, về độ lớn: F12 = F21 (3)
Từ (1), (2) và (3) suy ra:
\({m_2}.\dfrac{{{v_2}}}{{\Delta t}}\, = {m_1}.\dfrac{{{v_1}}}{{\Delta t}} \Rightarrow {m_2} = \dfrac{{{v_1}}}{{{v_2}}}.{m_1} = \dfrac{{1,5}}{1}.400 = 600g\)
Vậy khối lượng xe lăn (2) là m2 = 600g.
Cho 2 chất điểm A và B chuyển động trên cùng đường thẳng nằm ngang đến va chạm với nhau. Biết chất điểm A có khối lượng lớn hơn chất điểm B. Khi xảy ra va chạm thì:
Theo định luật III Niuton ta có:
\({F_{AB}} = {F_{BA}} \Leftrightarrow {m_B}{a_B} = {m_A}{a_A}\)
Mà \({m_A} > {m_B} \Rightarrow {a_B} > {a_A}\)